 |
Центральные кривые второго порядка
|
|
|
|
Рассмотрим уравнение кривой второго порядка без члена с произведением х и у
 (1-25)
(1-25)
Пологая, что А ≠ 0 и С ≠ 0 и дополняя до полных квадратов получим:
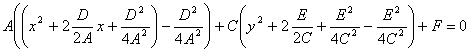
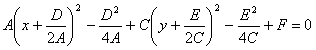
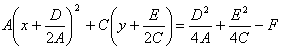
Полагая
 (1-26)
(1-26)
имеем:
 (1-27)
(1-27)
Таким образом точка О'(х0, у0) представляет собой центр симметрии кривой (1-27) (вспомним окружность).
Параллельные осям координат Оx и Оy прямые у = у0 и х = х0
являются осями симметрии кривой (1-15).
И если предположить, что х0 = 0 и у0 = 0, то наше уравнение примет вид:
 (1-28)
(1-28)
Кривая второго порядка (1-28) называется эллипсом (точнее принадлежит эллиптическому типу), если коэффициенты А и С имеют одинаковые знаки.
Т.е. А▪С > 0 (1-29)
Для определённости предположим А > 0 и С > 0
Возможны три случая:
1) При Δ › 0 мы имеем действительный эллипс
 (1-30)
(1-30)
это каноническое уравнение эллипса
где 
 (1-31)
(1-31)

Рис. 1.21. Эллипс
2) При Δ = 0, кривая (1-28) вырождается в точку. Это случай вырожденного эллипса.
3) При Δ ‹ 0, кривая (1-28) не имеет действительных точек, и её условно называют мнимым эллипсом.
Кривая второго порядка (1-28) называется гиперболой (точнее, кривой гиперболического типа), если коэффициенты А и С имеют противоположные знаки, т.е. A•С ‹ 0.
Предположим А › 0, тогда С ‹ 0
Возможны три случая:
1) Δ › 0, имеем гиперболу  (1-32)
(1-32)
– каноническое уравнение гиперболы,
здесь:  - действительная полуось,
- действительная полуось,  - мнимая полуось.
- мнимая полуось.

Рис. 1.22. Гипербола
 - асимптоты гиперболы.
- асимптоты гиперболы.
2) Δ = 0, получаем пару пересекающихся прямых (вырождённая гипербола)

3) Δ ‹ 0, получаем гиперболу

(1-33)
с полуосями  и
и  ;
;
Если а′ = а и b′ = b, то гиперболы (1-32) и (1-33) называются спряжёнными.
Пример: определить вид и расположение кривой
. 
Дополняя до полных квадратов имеем
|
|
|
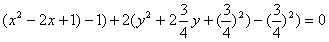
 откуда
откуда
 следовательно, это эллипс с центром в точке
следовательно, это эллипс с центром в точке
 ,
,  .
.
Билет 22.
Классификация кривых параболического типа.
Если:
a.  , то общее уравнение
, то общее уравнение  задает кривую параболического типа. Выделяя полный квадрат имеем:
задает кривую параболического типа. Выделяя полный квадрат имеем:
 .Обозначим:
.Обозначим:  имеем:
имеем:
 - канонический вид параболы.
- канонический вид параболы.
b.  , то
, то  - кривая параболического типа. Выделяя полный квадрат имеем:
- кривая параболического типа. Выделяя полный квадрат имеем:
 .Обозначим:
.Обозначим:  - имеем:
- имеем:
 - канонический вид параболы.
- канонический вид параболы.
Билет 23
Центральные поверхности второго порядка: эллипсоиды, гиперболоиды, конус. Канонические уравнения. Исследования по сечению.
1. Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид
a11х2 + а22у2 + a33z2 + а44 = 0 (2)
Так как инвариант I3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2), равно a11 • а22 • a33, то коэффициенты a11,а22, a33 удовлетворяют условию:
Возможны следующие случаи:
Д 1°. Коэффициенты a11,а22, a33 одного знака, а коэффициент а44 отличен от нуля. В этом случае поверхность S называется эллипсоидом.
Если коэффициенты a11,а22, a33, а44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом.
Если знак коэффициентов a11,а22, a33 противоположен знаку коэффициента а44, то поверхность S называется вещественным эллипсоидом. В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид.
Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа

положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме:
|
|
|
Каноническое уравнение:

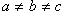 - трехосный эллипсоид;
- трехосный эллипсоид;
 - эллипсоид вращения вокруг оси Oz;
- эллипсоид вращения вокруг оси Oz;
 - эллипсоид вращения вокруг оси Oy;
- эллипсоид вращения вокруг оси Oy;
 - эллипсоид вращения вокруг оси Ox;
- эллипсоид вращения вокруг оси Ox;
Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. называются его главными осями.
Д 2°. Из четырех коэффициентов a11,а22, a33, а44 два одного знака, а два других—противоположного. В этом случае поверхность S называется однополостным гиперболоидом.
Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11 > 0, а22 > 0, a33 < 0, а44 < 0. Тогда числа
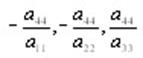
положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:
Каноническое уравнение:

a = b - однополостный гиперболоид вращения вокруг оси Oz.
Горловой эллипс: 
Асимптотический конус: 
Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).
Уравнение (4) называется каноническим уравнением однополостного гиперболоида.
Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу и Oz называются его главными осями.
Д 3°. Знак одного из первых трех коэффициентов a11,а22, a33, а44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом.
Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a11 < 0, а22 < 0, a33 > 0, а44 < 0. Тогда:

Обозначим эти числа соответственно через a2, b2, с2. После несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:
Каноническое уравнение:

a = b - двуполостный гиперболоид вращения вокруг оси Oz.
Асимптотический конус:

Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо  .
.
Если двуполостный гиперболоид задан своим каноническим
уравнением, то оси Ох, Оу и Оz называются его главными осями.
Д 4°. Коэффициент а44 равен нулю. В этом случае поверхность S называется конусом второго порядка.
Если коэффициенты a11, а22, a33 одного знака, то левая часть (2) обращается в нуль (а44 = 0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называется мнимым конусом второго порядка. Если коэффициенты a11, а22, a33 имеют разные знаки, то поверхность S является вещественным конусом второго порядка.
|
|
|
Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности,
a11 > o, а22 > 0, a33 < 0. Обозначим

соответственно через а2, b2, с2. Тогда уравнение (2) можно записать в виде:
Каноническое уравнение:

a = b - конус вращения (прямой круговой).
Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).
Билет 24.
Параболоиды и цилиндры второго порядка. Канонический вид и исследование посечению.
Эллиптический параболоид (рис. 4.22)
Каноническое уравнение: 
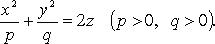
p = q - параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо  .
.

Гиперболический параболоид (рис. 4.23)
: 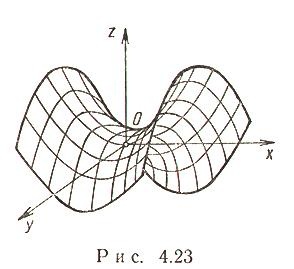
Каноническое уравнение 
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Билет 25.
Прямоугольная матрица. Сложение и умножение матрицы на число.
Операции над матрицами
|
|
|


