 |
Теорема (разложение определителя по строке или столбцу).
|
|
|
|
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = a i 1 A i 1 + a i 2 A i 2 +... + a i n A i n (i = 
)
или j- го столбца
d = a 1 j A 1 j + a 2 j A 2 j +... + a n j A n j (j = ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример 2.4. Не вычисляя определителя 
, показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель 
, равный исходному. Если из третьей строки также вычесть первую, то получится определитель 
, в котором две строки пропорциональны. Такой определитель равен нулю.
Определитель второго порядка
Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 
Примеры определителей второго порядка: 
Определитель третьего порядка
Определителем третьего порядка называется следующее выражение: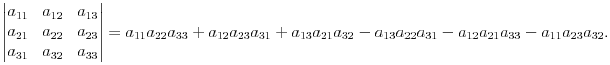 
Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. 
Примеры определителей третьего порядка: 
|
|
|
Билет 28.
Операция транспонирование матрицы и ее свойства. Определитель транспонированной матрицы.
Транспонирование матриц. Пусть 
. Матрица 
называется транспонированной к матрице A, если 
Транспонированная матрица также обозначается символами 
и 
.
Заметим, что при транспонировании матрицы её строки становятся столбцами матрицы 
, с теми же номерами, а столбцы - строками.
Теорема 2.4. Операция транспонирования матриц обладает следующими свойствами:
1) 
;
2) 
, для любого действительного числа 
;
3) 
;
4) 
, для любых матриц A и B, для которых имеют смысл левые части равенств.
Свойства 1), 2), 4) непосредственно вытекают из определения.
Приведём доказательство свойства 3). Пусть и 
, при таком согласовании размеров матриц A и B произведения AB и 
существуют, при этом размеры 
и совпадают и равны 
. Пусть 
- элемент матрицы AB в позиции (i,j), 
- элемент матрицы , - элемент матрицы в позиции (i,j).
что доказывает справедливость свойства 3).
Билет 29.
Свойства линейности определителя (10 штук). Операции над столбцами и строками не меняющие определитель.
ОПРЕДЕЛИТЕЛИ
Каждой квадратной матрице А соответствует число, которое называется ее определителем, или детерминантом, и обозначается | А |, det А, или 
. Определителем, или детерминантом, n -го порядка служит число, записываемое в виде квадратной таблицы
det А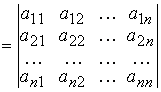 
и равное алгебраической сумме n! произведений вида 
.
Итак, det А 
,
где суммирование распространено на все перестановки из чисел 1, 2,..., n. Здесь 
– число инверсий в перестановке 
. Говорят, что числа 
и 
образуют инверсию в перестановке , если большее из чисел и расположено левее меньшего.
Например, для n 
2
,
для n 3
Правило вычисления определителя 
равносильно правилу треугольников (правилу Саррюса), которое схематически можно записать как
|
|
|
