 |
Умножение матрицы на число
|
|
|
|
Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен
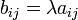
Свойства умножения матриц на число
1. 1*A = A;
2. (Λβ)A = Λ(βA)
3. (Λ+β)A = ΛA + βA
4. Λ(A+B) = ΛA + ΛB
Сложение матриц
Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен
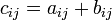
Свойства сложения матриц
5.коммутативность; (Коммутативная операция — это бинарная операция 
, обладающая коммутативностью (от позднелат. commutativus — «меняющийся»), то есть переместительностью:
для любых элементов 
.)
6.ассоциативность;(свойство любой операции , такое что для неё выполняется равенство:
для любых элементов 
.
Например, для умножения: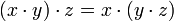 
.
7.сложение с нулевой матрицей;
8.существование противоположной матрицы;
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров MxN образуют линейное пространство над полем P(полем всех действительных или комплексных чисел), поэтому каждая матрица является и вектором этого пространства.
Умножение матриц
Умножение матриц (обозначение: AB, реже со знаком умножения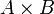 
) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность 
, B — 
, то размерность их произведения AB = C есть 
.
|
|
|
Свойства умножения матриц
1.ассоциативность;
2.произведение не коммутативно;
3.произведение коммутативно в случае умножения с единичной матрицей;
4.(ΛA)B = Λ(AB) = A(ΛB);
Билет 26.
Умножение прямоугольной матрицы и его свойства.
Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц.
Определение
Пусть даны две прямоугольные матрицы A и B размерности и 
соответственно:
Тогда матрица C размерностью 
называется их произведением:
где:
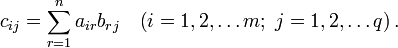
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
Следует заметить, что из существования произведения AB вовсе не следует существование произведения BA.
Свойства
Сочетательное свойство:
Распределительное свойство:
.
Произведение матрицы на единичную матрицу 
подходящего порядка равно самой матрице:
Произведение матрицы на нулевую матрицу 
подходящей размерности равно нулевой матрице:
Если 
и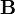 
— квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств.
Умножение матриц в целом некоммутативно:
Если 
, то матрицы и 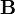называются перестановочными или коммутирующими между собой.
Билет 27.
Перестановки n-чисел. Четные и нечетные перестановки. Определение определителя.
Определители
Перестановкой чисел 1, 2,..., n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12...n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
|
|
|
Перестановка называется четной (или нечетной ), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 
обозначает подстановку, в которой 3 переходит в 4, 1 ® 2, 2 ® 1, 4 ® 3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 
,т.е. с натуральным расположением чисел в верхней строке.
Пусть нам дана квадратная матрица порядка n
. (4.3)
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
, (4.4)
где индексы q 1, q 2,..., q n составляют некоторую перестановку из чисел
1, 2,..., n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1) q, где q - число инверсий в перестановке вторых индексов элементов.
Определителем n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 
или det A= 
(детерминант, или определитель, матрицы А).
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
|
|
|
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a i j = b j + c j (j= 
), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b j, в другом - из элементов c j.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором M i j элемента a i j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента a i j определителя d называется его минор M i j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента a i jбудем обозначать A i j. Таким образом, A i j = (-1) i + j M i j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
|
|
|
