 |
Расстояние от точки до прямой в пространстве
|
|
|
|
Расстоянием от точки до прямой в пространстве называется длина перпендикуляра, опущенного из данной точки на прямую.

|M1M0×a|=|M1M0|•|a|•sinφ. sinφ=d/|M1M0|, следовательно, d=|M1M0|•sinφ. Тогда в силу первого равенства |M1M0×a|=d•|a|. d=|M1M0×a|/|a|. Так как относительно ПДСК вектор M1M0={x0-x1, y0-y1, z0-z1}, a={a, b, c}, то


Билет 15.
Расстояние между скрещивающимися прямыми, пересечение двух прямых.
Расстояние между скрещивающимися прямыми. Свойства
Теорема
Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
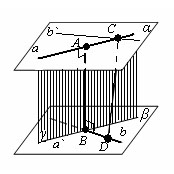
Доказательство
Пусть a и b – данные скрещивающиеся прямые. Проведем через них параллельные плоскости α и β. Прямые, пересекающие прямую a и перпендикулярные плоскости α, лежат в одной плоскости (γ). Эта плоскость пересекает плоскость β по прямой a`, параллельной a. Пусть B – точка пересечения прямых a` и b. Тогда прямая AB, перпендикулярная плоскости α, перпендикулярна и плоскости β, так как β параллельна α. Отрезок AB – общий перпендикуляр плоскостей α и β, а значит, и прямых a и b.
Докажем, что этот общий перпендикуляр единственный. Допустим, что у прямых a и b есть другой общий перпендикуляр CD. Проведем через точку С прямую b`, параллельную b. Прямая CD перпендикулярна прямой b, а значит, и b`. Так как она перпендикулярна прямой a, то она перпендикулярна плоскости α, а значит, параллельна прямой AB. Выходит, что через прямые AB и CD, как через параллельные, можно провести плоскость. В этой плоскости будут лежать наши скрещивающиеся прямые AC и BD, а это невозможно, что и требовалось доказать.
Билет 16.
|
|
|
Эллипс. Вывод. Каноническое уравнение. Свойства. Эксцентриситет и директриса.
| Эллипс | ||||
Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Обозначим фокусы F1, F2, расстояние между ними – 2с, постоянную из определения – 2а (по условию 2а > 2с, то есть а > с). Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокусы и точка О находилась на середине отрезка F1F2. В такой системе координат F1(-с; о), F2(с; о) (рис. 28).
 Рис. 28
Выведем уравнение эллипса в выбранной системе координат. Для этого рассмотрим произвольную точку эллипса М(х, у).
По определению
Рис. 28
Выведем уравнение эллипса в выбранной системе координат. Для этого рассмотрим произвольную точку эллипса М(х, у).
По определению  Но
Но  следовательно, следовательно,  Преобразуем это уравнение, дважды возводя в квадрат обе части:
Преобразуем это уравнение, дважды возводя в квадрат обе части:

 Обозначим
Обозначим  Разделив обе части на а2в2, получим каноническое уравнение эллипса: Разделив обе части на а2в2, получим каноническое уравнение эллипса:
Уравнение содержит только четные степени х, у, следовательно, кривая симметрична относительно осей координат. В первой координатной четверти уравнение имеет вид
Рис. 29 Оси симметрии эллипса называются осями эллипса, точка их пересечения 0 – центром эллипса. Ось, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с осями называются вершинами эллипса (А1, А2, В1, В2). Отрезки А1А2 и В1В2, а также их длины 2а и 2в называются соответственно большой и малой осями эллипса. Числа а и в называются соответственно большой и малой полуосями эллипса. Отношение половины расстояния между фокусами к большой полуоси Эксцентриситет характеризует форму эллипса: чем меньше эксцентриситет, тем меньше его малая полуось в отличается от большой полуоси а, то есть тем меньше вытянут эллипс вдоль фокальной оси
Пример 14. Эллипс, симметричный относительно осей координат, проходит через точки Решение. Координаты точек М и А должны удовлетворять уравнению (2.22): |
Билет 17.
Гипербола. Вывод. Каноническое уравнение. Свойства. Эксцентриситет и директриса.
Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы F1, F2, расстояние между ними – 2с, постоянную из определения – 2а (по условию 2а < 2с, а < с). Выберем систему координат так же, как при выводе уравнения эллипса (см. рис. 28).
По определению  или или 





 Обозначив
Обозначив  и разделив обе части на а2в2, получим каноническое уравнение гиперболы: и разделив обе части на а2в2, получим каноническое уравнение гиперболы:
Кривая симметрична относительно осей координат, так как уравнение содержит только четные степени х, у. В первой координатной четверти уравнение имеет вид
Рис. 30 Полагая в каноническом уравнении у = 0, найдем точки пересечения гиперболы с осью ОХ: х = ±а. При х = 0 уравнение не имеет решений, то есть с осью ОУ гипербола не пересекается. Точки А1(-а; 0) и А2(а; 0) называются вершинами гиперболы. Фокальная ось (ось, на которой лежат фокусы) называется действительной осью гиперболы, а перпендикулярная ей ось – мнимой осью. Действительной осью называется также отрезок А1А2 и его длина 2а. Отрезок, соединяющий точки В1(0; -в) и В2(0; в), а также его длина 2в называются мнимой осью гиперболы. Числа а и в называются соответственно действительной и мнимой полуосями. Отношение Эксцентриситет характеризует форму гиперболы: чем меньше эксцентриситет, тем меньше отношение полуосей гиперболы, то есть тем сильнее вытянут ее основной прямоугольник относительно фокальной оси
Рассмотрим часть гиперболы, расположенную в первой четверти:
Рис. 31
Очевидно, что при неограниченном возрастании х эта разность стремится к нулю, то есть точки М и N неограниченно сближаются. Из симметрии гиперболы относительно осей координат следует, что этим же свойством обладает прямая На рисунке 32 показано, как с помощью основного прямоугольника гиперболы (это прямоугольник со сторонами длиной 2а и 2в, параллельными осями координат) построить асимптоты гиперболы. Из рисунка видно также взаимное расположение гиперболы и ее асимптот.
Рис. 32 Пример 15. Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен Решение. По условию 2с = 26, | ||||
Билет 18.
Парабола. Вывод. Каноническое уравнение. Свойства. Эксцентриситет и директриса.
| Парабола | ||||||||||
Параболой называется множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Обозначим фокус F, расстояние от фокуса до директрисы р. Выберем декартову прямоугольную систему координат так, чтобы ось ОХ проходила через фокус перпендикулярно директрисе в направлении от директрисы к фокусу и начало координат делило пополам расстояние между фокусом и директрисой (рис. 33). Тогда  а уравнение директрисы а уравнение директрисы 
 Рис. 33
Выведем уравнение параболы в выбранной системе координат. Пусть М(х, у) – произвольная точка параболы, МN – перпендикуляр, опущенный из точки М на директрису.
По определению МN = МF.
Но
Рис. 33
Выведем уравнение параболы в выбранной системе координат. Пусть М(х, у) – произвольная точка параболы, МN – перпендикуляр, опущенный из точки М на директрису.
По определению МN = МF.
Но   Тогда
Тогда  
 или или
– каноническое уравнение параболы.
Уравнение содержит у лишь в четной степени, следовательно, кривая симметрична относительно оси ОХ. При х = 0 у = 0, то есть парабола проходит через начало координат. Из уравнения следует, что х ³ 0 – кривая располагается в правой полуплоскости. При х ® +¥ ôуô ® +¥ (рис. 34). Ось симметрии параболы называется ее фокальной осью, точка 0 – вершиной параболы.
Рис. 34 Замечание. При другом выборе системы координат получаются канонические уравнения другого вида (рис. 35, 36, 37).
Рис. 35
Рис. 36
Рис. 37 |
Билет 19.
Общие уравнения кривой второго порядка. Упрощение уравнения с помощью поворота осей.
Для исследования кривых второго порядка, общее уравнение которых имеет вид
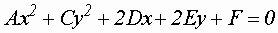 , рассматривается произведение , рассматривается произведение  . .
 .
Выделение полного квадрата
В процессе исследования кривых 2-го порядка, уравнение которых записано в общем виде,
полезна "процедура выделения полного квадрата". Выделяем полный квадрат уравнения .
Выделение полного квадрата
В процессе исследования кривых 2-го порядка, уравнение которых записано в общем виде,
полезна "процедура выделения полного квадрата". Выделяем полный квадрат уравнения
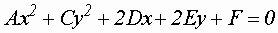 получим: получим:
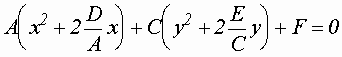 или или
 ,
обозначим: ,
обозначим: 
 ; ; 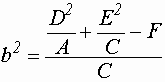 .
П.IV.2(1).
Если .
П.IV.2(1).
Если  , то уравнение задает кривую эллиптического типа. Причем: , то уравнение задает кривую эллиптического типа. Причем:
 , то уравнение задает кривую гиперболического типа. Причем: , то уравнение задает кривую гиперболического типа. Причем:
 .Обозначим: .Обозначим:
 имеем: имеем:  - канонический вид параболы. - канонический вид параболы.
 .Обозначим: .Обозначим:
 - имеем: - имеем:  - канонический вид параболы.
Пример 16. Построить кривую - канонический вид параболы.
Пример 16. Построить кривую 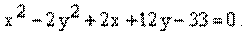 Решение.
Решение.

  Тогда уравнение можно записать в виде
Тогда уравнение можно записать в виде
 или
или  или
или  – уравнение гиперболы с полуосями а = 4,
– уравнение гиперболы с полуосями а = 4,  центр которой находится
в точке О1(-1; 3) (рис. 38). центр которой находится
в точке О1(-1; 3) (рис. 38).
 Рис. 38
Рис. 38
|
Билет 20.
Общее уравнение кривой второго порядка. Упрощение уравнения с помощью переноса начала координат. Центральные кривые.
|
|
|



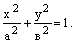
 при возрастании х от 0 до а у убывает от в до 0. Учитывая симметрию, можно сделать вывод о форме эллипса (рис. 29).
при возрастании х от 0 до а у убывает от в до 0. Учитывая симметрию, можно сделать вывод о форме эллипса (рис. 29).
 называется эксцентриситетом эллипса. e < 1.
называется эксцентриситетом эллипса. e < 1.
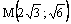 и
и  Написать его уравнение, найти эксцентриситет.
Написать его уравнение, найти эксцентриситет. Решив систему, получим
Решив систему, получим  тогда уравнение эллипса
тогда уравнение эллипса 
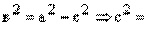


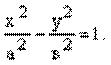
 х ³ а; при возрастании х от а до +¥ у возрастает от 0 до +¥. Учитывая симметрию, можно сделать вывод о форме гиперболы (рис. 30).
х ³ а; при возрастании х от а до +¥ у возрастает от 0 до +¥. Учитывая симметрию, можно сделать вывод о форме гиперболы (рис. 30).
 называется эксцентриситетом гиперболы. e > 1.
называется эксцентриситетом гиперболы. e > 1.
 Покажем, что точки этого графика, расположенные на достаточно большом расстоянии от начала координат, сколь угодно близки к прямой
Покажем, что точки этого графика, расположенные на достаточно большом расстоянии от начала координат, сколь угодно близки к прямой  Пусть М(х, у) и N(х, У) – точки с одной и той же абсциссой, лежащие соответственно на гиперболе и на прямой
Пусть М(х, у) и N(х, У) – точки с одной и той же абсциссой, лежащие соответственно на гиперболе и на прямой  (рис. 31). Рассмотрим разность ординат этих точек:
(рис. 31). Рассмотрим разность ординат этих точек:


 Прямые
Прямые  и
и  называются асимптотами гиперболы.
называются асимптотами гиперболы.

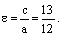 Следовательно, большая полуось гиперболы
Следовательно, большая полуось гиперболы  Тогда малая полуось
Тогда малая полуось  Уравнение гиперболы имеет вид
Уравнение гиперболы имеет вид 





 , то парабола.
, то парабола.  - мнимый эллипс.
- мнимый эллипс.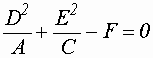 - точка
- точка  .
. , то имеем
, то имеем  - канонический вид
- канонический вид  ,
, имеем:
имеем:  или
или - канонический вид гиперболы.
- канонический вид гиперболы. и учитывая знаки
и учитывая знаки 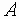 и
и  имеем:
имеем:  - пара пересекающихся прямых.
- пара пересекающихся прямых. , то общее уравнение
, то общее уравнение  задает кривую
задает кривую , то
, то  - кривая параболического типа.
- кривая параболического типа.