 |
Предложение и его функция.
|
|
|
|
Вариант 1
Понятие предельной величины
Под предельной величиной (маржинальной величиной, англ. marginal – находящийся на краю) понимают прирост одной величины, вызванный приростом другой величины на единицу при условии, что все остальные величины остаются неизменными.
В примере с пшеницей прирост минеральных удобрений на единицу (мешок) дает различный прирост урожая. Все приведенные величины прироста урожая (5, 7, 10, 9, 7, 4 ц) и будут предельными величинами, точнее, предельными продуктами такого ресурса, как минеральные удобрения. В соответствии с законом убывающей отдачи величина этого предельного продукта с конкретного момента начинает снижаться. В соответствии с законом возрастающих затрат вначале снижаются, но с определенного момента растут затраты минеральных удобрений (их называют предельными издержками) на прирост каждого центнера пшеницы. Можно сделать вывод, что в этом случае изменяется и доход, получаемый от применения каждого дополнительного мешка удобрений, – его называют предельным доходом.
Предельные величины используются не только производителем, но и потребителем. Например, при оценке им полезности того или иного блага. Потребитель исходит прежде всего из доступности (редкости) для него того или иного блага. Если чистая питьевая вода для него редкость, то за каждый литр ее он готов дорого заплатить (исходя из своей покупательной способности). Но по мере все большей доступности для потребителя питьевой воды он оценивает ее полезность для себя во все меньшую величину и готов платить намного меньше за каждый новый литр. Таким образом, по мере увеличения количества блага его предельная полезность снижается, убывает.
|
|
|
Все это частные случаи теории предельного анализа (предельных величин, маржинального анализа, маржинализма, маржиналистской теории). Она широко используется в экономической теории и практике и базируется на постоянном соотнесении производимых благ (пшеница) или уже имеющихся благ (питьевая вода) с затратами на их производство или их доступностью (редкостью).
Важнейшая идея предельного анализа состоит в том, что на определенном этапе затраты на производство блага начинают расти быстрее, чем само производство этого блага. Другая важнейшая идея предельного анализа такова: чем обильнее благо, тем менее оно ценится.
Общие и средние величины
В маржинальном анализе наряду с предельными величинами используются понятия общей и средней величины.
Общая величина – это суммарный объем произведенной продукции. В примере с пшеницей это 20, 25, 32, 42, 51,58, 62 ц собранного урожая (в зависимости от количества вносимых удобрений).
Средняя величина – это среднее от деления общей величины на количество переменного ресурса.
Среднюю величину можно рассматривать как отдачу от переменного ресурса. В нашем случае это сбор пшеницы в расчете на один мешок удобрений – 20 ц без применения удобрений, 25 ц при применении одного мешка, 16 ц при применении двух мешков, 14 ц – трех мешков, 12,75 ц – четырех мешков и т.д. по убывающей.
Как мы видим, наибольший урожай фермер соберет при внесении 6 мешков удобрений на гектар, наибольший прирост урожая (предельный продукт) даст применение 3 мешков удобрений, но наибольшая отдача – от первого мешка.
Теория предельного анализа имеет важное значение для оптимальной комбинации ресурсов при производстве продукции. В нашем случае, если удобрения дешевы, фермер будет вносить 6 мешков на гектар, если дороги – 3 мешка, если очень дороги – всего 1 мешок, а если мешок удобрений стоит дороже, чем выручка фермера от продажи 5 ц пшеницы, то вообще откажется от применения удобрений. Кстати, в современной России внесение минеральных удобрений в расчете на гектар пашни растет, но оно все еще в два раза ниже, чем в конце 1980-х гг., когда удобрения были дешевы для сельхозпроизводителей. Более подробный анализ оптимальной комбинации ресурсов будет приведен в π. 11.4.
|
|
|
Вариант 2
|
2. Необходимое условие экстремума.
|
|
|
|
|
|
Теорема 1 (необходимые условия экстремума). Если в точке 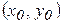 дифференцируемая функция
дифференцируемая функция  имеет экстремум, то её частные производные в этой точке равны нулю:
имеет экстремум, то её частные производные в этой точке равны нулю:  и
и 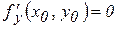 .
.
Зафиксируем одной из переменных. Положим, например, у = у0. Тогда получим функцию  одной переменной, которая имеет экстремум при
одной переменной, которая имеет экстремум при 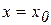 . Следовательно, согласно необходимому условию экстремума функции одной переменной,
. Следовательно, согласно необходимому условию экстремума функции одной переменной, 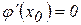 ,
,  .
.
Аналогично можно показать, что 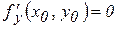 .
.
Геометрически равенства  и
и 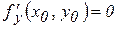 означают, что в точке экстремума функции
означают, что в точке экстремума функции  касательная плоскость к поверхности, изображающей функцию
касательная плоскость к поверхности, изображающей функцию  , параллельна плоскости 0ху, т. к уравнение касательной плоскости есть z = z0.
, параллельна плоскости 0ху, т. к уравнение касательной плоскости есть z = z0.
Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функция  имеет максимум в точке 0(0,0), но не имеет в этой точке частных производных.
имеет максимум в точке 0(0,0), но не имеет в этой точке частных производных.
Точка, в которой частные производные первого порядка функции  равны нулю, т. е.
равны нулю, т. е.  ,
,  , называется стационарной точкой функции.
, называется стационарной точкой функции.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию  . Для неё точка 0(0,0) является критической (в ней
. Для неё точка 0(0,0) является критической (в ней 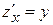 и
и  обращаются в ноль). Однако экстремума в ней функция
обращаются в ноль). Однако экстремума в ней функция  не имеет, т. к. в достаточно малой окрестности точки 0(0,0) найдутся точки, для которых
не имеет, т. к. в достаточно малой окрестности точки 0(0,0) найдутся точки, для которых  (точки I и III четвертей) и
(точки I и III четвертей) и 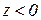 (точки II и IV четвертей).
(точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 2 (достаточное условие экстремума). Пусть в стационарной точке  и некоторой её окрестности функция
и некоторой её окрестности функция  имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке
имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке  значения
значения  ,
,  ,
,  . Обозначим
. Обозначим

Тогда:
1. если  , то функция
, то функция  в точке
в точке  имеет экстремум: максимум, если A < 0, минимум, если A > 0;
имеет экстремум: максимум, если A < 0, минимум, если A > 0;
2. если 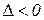 , то функция
, то функция  в точке
в точке  экстремума не имеет.
экстремума не имеет.
В случае  экстремум в точке
экстремум в точке  может быть, может не быть. Необходимы дополнительные исследования. Примем без доказательства.
может быть, может не быть. Необходимы дополнительные исследования. Примем без доказательства.
Пример 1. Найти экстремум функции 
Решение: Здесь 
 Точки, в которых частные производные не существуют, отсутствуют.
Точки, в которых частные производные не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:
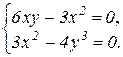
Отсюда получаем точки М1(6;3) и М2(0;0).
Находим частные производные второго порядка данной функции:



В точке М1(6;3) имеем: А = –18, В = 36, С = – 108, отсюда
АС – В2 = -18(-108)-362 = 648,
т. е.  .
. 
В точке М2(0;0) имеем: А = 0, В = 0, С = 0, и, значит,  . Проведем дополнительное исследование. Значение функции z в точке M2 равно нулю:
. Проведем дополнительное исследование. Значение функции z в точке M2 равно нулю:  . Можно заметить, что
. Можно заметить, что 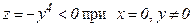 ;
; 
|
|
|
Значит, в окрестности точки М2(0,0) функция z принимает как отрицательные, так и положительные значения. Следовательно, в точке М2 функция экстремума не имеет.
3. Модели функций спроса и предложения.
Спрос и его функция.
Чтобы построить четкую модель рынка, необходимо исследовать в идеальных условиях (при совершенной конкуренции) взаимодействие важнейших категорий рынка - спроса и предложения, за которыми стоят покупатели и продавцы.
Спрос - это количество товаров (услуг), которое покупатели готовы приобрести на рынке.
Величина спроса зависит от ряда факторов. Такую зависимость принято называть функцией спроса:
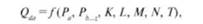
где (2аа - функция спроса на товар; Ра - цена товара; Рь, - цены других товаров, в том числе товаров-заменителей и сопутствующих; К- денежные доходы покупателей; £ - вкусы и предпочтения людей; М - потребительские ожидания; /V- общее число покупателей; Т- накопленное имущество людей.
Основной фактор спроса - цена товара, поэтому зависимость можно упростить:

Функцию спроса можно представить также в виде графика (рис. 10.1).
Соединение между собой точек на графике, каждая из которых является конкретной комбинацией цены и количества, позволяет построить кривую спроса О.
Предложение и его функция.
Предложение - это количество товаров (услуг), которое продавцы готовы продать на рынке. Как и спрос, оно зависит от ряда факторов и может быть формализовано:

где Ом - предложение товара; Ра - цена товара; Рк _ - цены других товаров, в том числе товаров-заменителей и сопутствующих; С - наличие проиводственных ресурсов; К- при-
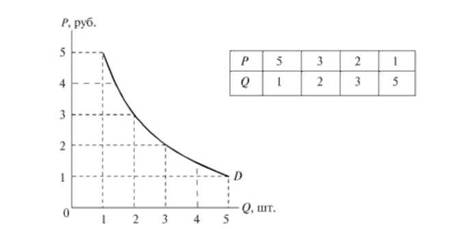
Рис. 10.1. Функция спроса
меняемая технология (время); Я - налоги и дотации у производителей; N - число продавцов.
Основной фактор предложения - тот же, что и спроса, - цена.

Функцию предложения также можно задать с помощью таблицы, которую легко перевести в график (рис. 10.2).
Соединение точек на графике позволяет построить кривую предложения 5, которая имеет восходящий вид.

Рис. 10.2. Функция предложения
4. Стандартная и каноническая формы ЗЛП.
Модель задачи линейного программирования может быть записана в одной из приведенных ниже форм:
1. Общая, или произвольная, форма записи:
max(min)Z= 
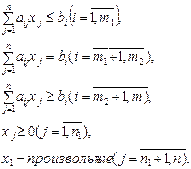
|
при ограничениях:
2 .Симметричная, или стандартная, форма записи:
maxZ=  minZ=
minZ= 





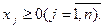
3.Каноническая, или основная, форма записи:
maxZ= 


Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме, т.е. если имеется способ нахождения оптимального решения задачи в одной из указанных форм, то тем самым может быть определен оптимальный план задачи в любой другой форме (говорят о стратегической эквивалентности задачи в любой из форм).
Так, при необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Очевидно, что минимальное значение функции z(x) равно максимальному значению функции- z(x), взятому с противоположным знаком, т.е.
min z(x)=-max(-z(x)).
Неравенство типа > путем умножения левых и правых частей на -1 можно превратить в неравенство типа <, и наоборот. Ограничения-неравенства

преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных xn+i > 0:

В случае необходимости ограничение-равенство

можно записать в виде системы неравенств

Если в ЗЛП какая-то переменная xkне подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных х'k > 0 и х"k > 0:
xk= х'k - х"k.
5. Графический метод решения ЗЛП.
Графический метод решения ЗЛП Нахождение решения ЗЛП на основе ее геометрической интерпретации включает следующие этапы: 1).Строят прямые, уравнения которых получаются в результате замены в ограничениях задачи знаков неравенств на знаки равенств. 2).Находят полуплоскости, определяемые из ограничений задачи. 3).Находят многоугольник решений. 4). Строят вектор. 5). Строят прямую, проходящую через многоугольник решений. 6).Передвигают эту прямую в направлении градиента. 7)Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.
|
|
|



 Средняя величина (AF(x)) определяется как отношение суммарной величины к независимой переменной AF(x)=F(x)/x. Буква А — сокращение от average (средняя).
Средняя величина может обозначаться также
Средняя величина (AF(x)) определяется как отношение суммарной величины к независимой переменной AF(x)=F(x)/x. Буква А — сокращение от average (средняя).
Средняя величина может обозначаться также  = AF(x'). Примеры средних величин в экономике: средне душевой объем потребления, средняя фондоотдача, средняя выручка (доход) AR=R(Q)/Q, средние издержки АС =C(Q)/Q, средний продукт труда AQL =Q(L)/L и т.д.
Средняя величина, как функция независимой переменной, также может задаваться в формульном или графическом виде.
Маржинальная (предельная) величина (MF{x)) определяется как производнаясуммарной величины F(x) по независимой переменной х: MF(x) = F'(x) =
= AF(x'). Примеры средних величин в экономике: средне душевой объем потребления, средняя фондоотдача, средняя выручка (доход) AR=R(Q)/Q, средние издержки АС =C(Q)/Q, средний продукт труда AQL =Q(L)/L и т.д.
Средняя величина, как функция независимой переменной, также может задаваться в формульном или графическом виде.
Маржинальная (предельная) величина (MF{x)) определяется как производнаясуммарной величины F(x) по независимой переменной х: MF(x) = F'(x) = 
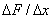 в случае, когда независимая переменная меняется непрерывно. Если суммарная величина меняется дискретно, то под маржинальной (предельной) величиной понимают отношение изменения
в случае, когда независимая переменная меняется непрерывно. Если суммарная величина меняется дискретно, то под маржинальной (предельной) величиной понимают отношение изменения  F(x) суммарной величины F(x) к вызвавшему это изменение изменению (приращению)
F(x) суммарной величины F(x) к вызвавшему это изменение изменению (приращению)  , предельные издержки МС==С'(Q) или
, предельные издержки МС==С'(Q) или  , предельный продукт труда MQL,=Q’(L) или —, предельная полезность MUx=U'(x) или
, предельный продукт труда MQL,=Q’(L) или —, предельная полезность MUx=U'(x) или  и т.д.
Предельная величина, как и все предыдущие, может задаваться формулой или в графическом виде.
Встречаясь с этими величинами в экономике, часто приходится использовать соотношения между ними (например, между суммарными, средними и предельными издержками) и решать задачи на нахождение по одной из этих величин двух других (например, среднего и предельного дохода по суммарному доходу).
Задачи, решаемые экономической наукой и практикой, делятся в зависимости от учета фактора времени на статические и динамические. Статика изучает состояния экономических объектов, относящиеся к определенному моменту или периоду времени, без учета изменения их параметров во времени. В динамических задачах отражается не только зависимость переменных от времени, но и их взаимосвязи во времени. Например, динамика инвестиций определяет динамику величин основного капитала, что в свою очередь является важнейшим фактором изменения объема выпуска.
Время в экономической динамике может рассматриваться как непрерывное или дискретное. Непрерывное время удобно для моделирования, так как позволяет использовать аппарат дифференциального исчисления и дифференциальных уравнений. Дискретное время удобно для приложений, поскольку статистические данные всегда дискретны и относятся к конкретным единицам времени. Для дискретного времени может использоваться аппарат разностных уравнений. Заметим, что большинство известных моделей экономической динамики существуют как в непрерывном, так и в дискретном вариантах. В обоих вариантах для них могут быть получены, как правило, аналогичные результаты, и уровень сложности самих моделей примерно одинаков.1
и т.д.
Предельная величина, как и все предыдущие, может задаваться формулой или в графическом виде.
Встречаясь с этими величинами в экономике, часто приходится использовать соотношения между ними (например, между суммарными, средними и предельными издержками) и решать задачи на нахождение по одной из этих величин двух других (например, среднего и предельного дохода по суммарному доходу).
Задачи, решаемые экономической наукой и практикой, делятся в зависимости от учета фактора времени на статические и динамические. Статика изучает состояния экономических объектов, относящиеся к определенному моменту или периоду времени, без учета изменения их параметров во времени. В динамических задачах отражается не только зависимость переменных от времени, но и их взаимосвязи во времени. Например, динамика инвестиций определяет динамику величин основного капитала, что в свою очередь является важнейшим фактором изменения объема выпуска.
Время в экономической динамике может рассматриваться как непрерывное или дискретное. Непрерывное время удобно для моделирования, так как позволяет использовать аппарат дифференциального исчисления и дифференциальных уравнений. Дискретное время удобно для приложений, поскольку статистические данные всегда дискретны и относятся к конкретным единицам времени. Для дискретного времени может использоваться аппарат разностных уравнений. Заметим, что большинство известных моделей экономической динамики существуют как в непрерывном, так и в дискретном вариантах. В обоих вариантах для них могут быть получены, как правило, аналогичные результаты, и уровень сложности самих моделей примерно одинаков.1