 |
Двойственность в линейном программировании. Связь между двойственными задачами. Основные теоремы двойственности и их экономический смысл.
|
|
|
|
Пусть на предприятии решили рационально использовать отходы основного производства. В плановом периоде появились отходы сырья т видов в объемах bi единиц (i = 1 ,…, m). Из этих отходов можно наладить выпуск п видов неосновной продукции. аij - норма расхода сырья i -го вида на единицу j- ой (j = 1, …, п) продукции, сj - цена реализации единицы j -й продукции. Неизвестные величины: хj - объемы выпуска j- ой продукции, обеспечивающие предприятию максимум выручки.
(1)
Предположим, что на предприятии появилась возможность реал-ции отходов некоторой орг-ции. Надо установить прикидочные оценки (цены) y1,…ym на эти отходы. Оценки должны быть установлены исходя из следующих требований:
1) общую стоимость отходов сырья покупающая организация стремится минимизировать;
2) предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП:
(2):
Переменные y1,…ym называются двойственными оценками. Из (1), (2) можно показать, что если в качестве прямой принять задачу (2) об определении оптимальных оценок на сырье, то двойственной к ней будет задача (1) об определении оптимального плана выпуска продукции. Имея матем. модель одной из задач, можно построить модель двойственной к ней задачи. Задача, двойственная двойственной, совпадает с исходной, поэтому безразлично, какую задачу принять в качестве прямой, а какую – в качестве двойственной. Свойства двойственных задач:
1. Если прямая задача на max, то двойственная к ней – на min, и наоборот.
2. Если в прямой задаче неравенство имеет вид 
, то в двойственной соответственно 
.
|
|
|
3. Число переменных прямой задачи = числу ограничений двойственной, и наоборот..
4. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
5. Коэфф-ты целевой ф-ии прямой задачи явл-ся свободными членами ограничений двойственной задачи, и наоборот.
6. Число ограничений прямой задачи = числу переменных двойственной, а число ограничений двойственной = числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.
Основные теоремы двойственности и их экономическое содержание
Теорема1(основное нер-во двойс-ти) Для любых допустимых планов Х = 
и
Y = 
прямой и двойственной ЗЛП справедливо неравенство F(X) 
Z(Y), т. е.
(3.3)
Доказательство. Учитывая ограничения обеих ЗЛП, получаем
т. е. имеем неравенство (3.3), которое называется основным неравенством теории двойственности.
Экономическое содержание неравенства (3.3) состоит в том, что для любого допустимого плана производства Х и любого допустимого вектора оценок ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов.
Теорема 2. (критерий оптимальности Канторовича). Если для некоторых допустимых планов Х* и Y* пары двойственных задач выполняется равенство z (X*) = f (Y*), то Х* и Y*являются оптимальными планами соответствующих задач.
Доказательство. Согласно основному неравенству двойственности, для любого допустимого плана Х прямой задачи и допустимого плана Y* двойственной справедливо неравенство z (X) f (Y*). Но по условию
z (X*) = f (Y*). Отсюда, в силу транзитивности отношений и =, получим z (X) z (X*). Так как Х - произвольный план, то z (X*) = max Z, т.е. Х* - оптимальный план прямой ЗЛП.
Аналогично доказывается, что план Y* является оптимальным для двойственной задачи.
Экономическое содержание теоремы 3.2 состоит в том, что план производства Х и вектор оценок ресурсов Y являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
|
|
|
Теорема 3 (малая теорема двойственности). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Теорема 4(основная теорема) Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны. Если целевая функция одной из двойственных задач неограниченна на ОДЗ, то другая задача не имеет решения, поскольку ОДЗ 
.
Рассмотрим пару симметричных двойственных задач представленных выше. Введем доп. переменные хn+ 1 ,..., хn+m в прямую задачу и ym+ 1,..., ут+п в двойственную, приводим модели задач к каноническому виду. Теперь м/у переменными двойственных задач можно установить соответствие, сопоставляя свободнвм переменным одной задачи базисные переменные другой, и наоборот:
Экономическое содержание: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых ф-ций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Двойственные оценки обладают тем свойством, что гарантируют рентабельность оптимального плана и позволяют сопоставить и сбалансировать затраты и результаты системы. Т.о., оптимальность плана означает точное воплощение в оценке произведенной по этому плану продукции оценки всех израсходованных ресурсов, т.е. полное отсутствие непроизводительных затрат.
Теорема 5 (о дополняющей нежесткости).Для того чтобы планы х* и у* пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:
, 
.
Экономическое содержание: двойственные оценки могут служить мерой дефицитности ресурса. Если они 
0, то в силу условия дополняющей жесткости разница между расходом ресурса и его запасом должна = 0, т.е. ресурс является дефицитным и расходуется в процессе производства полностью. Если же расход ресурса < используемого запаса, т.е. ресурс недефицитный, то в силу условия дополняющей жесткости, ее двойственная оценка = 0.
|
|
|
Теорема 6 (об оценках).Двойственные оценки показывают приращение ф-ции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее 
. Двойственные оценки характеризуют эластичность оптимального плана по каждому виду ресурсов, =>, перейдя от дифференциалов к конечным приращениям можно получить 
оценку изменения прибыли в зависимости от изменения ресурсов 
, при 
имеем 
.
Экономическое содержание: двойственные оценки ресурсов показывают как изменяется прибыль предприятия при изменении запасов этих видов ресурсов на единицу.
НА 8 ВОПРОС НЕ ОТВЕТИЛА!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
9. Симплекс метод решения ЗЛП (схема).
10. Постановка транспортной задачи. Нахождение опорного решения методом минимальной стоимости.
Транспортная задача. Метод минимальной стоимости
| 22.12.2011, 12:50 |
Метод минимальной стоимости прост и позволяет построить опорное решение, достаточно близкое к оптимальному, так как использует матрицу стоимостей транспортной задачи C=(cij).
Как и метод северо-западного угла, он состоит из ряда однотипных шагов, на каждом из которых заполняется только одна клетка таблицы, соответствующая минимальной стоимости: 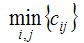 и исключается из рассмотрения только одна строка (поставщик) или один столбец (потребитель). Очередную клетку, соответствующую 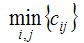, заполняют по тем же правилам, что и в методе северо-западного угла. Поставщик исключается из рассмотрения, если его запасы груза использованы полностью. Потребитель исключается из рассмотрения, если его запросы удовлетворены полностью. На каждом шаге исключается либо один поставщик, либо один потребитель. При этом если поставщик еще не исключен, но его запасы равны нулю, то на том шаге, когда от данного поставщика требуется поставить груз, в соответствующую клетку таблицы заносится базисный нуль и лишь затем поставщик исключается из рассмотрения. Аналогично с потребителем.
Пример 38.2
Используя метод минимальной стоимости построить начальное опорное решение транспортной задачи.
Решение:
1. Запишем отдельно матрицу стоимостей для того, чтобы было удобнее выбирать минимальные стоимости. 
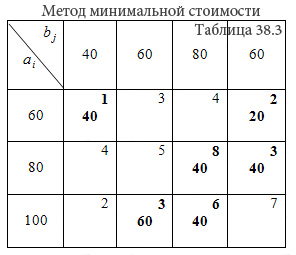2. Среди элементов матрицы стоимостей выбираем наименьшую стоимость C11=1, отмечаем ее кружочком. Данная стоимость имеет место при перевозке груза от 1-го поставщика 1-му потребителю. В соответствующую клетку записываем максимально возможный объем перевозки: x11 = min {a1; b1} = min {60; 40} =40 т.е. минимум между запасами 1-го поставщика и запросами 1-го потребителя.
2.1. Запасы 1-го поставщика уменьшаем на 40. 2.2. Исключаем из рассмотрения 1-го потребителя, так как его запросы полностью удовлетворены. В матрице C вычеркиваем 1-ый столбец.
3. В оставшейся части матрицы C минимальной стоимостью является стоимость C14=2. Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю равна x14 = min {a1'; b4} = min {20; 60} = 20, где a1 со штрихом это оставшиеся запасы первого поставщика. 3.1. Запасы 1-го поставщика исчерпаны, поэтому исключаем его из рассмотрения. 3.2. Запросы 4-го потребителя уменьшаем на 20.
4. В оставшейся части матрицы С минимальная стоимость C24=C32=3. Заполняем одну из двух клеток таблицы (2,4) или (3,2). Пусть в клетку запишем x24 = min {a2; b4} = min {80; 40} =40. 4.1. Запросы 4-го потребителя удовлетворены. Исключаем его из рассмотрения вычеркивая 4-й столбец в матрице C. 4.2. Уменьшаем запасы 2-го поставщика 80-40=40.
5. В оставшейся части матрицы C минимальная стоимость C32=3. Запишем в клетку (3,2) таблицы перевозку x32 = min {a3; b2} = min {100; 60} =60. 5.1. Исключим из рассмотрения 2-го потребителя. Из матрицы C исключаем 2-ой столбец. 5.2. Уменьшим запасы 3-го поставщика 100-60=40
6. В оставшейся части матрицы C минимальная стоимость C33=6. Запишем в клетку (3,3) таблицы перевозку x33 = min {a3'; b3} = min {40; 80} =40 6.1. Исключим из рассмотрения 3-го поставщика, а из матрицы C 3-ю строку. 6.2. Определяем оставшиеся запросы 3-го потребителя 80-40=40.
7. В матрице C остался единственный элемент C23=8. Записываем в клетку таблицы (2,3) перевозку X23=40.
8. Проверяем правильность построения опорного решения. Число занятых клеток таблицы равно N=m+n — 1=3+4 -1. Методом вычеркивания проверяем линейную независимость векторов-условий, соответствующих положительным координатам решения. Порядок вычеркивания показан на матрице X:
Вывод: Решение методом минимальной стоимости (таблица 38.3) является "вычеркиваемым" и, следовательно опорным.
|
|
|
|
| 11. Решение транспортной задачи методом потенциалов (схема решения) | 
| 
| 
|
Пример.
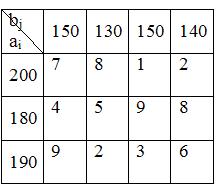1. Проверим, является ли данная задача замкнутой.
Подсчитаем суммарные запасы груза и суммарные потребности заказчиков
 ,  .
Поскольку  , модель транспортной задачи замкнутая, и задача имеет оптимальный план.
2. Построим первый опорный план транспортной задачи методом северо-западного угла.
Начинаем заполнение распределительной таблицы с верхней левой клетки, то есть построение исходного опорного плана начинаем с удовлетворения потребностей первого потребителя b1 за счет запасов первого поставщика a1. Для этого сравниваем запас a1 = 200 с потребностями b1 = 150. Так как a1 > b1, то потребности b1 полностью удовлетворяем за счет a1, и в первую клетку помещаем min (200, 150)=150. У первого поставщика осталось 50 единиц груза. Так как потребности первого получателя груза полностью удовлетворены, исключим из рассмотрения первый столбец, заполнив в нем оставшиеся клетки точками. Далее заполняем таблицу по строкам слева направо и сверху вниз. Следующая самая верхняя левая незаполненная клетка – (1,2). Потребителю b2 поставляем 50 единиц груза, оставшихся у первого поставщика. Поскольку от первого поставщика весь груз вывезен, заполняем оставшиеся клетки первой строки точками. Второму получателю, пока что, недопоставлено 80 единиц груза. Следующая незаполненная клетка – (2,2). Потребителю b2 отправляем недостающие 80 единиц груза, при этом его потребности полностью удовлетворены, поэтому оставшиеся клетки во втором столбце заполняем точками. У второго поставщика a2 осталось еще 100 единиц груза. Аналогичным образом заполняем оставшиеся клетки, пока не удовлетворим всех потребителей и не вывезем все запасы груза у поставщиков.
В результате распределения груза получим первый опорный план, в котором x11 = 150, x12 = 50, x22 = 80, x23 = 100, x33 = 50, x34 = 140. Эти переменные соответствуют заполненным клеткам и являются базисными, остальные переменные, соответствующие клеткам с точками, являются свободными (значения свободных переменных равны нулю). Первый опорный план можно представить в матричном виде
Число заполненных клеток k = 6. Это число должно равняться рангу системы ограничений r = m + n – 1 = 3 + 4 – 1 = 6. Так как k = r = 6, то построенный план является невырожденным. Подсчитаем затраты на перевозку по этому плану
 .
3. Построим первое опорное решение транспортной задачи методом минимальной стоимости (минимального тарифа).
Найдем клетку с минимальным тарифом. Это клетка (1,3) с тарифом
C13 =1. Построение исходного опорного плана начинаем с занесения поставки груза в клетку с наименьшей стоимостью c13. Заполняем клетку x13 = 150. Оставшиеся клетки третьего столбца заполняем точками, так как потребности третьего получателя полностью удовлетворены. У первого поставщика осталось 50 единиц груза. Ищем следующую клетку с минимальным тарифом. Таких клеток две: c14 =2, c32 =2. Заполним сначала клетку (3,2). Поставим в нее x32=min (190, 130)=130. Второй столбец заполняем точками. У третьего поставщика осталось 60 единиц груза. Ищем следующую клетку с наименьшим тарифом – это клетка (1,4). В нее помещаем 50 единиц груза, min(50,140)=50. Первую строку заполняем точками, так как от первого поставщика вывезен весь груз. Четвертому получателю недопоставлено 90 единиц. Аналогичным образом распределяем весь имеющийся груз и получаем первый опорный план перевозок.
Подсчитаем затраты на перевозку по этому плану.
 .
Итак, в каждой строке и в каждом столбце таблицы заполнена хотя бы одна клетка, циклов по заполненным клеткам нет, число заполненных клеток m+n-1=6, следовательно, план опорный и невырожденный.
4. Проверка первого опорного плана (решения) на оптимальность. Метод потенциалов
После построения исходного опорного плана приступаем к проверке его на оптимальность методом потенциалов, который заключается в последовательном улучшении опорных планов транспортной задачи на основе информации, полученной с помощью чисел, называемых потенциалы поставщиков  и потребителей  (, - двойственные переменные, то есть переменные задачи, двойственной к транспортной). Потенциалы находим из условия  , где cij - тарифы заполненных клеток. Будем проверять на оптимальность первый опорный план, построенный методом минимального тарифа. В двойственной задаче одна свободная переменная, поэтому возьмем одну любую из двойственных переменных и приравняем ее к нулю. Возьмем, например,  (выгоднее брать в качестве нулевой переменной ту, которая соответствует строке или столбцу с наибольшим количеством заполненных клеток).
В таблице в дополнительном столбце справа помещаем потенциалы отправителей , а в строке снизу – потенциалы получателей. Составим систему уравнений для определения потенциалов:
Из этой системы находим
Считаем оценки для свободных клеток:
Запишем получившиеся оценки в левом верхнем углу свободных клеток.
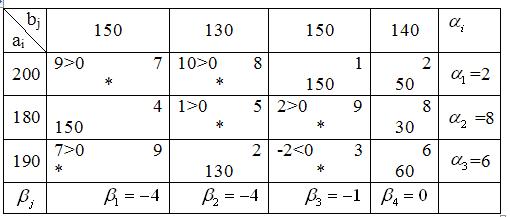Так как среди оценок  имеются отрицательные  , то данный план не является оптимальным. Его можно улучшить перераспределением поставок. Для этого выбираем свободную клетку с наименьшим отрицательным значением  (наибольшим по абсолютной величине). В данном случае это клетка (3,3).
Сроим цикл пересчета, начиная с клетки (3,3), в которую нужно поместить поставку груза (её отмечают знаком «+»), и двигаясь по занятым клеткам (в данном случае это клетки (3,4), (1,4), (1,3)), поочередно отмечая их знаками «-», «+». Если в клетку (3,3) добавили +  , то в смежных по циклу клетках необходимо вычесть для сохранения баланса перевозок по третьей строке и третьему столбцу. Звенья цикла должны быть параллельны строкам или столбцам таблицы, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, а другое – в столбце. Количество вершин в цикле должно быть четно. В результате построения цикла в соответствующих строках и столбцах должно быть парное количество знаков «-», «+».
Определяем величину поставки в клетку (3,3), как минимальную величину из поставок, стоящих в отрицательных клетках, то есть  . Перераспределяем по циклу поставки на величину . Значение записываем в незанятую клетку (3,3), отмеченную знаком «+», двигаясь по циклу, прибавляем эту величину к поставкам в клетках со знаком «+», вычитаем в клетках со знаком «-».
В результате получаем новое опорное решение или новый опорный план, в котором клетки с грузом, равным величине , становятся свободными.
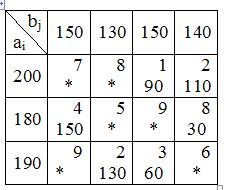Если освобождается больше одной клетки, то есть число заполненных клеток меньше числа m + n - 1, то такой план называется вырожденными, и для определения потенциалов необходимо ввести недостающее количество нулевых элементов в число основных базисных переменных. Свободные клетки заполняют нулевыми поставками так, чтобы они не образовывали цикл по заполненным клеткам, и чтобы в каждой строке и в каждом столбце находилась хотя бы одна заполненная клетка. Проверим новый опорный план на оптимальность. Пусть  =0. Тогда найдем все остальные потенциалы, рассматривая только заполненные клетки и помня, что для них , то есть что сумма потенциалов должна быть равна тарифу, стоящему на пересечении соответствующих потенциалам строки и столбца.
Число заполненных клеток k=m+n-1, следовательно, план невырожденный. Найдем оценки  Для всех клеток с точками, где стоят свободные переменные. Данный опорный план не является оптимальным, так как не все оценки для свободных клеток  , а именно,  .
Возьмем клетку (2,2) за начало цикла пересчета. Цикл будет проходить по клеткам (2,2), (3,2), (3,3), (1,3), (1,4), (2,4) и опять вернется в (2,2).
Ищем количество единиц груза  , перераспределяемых по циклу пересчета, как минимум по клеткам, помеченных знаком минус.  Получаем новый опорный план
Проверяем данный опорный план на оптимальность
Полученный опорный план является оптимальным, так как все оценки для свободных клеток . Выписываем оптимальный план: x11 = 0; x12 = 0; x13 = 60; x14 =140; x21 = 150; x22 = 30; x23 = 0; x24 = 0; x31 = 0; x32 = 100; x33 = 90; x34 = 0. Или в матричной форме
Высчитываем минимальные затраты на транспортировку продукции:
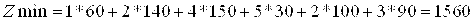12. Постановка транспортной задачи. Нахождение опорного решения методом северо-западного угла.
Сущность метода поясним на примере решения (табл. 8.2.1).
Метод северо-западного угла Таблица 8.2.1
Z1 = 1130
Процесс распределения ресурсов начинается с клетки, расположенной на «северо-западе», то есть в левом верхнем углу. Ей соответствует ресурс а1 = 20 и
потребность b1 = 10. Удовлетворяем потребность полностью, остаётся ресурс, равный 10. Теперь, по правилу, “дораспределяем» остаток ресурса, передав его следующей потребности b2 которая его забирает, но с нехваткой относительно её потребности. Нехватка ресурса для потребности b2 восполняется уже за счёт ресурса a2,расположенного, уже, во второй строчке таблицы. Действия повторяются таким же образом и далее, с образованием ряда ступенек, ведущих в правый нижний угол, где и заканчивается процесс начального распределения.
При нахождении опорного решения данным образом следует иметь в виду, что иногда на некоторой клетке таблицы одновременно заканчиваются и ресурсы, и потребности. Тогда для дальнейшего продвижения (по правилам расчёта) записывается базисный ноль -либо в последующей клетке той же строчки, либо в последующей клеточке того же столбца.
В законченном расчёте любого опорного решения количество заполненных клеток должно быть равно рангу системы минус единица. В противном случае, реализация алгоритма нахождения опорного решения становится невозможной.
Как первое, так и все последующие решения являются возможными для практического осуществления, а эффективность каждого оценивается значением целевой функции.Целевая функция практически служит критерием эффективности того или иного плана, записанного в виде корреспонденций груза в каждой клеточке распределительной таблицы.
13. Решение транспортной задачи сведением ее к стандартной ЗЛП.
Стандартная и каноническая формы задачи линейного программирования
Обратите внимание на то, что в указанных выше двух примерах задачи имели достаточно разный вид: в задаче о диете требовалось найти минимумцелевой функции, а в задаче о плане производства - максимум. В задаче о диете ограничения имели вид
 ,
а в задаче о плане производства - вид
 .
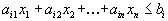Такой разнобой неудобен при разработке алгоритмов решения этих задач. Поэтому имеются некоторые стандартные формы задач линейного программирования, к которым и приводят различные конкретные задачи.
Прежде чем выписывать эти формы, договоримс я об обозначениях. Для более краткой записи мы будем использовать векторную или матричную запись. Подвекторамимы будем понимать вектора-столбцы, например
 ,  ,
Первая стандартная форма задачи линейного программирования имеет вид
Введем вектора
a также вектора
и матрицу
Заметим, что комбинация
Можно использовать и матричные обозначения. Тогда комбинация
Вторая стандартная форма задачи линейного программирования имеет вид
В векторной форме эта задача имеет вид
и в матричной форме -вид
Канонической формой задачи линейного программирования называется задача вида
В векторной форме эта задача имеет вид
и в матричной форме -вид
Во всех этих задачах функцию
Любой набор чисел 14. Нахождение опорного решения транспортной задачи методом минимальной стоимости. Транспортная задача. Метод минимальной стоимости
15. Задача дробно-линейного программирования на примере максимизации рентабельности. Дробно-линейное программирование Дробно-линейное программирование относится к нелинейному программированию, так как имеет целевую функцию, заданную в нелинейном виде. · Решение онлайн · Видеоинструкция Начало формы Целевая функция
Количество предприятий: 2 3 4 5 6 7 8 9 10 Конец формы Рассмотрим задачу дробно-линейного программирования Будем считать, что ПРИМЕР №1. Для производства двух видов изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на каждом из типов оборудования. Известно время обработки каждого из изделий и затраты, связанные с производством одного изделия.
Математическая модель задачи примет вид | |||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
; 
; 
, 
.
есть не что иное, как скалярное произведение векторов 
и 
. Поэтому в векторной форме задача (1.7) примет вид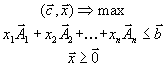
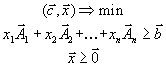
называют вектором коэффициентов линейной формы, вектор 
- вектором ограничений.
, удовлетворяющий ограничениям задачи, называют планом, а множество всех планов - допустимой областью. Тот план, который доставляет экстремум (минимум или максимум) целевой функции, называют оптимальным планом или просто решением задачи линейного программирования.
, 
.
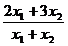