 |
Исследование функции на выпуклость и наличие точек перегиба
|
|
|
|
1. Найти вторую производную 
.
2. Найти точки, в которых вторая производная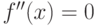 
или не существует.
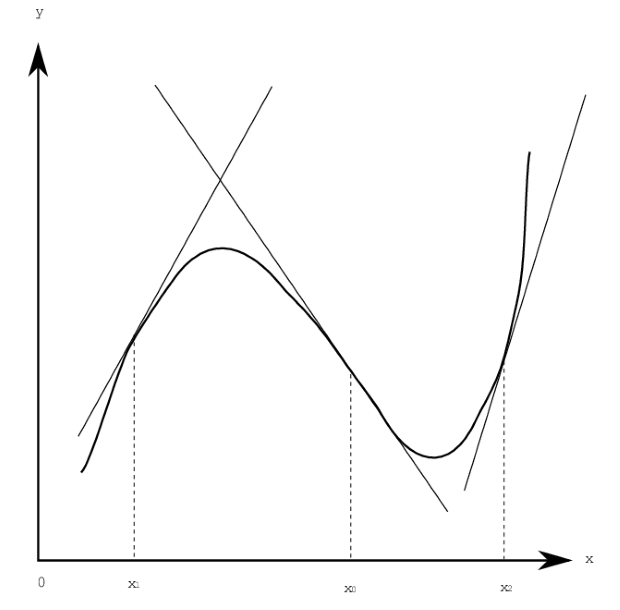
Рис. 3.9. Точки перегиба.
3. Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости или вогнутости и наличии точек перегиба.
Пример. Исследовать функцию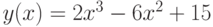 
на выпуклость и наличие точек перегиба.
1. 
.
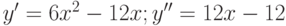2. Вторая производная равна нулю при 
.
3. Вторая производная 
меняет знак при , значит точка — точка перегиба.
На интервале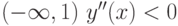 
, значит функция 
выпукла на этом интервале.
На интервале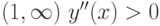 
, значит функция вогнута на этом интервале.
Общая схема исследования функций и построения графика
При исследовании функции и построении ее графика рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность — нечетность. Напомним, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат.
Исследование функции проводится одновременно с построением ее графика.
Пример. Исследовать функцию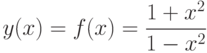 
и построить ее график.
1. Область определения функции —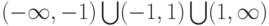 
.
2. Исследуемая функция — четная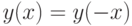 
, поэтому ее график симметричен относительно оси ординат.
3. Знаменатель функции обращается в ноль при 
, поэтому график функции имеет вертикальные асимптоты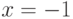 
и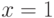 
.
Точки являются точками разрыва второго рода, так как пределы слева и справа в этих точках стремятся к 
.
|
|
|
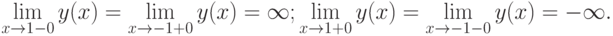
4. Поведение функции в бесконечности.
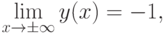
поэтому график функции имеет горизонтальную асимптоту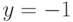 
.
5. Экстремумы и интервалы монотонности. Находим первую производную
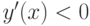при 
, поэтому в этих интервалах функция убывает.
при 
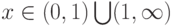, поэтому в этих интервалах функция возрастает.
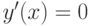при 
, поэтому точка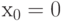 
является критической точкой.
Находим вторую производную
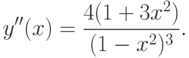
Так как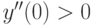 
, то точка 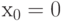является точкой минимума функции .
6. Интервалы выпуклости и точки перегиба.
Функция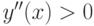 
при 
, значит на этом интервале функция вогнута.
Функция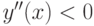 
при 
, значит на этих интервалах функция выпукла.
Функция нигде не обращается в ноль, значит точек перегиба нет.
7. Точки пересечения с осями координат.
Уравнение 
, имеет решение 
, значит точка пересечения графика функции с осью ординат (0, 1).
Уравнение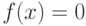 
не имеет решения, значит точек пересечения с осью абсцисс нет.
С учетом проведенного исследования можно строить график функции
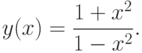
Схематически график функции 
изображен на рис. 3.10.
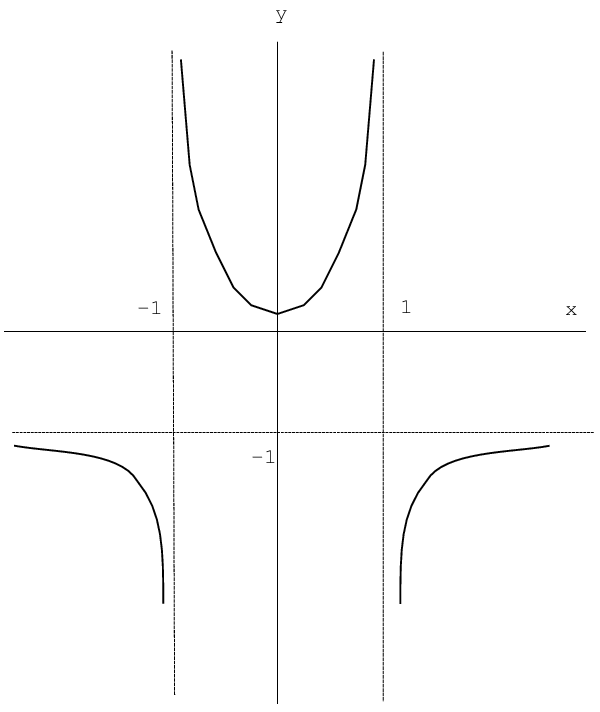
Рис. 3.10. График функции
Асимптоты графика функции
Определение. Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (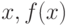
) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.
Асимптоты бывают 3 видов: вертикальные (см. рис. 3.11а), горизонтальные (см. рис. 3.11б) и наклонные (см. рис. 3.11в).
Асимптоты находят, используя следующие теоремы:
Теорема 1. Пусть функция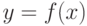 
определена в некоторой окрестности точки 
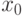(исключая, возможно, саму эту точку) и хотя бы один из пределов функции при 
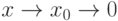(слева) или 
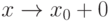(справа) равен бесконечности. Тогда прямая является 
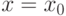вертикальной асимптотой графика функции .
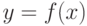Вертикальные асимптоты 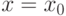следует искать в точках разрыва функции .
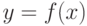Теорема 2. Пусть функция 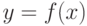определена при достаточно больших 
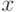и существует конечный предел функции
|
|
|
Тогда прямая 
есть горизонтальная асимптота графика функции .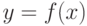
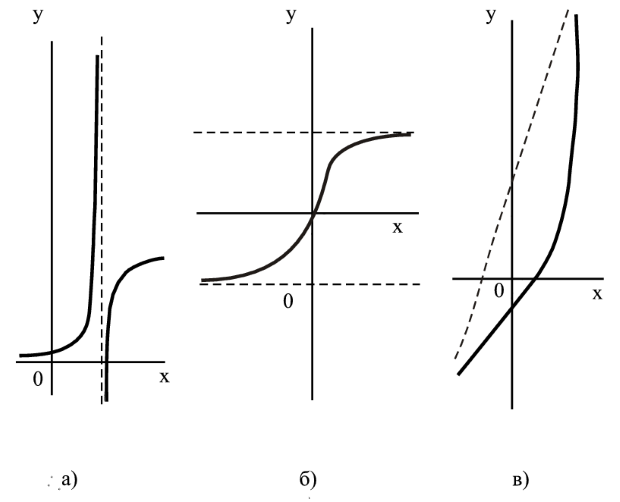
Рис. 3.11. Асимптоты
Теорема 3. Пусть функция 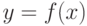определена при достаточно больших 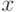и существуют конечные пределы
и
Тогда прямая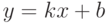 
является наклонной асимптотой графика функции .
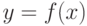Пример. Найти асимптоты графика дробно-рациональной функции
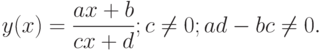
Если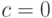 
, то дробно-рациональная функция становится линейной
Особая точка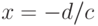 
. Найдём предел 
.
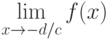Перепишем дробно-рациональную функцию в виде:
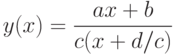
Так как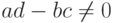 
то при 
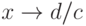числитель дробно-рациональной функции не стремится к нулю. Поэтому прямая — асимптота графика дробно-рациональной функции.
Найдём предел 
.
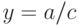— является горизонтальной асимптотой дробно-рациональной функции.
Пример. Найти асимптоты кривой 
.
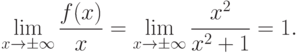
Поэтому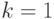 
.
Теперь ищем 
.
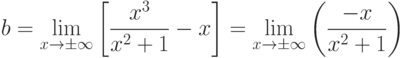
Функция имеет наклонную асимптоту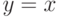 
.
|
|
|
