 |
Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса
|
|
|
|
1. Если функция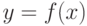 
непрерывна на отрезке 
, то она ограничена на этом отрезке, т.е. существуют такие постоянные и конечные числа 
и 
, что
(см. рис. 3.12а).
2. Если функция 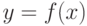непрерывна на отрезке [ 
], то она достигает на этом отрезке наибольшего значения и наименьшего значения m (см. рис. 3.12б).
3. Если функция 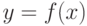непрерывна на отрезке [ ], и значения её на концах отрезка 
и 
имеют противоположные знаки, то внутри отрезка найдётся точка 
, такая, что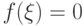 
(см. рис. 3.12в).
Рис. 3.12. Иллюстрации к теоремам Вейерштрасса
17. Условия Куна-Таккера в задаче нелинейного программирования.
Найти векторы 
,удовлетворяющие следующим условиям
(3)
(4)
(5)
(6)
(7)
Прежде всего проиллюстрируем условия Куна — Таккера на примере.
Пример 3
Минимизировать 
при ограничениях 
Решение.
Записав данную задачу в виде задачи нелинейного программирования (0)-(2), получим
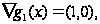
Уравнение (3), входящее в состав условий Куна—Таккера, принимает следующий вид:
откуда
Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде
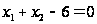
Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид
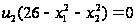
Заметим, что на переменные 
и 
накладывается требование неотрицательности, тогда как ограничение на знак 
отсутствует.
Таким образом, этой задачи условия Куна—Танкера записываются в следующем виде:
18. Пример задач нелинейного программирования и графический метод их решения.
В общем виде задача нелинейного программирования (ЗНП) формулируется следующим образом: найти решение X*= 
системы ограничений
(6) 
при котором целевая функция
(7) 
принимает наибольшее (или наименьшее) значение. Предполагается, что хотя бы одна из функций в (6) или в (7) не линейна.
|
|
|
Для ЗНП в отличие от ЗЛП нет единого метода решения. В зависимости от вида целевой функции (7) и системы ограничений (6) разработаны специальные методы решения, например, метод множителей Лагранжа для ЗНП с системой ограничений, состоящей только из уравнений, и при условии, что все функции в (6) и (7) имеют непрерывные частные производные.
В ЗНП разыскивается наибольшее или наименьшее значение целевой функции – ее глобальный максимум или глобальный минимум. Однако целевая функция может иметь локальные экстремумы, что затрудняет решение ЗНП, так как большинство существующих методов нелинейного программирования не позволяет установить, является ли найденный экстремум локальным или глобальным.
ЗНП с двумя переменными может быть решена графически, как было показано в предыдущих разделах. Графическое решение задачи может быть разбито на следующие части:
1. В прямоугольной системе координат 
определяется область решений системы (6).
2. Определяется тип линий уровня целевой функции 
.
3. Находится линия уровня целевой функции с наибольшим (или наименьшим) значением уровня или устанавливается неразрешимость задачи из-за неограниченности функции на множестве решений системы (6).
4. Определяются координаты точки области решений системы (6), через которую проходит линия уровня, найденная в пункте 3.
Пример. Найти неотрицательное решение системы неравенств
(8) 
при котором функция 
имеет наибольшее значение.
Решение. Область неотрицательных решений системы (8) состоит из двух частей – криволинейных четырехугольников ABCD и EFGH (рис. 1.3), ограниченных осями координат, прямыми 
, 
и 
и гиперболой 
Линиями уровня функции 
=cявляются окружности с центром в начале координатO(0, 0). Окружность наибольшего радиуса, имеющая общие точки с областью решений системы (8), пройдет либо через точкуD, либо через точкуF, так как эти точки наиболее удалены от начала координат. Найдем координаты точекDиF, решая системы
|
|
|
и получим, что D= (2/3, 6) иF= (7, 4/7).
D) = 36 
, 
F) =49 
,
следовательно, max 
F) = 49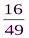 
, 
, 
.
19. Метод множителей Лагранжа нахождения условного экстремума.
Метод Лагранжа ─ это метод решения задачи условной оптимизации, при котором ограничения, записываемые как неявные функции, объединяются с целевой функцией в форме нового уравнения, называемого лагранжианом.
Рассмотрим частный случай общей задачи нелинейного программирования:
Дана система нелинейных уравнений (1):
(1) gi(x1,x2,…,xn)=bi(i=1..m),
Найти наименьшее (или наибольшее) значение функции (2)
(2) f(х1,х2,…,хn),
если отсутствуют условия неотрицательности переменных и f(х1,х2,…,хn) иgi(x1,x2,…,xn) ─ функции, непрерывные вместе со своими частными производными.
Чтобы найти решение этой задачи, можно применить следующий метод: 1. Вводят набор переменных λ1,λ2,…,λm, называемых множителями Лагранжа, составляют функцию Лагранжа (3)
(3) F(х1,х2,…,хn,λ1,λ2,…,λm) =f(х1,х2,…,хn)+ 
λi[bi-gi(x1,x2,…,xn)].
2. Находят частные производные от функции Лагранжа по переменным xiиλiи приравнивают их нулю.
3. Решая систему уравнений, находят точки, в которых целевая функция задачи может иметь экстремум.
4.Среди точек, подозрительных не экстремум, находят такие, в которыхдостигается экстремум, и вычисляют значения функции в этих точках.
4. Сравнить полученные значения функции fи выбрать наилучшее.
Задача:
По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве х1 изделия Iспособом затраты равны 4*х1+х1^2 руб., а при изготовлении х2 изделийIIспособом они составляют 8*х2+х2^2 руб. Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.
Решение: Математическая постановка задачи состоит в определении наименьшего значения функции двух переменных:
f= 4*x1+x1^2 +8*x2 +x2^2, при условииx1 +x2 = 180.
Составим функцию Лагранжа:
F(x1,x2,λ) = 4*x1+x1^2+8*x2+x2^2+λ*(180-x1-x2).
Вычислим ее частные производные по х1,х2, λи приравняем их к 0:
Перенесем в правые части первых двух уравнений λи приравняем их левые части, получим 4 + 2*x1 = 8 + 2*x2, илиx1 −x2 = 2.
|
|
|
Решая последнее уравнение совместно с уравнением x1 +x2 = 180, находимx1 = 91,x2 = 89, то есть получили решение, удовлетворяющее условиям:
x1,x2 ≥ 0.
Найдем значение целевой функции fпри этих значениях переменных:
F(x1,x2) = 17278
Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке (91,89) функция fимеет минимум.
Можно сравнить это значение со значением fв соседних точках:
f(90,90) = 17280 >17278 =f(91,89).
20. Достаточные условия экстремума ФНП (по второму дифференциалу).
|
|
|
