 |
Оценим долю объясненной дисперсии (используем коэффициент детерминации (см. п.2.2.).
|
|
|
|
Выпишем парный коэффициент детерминации (см. подпись при построении тренда):

Изменение У примерно на 74 % определяется вариацией фактора х, на 26 % - влиянием других факторов. То есть изменения величины стоимости жилой площади на 74% обусловлены колебаниями ее размеров, и на 26 % - колебаниями и изменениями других факторов и условий.
5. Оценим качество построенной модели с точки зрения адекватности.
Для этого проверим выполнение следующих требований:
5.1) Уровни ряда остатков имеют случайный характер. Для проверки выполнения данного требования воспользуемся критерием поворотных точек (пиков).
| -3,829 | -3,4095 | -4,145 | -4,629 | -2,797 | -4,7313 | -6,0229 | -5,7565 | -2,4402 | 3,4693 | 2,4879 | 10,3183 | 7,4092 | 13,9416 |
| + | - | + | + | - | - | + | - | + | + | + | + |
Число поворотных точек р = 8
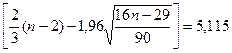
Поскольку р > 5, требование считаем выполненным.
5.2) Математическое ожидание уровня ряда остатков равно нулю.
 =0,029714
=0,029714
Поскольку полученное значение близко к 0, требование считаем выполненным.
5.3) Дисперсия каждого отклонения одинакова для всех х. Для проверки выполнения данного требования используем критерий Гольдфельда-Квандта. Исходные значения х расположим в возрастающем порядке:
| Жилая площадь, х | Цена кв., у. |
| 13,5 | |
| 17,7 | |
| 15,9 | |
| 15,1 | |
| 21,4 | 34,4 |
| 21,1 | |
| 31,1 | |
| 40,5 | |
| 45,9 | 27,2 |
| 46,3 | 28,7 |
| 47,5 | 28,3 |
| 48,7 | |
| 65,8 | |
| 87,2 | 52,3 |
Делим полученную таблицу на 2 равные части
| Жилая площадь, х | Цена кв., у | Жилая площадь, х | Цена кв., у |
| 13,5 | 40,5 | ||
| 17,7 | 45,9 | 27,2 | |
| 15,9 | 46,3 | 28,7 | |
| 15, | 47,5 | 28,3 | |
| 21,4 | 34,4 | 48,7 | |
| 21,1 | 65,8 | ||
| 31,1 | 87,2 | 52,3 |
По каждой группе строим уравнение регрессии:
| Жилая площадь, х | Цена кв., у | 
| 
|
| 13,5 | |||
| 17,7 | 313,29 | 389,4 | |
| 15,9 | |||
| 15,1 | |||
| 21,4 | 34,4 | 457,96 | 736,16 |
| 21,1 | 590,8 | ||
| 31,1 | 967,21 | 870,8 | |
| 154,2 | 3578,46 | 3423,16 |
Чтобы определить параметры линейной модели с помощью метода наименьших квадратов, решим систему уравнений:
|
|
|

Решив полученную систему уравнений при помощи надстройки «Поиск решения» приложения MSExcel, находим:
b0 = 7,01310810173176
b1 = 0,65439846490193
Составим уравнение парной линейной регрессии:

На его основе найдем расчетные значения результативного показателя, а также ряд остатков и остаточные суммы квадратов для первой группы:
| Жилая площадь, х | Цена кв, у | 
| 
| 
| 
| ( )2 )2
|
| 13,5 | 17,477 | -3,977 | 15,816529 | |||
| 17,7 | 313,29 | 389,4 | 18,5888 | 3,4112 | 11,636285 | |
| 15,9 | 20,093 | -4,193 | 17,581249 | |||
| 15,1 | 20,093 | -4,993 | 24,930049 | |||
| 21,4 | 34,4 | 457,96 | 736,16 | 21,0086 | 13,3914 | 179,3296 |
| 21,1 | 590,8 | 25,325 | -4,225 | 17,850625 | ||
| 31,1 | 967,21 | 870,8 | 27,3524 | 0,6476 | 0,4193858 | |
| 154,2 | 3578,46 | 3423,16 | 176,0978 | 0,0622 | 267,5637 |

Рассчитаем аналогичные параметры для второй группы данных:
| Жилая площадь, х | Цена кв, у | 
| 
| 
| 
| ( )2 )2
|
| 40,5 | 1640,25 | 1093,5 | 28,6765 | -1,6765 | 2,81065225 | |
| 45,9 | 27,2 | 2106,81 | 1248,48 | 31,9003 | -4,7003 | 22,0928201 |
| 46,3 | 28,7 | 2143,69 | 1328,81 | 32,1391 | -3,4391 | 11,8274088 |
| 47,5 | 28,3 | 2256,25 | 1344,25 | 32,8555 | -4,5555 | 20,7525803 |
| 48,7 | 2371,69 | 2191,5 | 33,5719 | 11,4281 | 130,60147 | |
| 65,8 | 4329,64 | 3355,8 | 43,7806 | 7,2194 | 52,1197364 | |
| 87,2 | 52,3 | 7603,84 | 4560,56 | 56,5564 | -4,2564 | 18,116941 |
| 381,9 | 259,5 | 22452,17 | 15122,9 | 259,480 | 0,0197 | 258,3216 |
Решив полученную систему уравнений

при помощи надстройки «Поиск решения» приложения MSExcel, находим:
b0 = 4,49765806824428
b1 = 0,59705785159018
Составим уравнение парной линейной регрессии:
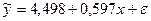

По критерию Гольдфельда-Квандта найдем расчетное значение


(табличные значения критерия Фишера – в Приложении 5).
табличные значения критерия Фишера =FРАСП(0,05;2;2)
Поскольку  <
<  , то условие гомоскедастичности выполнено.
, то условие гомоскедастичности выполнено.
5.4) Значения уровней ряда остатков независимы друг от друга. Проверку на отсутствие автокорреляции осуществим с помощью d-критерия Дарбина-Уотсона:
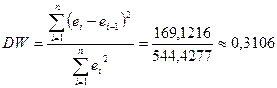
Поскольку d< d1 0,31<1,08 (табличные значения критерия – в Приложении 2), то гипотеза об отсутствии автокорреляции отвергается, и имеется значительная автокорреляция.
|
|
|
5.5) Уровни ряда остатков распределены по нормальному закону. Проверку выполнения требования проведем по RS-критерию:


Для объема генеральной совокупности, равного 14, и уровня вероятности ошибки в 5 %, табличные значения нижней и верхней границ RS-критерия равны соответственно 2,92 и 4,09 (табличные значения критерия – в Приложении 3). Поскольку рассчитанное значение критерия не попадает в интервал табличных значений, гипотеза о нормальном распределении отвергается.
Оценим качество построенной модели с точки зрения точности.
Для этого используем среднюю относительную ошибку аппроксимации:
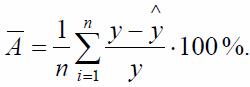
А=-0,7044/14*100%=-5,03%
В среднем смоделированные значения стоимости квартир отклоняются от фактических на 5,03%. Подбор модели к фактическим данным можно оценить как точный, отклонения фактических значений от теоретических не превышает 10–12%.
|
|
|


