 |
Математическая постановка задачи.
|
|
|
|
Переменные:
Х0 - валовой внутренний продукт, млрд. руб.
X] - объем промышленной продукции, млрд. руб.
Х2 - инвестиции в основной капитал, млрд. руб.
Х3 - розничный товарооборот, млрд. руб.
Х4 - объем платных услуг населению, млрд. руб.
Х5 - доходы консолидированного бюджета, млрд. руб.
Хб - расходы консолидированного бюджета, млрд. руб.
Х7 - общая численность официально зарегистрированных безработных, тыс. чел.
Х8 - номинальная начисленная среднемесячная заработная плата, тыс. руб.
Х9 - денежные доходы населения, млрд. руб.
Х10 - денежные расходы и сбережения населения, млрд. руб.
| Вариант | Зависимая переменная | Независимые переменные |
| X0 | X1 – X10 | |
| X1 | X0, X2 - X10 | |
| X2 | X0, X1, X3 - X10 | |
| X3 | X0 - X2, X4 - X10 | |
| X4 | X0 – X3, X5 - X10 | |
| X5 | X0 – X4, X6 - X10 | |
| X6 | X0 – X5, X7 - X10 | |
| X7 | X0 – X6, X8 - X10 | |
| X8 | X0 – X7, X9 - X10 | |
| X9 | X0 – X8, X10 | |
| X10 | X0 – X9 | |
| X0 | X1 – X10 | |
| X1 | X0, X2 - X10 | |
| X2 | X0, X1, X3 - X10 | |
| X3 | X0 - X2, X4 - X10 |
Исходные данные к заданию 2
| X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 |
| 4044,3 | 4356,4 | 605,1 | 1626,7 | 500,2 | 2063,2 | 84,7 | 398,2 | 2612,8 | ||
| 4201,3 | 4376,5 | 620,1 | 1602,5 | 512,7 | 2143,7 | 1869,2 | 84,7 | 400,4 | 2554,4 | 2497,4 |
| 4861,2 | 1880,7 | 2447,7 | 2320,2 | 82,2 | 427,6 | 2783,4 | ||||
| 4906,7 | 862,1 | 1982,7 | 556,1 | 2406,4 | 2496,5 | 80,3 | 440,6 | 2922,6 | 2837,7 | |
| 4886,3 | 4854,9 | 958,4 | 535,4 | 2592,9 | 2277,3 | 77,4 | 449,9 | 2842,8 | 2839,9 | |
| 5788,8 | 4926,3 | 1488,9 | 2193,9 | 582,7 | 2834,4 | 84,4 | 476,4 | 3339,9 | 3274,4 | |
| 5539,7 | 4835,1 | 1231,5 | 2152,1 | 533,1 | 2529,7 | 2563,8 | 73,1 | 487,9 | 3252,5 | 3188,2 |
| 6431,4 | 5254,4 | 1429,6 | 532,9 | 2644,9 | 2434,2 | 497,4 | ||||
| 6681,5 | 5588,4 | 1679,5 | 2344,4 | 550,7 | 2793,7 | 2616,7 | 72,5 | 485,2 | 3503,3 | 3444,4 |
| 5416,7 | 1326,2 | 2341,7 | 567,6 | 2669,2 | 2565,9 | 71,1 | 501,5 | 3309,6 | 3318,1 | |
| 5881,2 | 5477,2 | 1456,8 | 2211,9 | 625,9 | 2904,5 | 69,3 | 503,3 | 3350,4 | 3336,6 | |
| 6355,4 | 5503,9 | 2523,6 | 2629,8 | 716,9 | 2990,5 | 4770,1 | 67,9 | 562,2 | 4172,2 | 4072,7 |
| 4995,9 | 5842,5 | 2017,5 | 633,6 | 2659,8 | 1982,3 | 72,2 | 3299,1 | 3328,2 | ||
| 5175,2 | 5984,6 | 923,8 | 2009,4 | 635,5 | 2636,6 | 2517,9 | 73,4 | 525,4 | 3335,3 | 3292,8 |
| 5971,6 | 6446,3 | 1173,3 | 679,5 | 2943,1 | 3048,8 | 72,8 | 558,5 | 3619,7 | 3608,4 | |
| 5568,1 | 6082,5 | 1156,7 | 2400,1 | 622,6 | 2890,9 | 2984,8 | 71,8 | 561,6 | 3836,6 | 3732,5 |
| 6025,1 | 6301,7 | 1450,2 | 2508,1 | 635,3 | 3051,5 | 2788,9 | 69,3 | 579,3 | 3361,1 | 3376,4 |
| 7025,8 | 6603,9 | 1845,2 | 2684,1 | 680,9 | 66,5 | 4203,3 | ||||
| 6782,7 | 6593,6 | 1566,4 | 2736,6 | 3052,6 | 3026,7 | 62,3 | 612,3 | 3961,9 | 3932,6 | |
| 7775,5 | 7003,6 | 1729,7 | 2824,5 | 678,6 | 3349,7 | 2894,7 | 623,5 | 4016,9 | 3999,9 | |
| 7993,4 | 6823,4 | 1987,3 | 2880,2 | 684,4 | 3456,3 | 3094,8 | 56,4 | 606,4 | 4247,3 | 4192,3 |
| 7169,8 | 6610,8 | 1902,7 | 2812,9 | 788,2 | 3731,2 | 3119,8 | 53,2 | 618,4 | 4146,8 | 4186,5 |
| 7155,5 | 6482,3 | 1839,1 | 2704,2 | 765,1 | 3517,8 | 3327,3 | 52,6 | 611,5 | 4277,5 | 4255,5 |
| 7628,4 | 6491,8 | 3953,7 | 3224,2 | 833,5 | 3823,1 | 6379,6 | ||||
| 6194,3 | 6319,8 | 1351,2 | 2584,7 | 795,3 | 3482,9 | 2321,8 | 53,5 | 617,2 | 4148,2 | 4283,1 |
| 6352,4 | 6607,3 ' | 1185,3 | 2466,7 | 770,1 | 3347,6 | 614,3 | 4180,2 | 4152,6 | ||
| 7220,6 | 7068,7 | 1715,5 | 2928,3 | 815,7 | 3585,4 | 3284,1 | 51,7 | 659,4 | 4601,5 | 4584,6 |
| 6804,6 | 6895,9 | 1536,4 | 3036,4 | 758,7 | 3678,3 | 3856,4 | 50,2 | 661,9 | 4800,2 | 4687,9 |
| 7325,9 | 7459,9 | 1823,1 | 3021,1 | 777,8 | 3801,6 | 3647,7 | 47,7 | 686,9 | 4242,8 | 4284,6 |
| 8336,5 | 7647,9 | 2452,1 | 3237,6 | 837,3 | 4002,1 | 4038,2 | 46,3 | 710,2 | 5270,7 | 5144,8 |
| 8236,2 | 7660,3 | 2076,6 | 3247,1 | 820,4 | 3990,3 | 4067,5 | 46,7 | 4769,1 | ||
| 9214,2 | 8158,4 | 2129,2 | 3436,9 | 829,1 | 3588,1 | 48,6 | 737,3 | 4984,9 | 4984,9 | |
| 9721,8 | 7857,1 | 2502,7 | 3472,8 | 820,8 | 4154,2 | 3781,3 | 46,5 | 713,4 | 5198,5 | |
| 8686,4 | 8336,9 | 2238,7 | 3504,1 | 872,2 | 4322,7 | 4369,4 | 45,5 | 4993,5 | 5050,6 | |
| 8615,6 | 8589,3 | 2417,6 | 3357,1 | 4623,1 | 4506,1 | 45,2 | 736,4 | 5327,6 | 5300,1 | |
| 9378,7 | 8902,3 | 3838,4 | 4034,7 | 974,8 | 4817,9 | 7101,1 | 44,1 | 795,4 | 6410,2 | 6293,5 |
| 7860,4 | 9516,9 | 1468,6 | 3450,4 | 938,5 | 2747,2 | 49,6 | 756,3 | 5272,2 |
|
|
|
Проведение регрессионного анализа средствами MS Excel.
1.5.1. Расчет параметров линейной регрессии с использованием функции ЛИНЕЙН.
Для линейной аппроксимации в Excel существует функция ЛИНЕЙН(изв. зн. Y, изв. зн. X, константа, статистика) она возвращает массив значений описывающих кривую вида:

где изв. зн. Y – это известные значения функции
изв. зн. X – это известные значения аргументов
константа – определяет чему должно равняться b, если константа имеет значение ЛОЖЬ то b полагается равным 1, иначе b вычисляется обычным образом.
|
|
|
статистика – если значение равно ИСТИНА то будет представлена дополнительная регрессионная статистика, если ЛОЖЬ то нет.
Для получения линейной регрессионной зависимости, с выводом всей статистической информации следует выделить диапазон A54:С58, нажать клавишу F2, и ввести формулу =ЛИНЕЙН(P2:P38;N2:O38;1;1),после окончания ввода формулы нажать комбинацию клавиш Ctrl+Shift+Enter так как данная функция возвращает массив значений. В результате в данных ячейках будет полная статистическая информация:
| Линейная зависимость | ||
| 0.645 | 0.176 | 229.123 |
| 0.039 | 0.038 | 94.969 |
| 0.963 | 115.657 | #Н/Д |
| 441.156 | #Н/Д | |
| #Н/Д |
Полученные числа имеют следующий смысл:
| mn | mn-1 | … | b |
| Sen | Sen-1 | … | Seb |
| R2 | Sey | ||
| F | Df | ||
| Ssreg | Ssresid |
Se – стандартная ошибка для коэффициента m
Se b – стандартная ошибка для свободного члена b
R2 – коэффициент детерминированности, который показывает как близко уравнение описывает исходные данные. Чем ближе он к 1, тем больше сходится теоретическая зависимость и экспериментальные данные.
Sey – стандартная ошибка для y
F – критерий Фишера определяет случайная или нет взаимосвязь между зависимой и независимой переменными
Df – степень свободы системы
Ssreg – регрессионная сумма квадратов
Ssresid – остаточная сумма квадратов
Аналогичным образом построим линейную регрессионную зависимость при аргументе Константа равном 0, в диапазоне E54:G58, введя формулу =ЛИНЕЙН(P2:P38;N2:O38;0;1):
| Линейная зависимость | ||
| 0.728 | 0.146 | |
| 0.021 | 0.039 | #Н/Д |
| 0.9980 | 123.365 | #Н/Д |
| 8925.124 | #Н/Д | |
| 2.7E+08 | #Н/Д |
1.5.2. Расчет параметров линейной регрессии с использованием инструмента Регрессия надстройки Пакет анализа.
Для проведения регрессионного анализа выберем пункт меню Сервис/Анализ данных/Регрессия. Откроется следующее диалоговое окно:
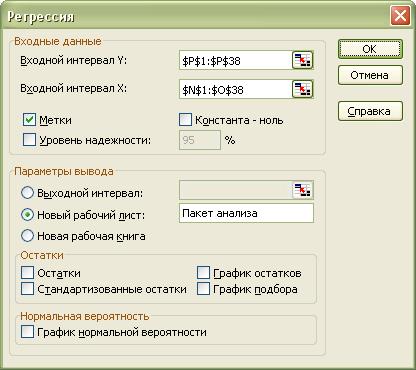
После заполнения полей ввода нажимаем кнопку OK и получаем следующие результаты:
| Регрессионная статистика | |
| Множественный R | 0.981 |
| R-квадрат | 0.963 |
| Нормированный R-квадрат | 0.961 |
| Стандартная ошибка | 115.657 |
| Наблюдения |
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 441.156 | 4.79E-25 | |||
| Остаток | 454805.4 | 13376.63 | |||
| Итого |
|
|
|
| Коэффициенты | Стандартная ошибка | t статистика | P Значение | Нижние 95% | Верхние 95% | Нижние 95.0% | Верхние 95.0% | |
| Y | 229.123 | 94.969 | 2.413 | 0.021 | 36.122 | 422.123 | 36.122 | 422.123 |
| X2 | 0.176 | 0.038 | 4.597 | 0.000 | 0.098 | 0.255 | 0.098 | 0.255 |
| X5 | 0.645 | 0.039 | 16.336 | 1.15E-17 | 0.565 | 0.726 | 0.565 | 0.726 |
Результаты, полученные при расчете с использованием инструмента Регрессия надстройки Пакет анализа, совпали с результатами, полученными при помощи функции ЛИНЕЙН при аргументе Константа имеющем значение ИСТИНА.
|
|
|


