 |
Оценка значимости коэффициентов модели и адекватности модели.
|
|
|
|
Оценка качества модели по критериям Стьюдента и Фишера будет проводиться путём сравнения расчетных значений с табличными.
Для оценки качества модели по критерию Стьюдента фактическое значение этого критерия (tнабл)
сравнивается с критическим значением tкр которое берется из таблицы значений t с учетом заданного уровня значимости (α = 0.05) и числа степеней свободы (n - 2).
Если tнабл > tкр, то полученное значение коэффициента парной корреляции признается значимым.
Критическое значение при 
и 
равно 
.
| Критерий Стьюдента | |||
| Фактор | tнабл | tкр | Значимость |
| Х2 | 7.568 | 2.030 | существенна |
| Х5 | 20.913 | 2.030 | существенна |
Проверим значимость коэффициента детерминации, используя F ‑критерий Фишера.
Вычислим статистику F по формуле:
где:
m = 3 – число параметров в уравнении регрессии;
N = 37 – число наблюдений в выборочной совокупности.
Математической моделью статистического распределения F -статистики является распределение Фишера с 
и 
степенями свободы. Критическое значение этой статистики при 
и 
и 
степенях свободы равно 
.
| Критерий Фишера | ||
| Fрасч | Fкр | Уравнение регрессии |
| 8916.383 | 3.276 | адекватно |
Таким образом, модель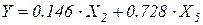 
объясняет 99.8% общей дисперсии признака Y. Это указывает на то, что подобранная модель является адекватной.
Расчет прогнозных значений и суммы квадратов отклонений.
Введем в ячейку Q2 формулу =$F$54*N2+$E$54*O2 (расчет прогнозных значений), затем скопируем ее в ячейки Q3:Q38. В ячейку R2 формулу =(P2-Q2)^2 (расчет суммы квадратов отклонений), затем скопируем ее в ячейки R3:R38, и подсчитаем сумму полученных значений в ячейке R39.
| X2 | X5 | Y | y(x) | (Y - y(x))2 |
| 605.1 | 2063.2 | 1626.7 | 1589.7 | 1367.523 |
| 620.1 | 2143.7 | 1602.5 | 1650.5 | 2303.318 |
| 2447.7 | 1880.7 | 1914.5 | 1144.709 | |
| 862.1 | 2406.4 | 1982.7 | 1876.9 | 11189.53 |
| 958.4 | 2592.9 | 2026.7 | 106.5821 | |
| 1488.9 | 2193.9 | 2180.4 | 182.342 | |
| 1231.5 | 2529.7 | 2152.1 | 2020.4 | 17335.88 |
| 1429.6 | 2644.9 | 2133.1 | 8814.026 | |
| 1679.5 | 2793.7 | 2344.4 | 2277.8 | 4436.216 |
| 1326.2 | 2669.2 | 2341.7 | 2135.8 | 42415.15 |
| 1456.8 | 2211.9 | 2282.7 | 5014.463 | |
| 2523.6 | 2990.5 | 2629.8 | 2543.9 | 7377.384 |
| 2659.8 | 2017.5 | 2059.0 | 1722.637 | |
| 923.8 | 2636.6 | 2009.4 | 2053.4 | 1939.955 |
| 1173.3 | 2943.1 | 2312.8 | 2792.24 | |
| 1156.7 | 2890.9 | 2400.1 | 2272.4 | 16298.85 |
| 1450.2 | 3051.5 | 2508.1 | 2432.0 | 5784.146 |
| 1845.2 | 2684.1 | 2633.3 | 2581.453 | |
| 1566.4 | 3052.6 | 2736.6 | 2449.8 | 82275.65 |
| 1729.7 | 3349.7 | 2824.5 | 2689.8 | 18152.31 |
| 1987.3 | 3456.3 | 2880.2 | 2804.9 | 5676.928 |
| 1902.7 | 3731.2 | 2812.9 | 2992.6 | 32297.9 |
| 1839.1 | 3517.8 | 2704.2 | 2828.0 | 15336.69 |
| 3953.7 | 3823.1 | 3224.2 | 3358.1 | 17922.28 |
| 1351.2 | 3482.9 | 2584.7 | 2731.6 | 21584.07 |
| 1185.3 | 3347.6 | 2466.7 | 2609.0 | 20246.66 |
| 1715.5 | 3585.4 | 2928.3 | 2859.2 | 4768.047 |
| 1536.4 | 3678.3 | 3036.4 | 2900.8 | 18389.81 |
| 1823.1 | 3801.6 | 3021.1 | 3032.3 | 124.6986 |
| 2452.1 | 4002.1 | 3237.6 | 3269.8 | 1034.273 |
| 2076.6 | 3990.3 | 3247.1 | 3206.5 | 1647.633 |
| 2129.2 | 3436.9 | 3375.5 | 3767.099 | |
| 2502.7 | 4154.2 | 3472.8 | 3387.8 | 7220.377 |
| 2238.7 | 4322.7 | 3504.1 | 3472.0 | 1028.291 |
| 2417.6 | 4623.1 | 3357.1 | 3716.7 | 129321.2 |
| 3838.4 | 4817.9 | 4034.7 | 4065.3 | 937.7363 |
| 1468.6 | 3450.4 | 3585.0 | 18128.14 | |
| ∑ | 532666.2 |
|
|
|
Форма отчета
Варианты
| Тарифы на размещение рекламы и характеристики журналов | |||||
| Название журнала | Y, тариф (одна страница цветной рекламы), дол. | X1, планируемая аудитория, тыс. человек | Х2, процент мужчин | Х3, медиана дохода семьи, дол | |
| Audubon | 25 315 | 51,1 | 38 787 | ||
| Better Homes & Gardens | 198 000 | 34 797 | 22,1 | ||
| Business Week | 68,1 | 63 667 | |||
| Cosmopolitan | 15 452 | 17,3 | 44 237 | ||
| Elle | 55 540 | 12,5 | 47 211 | ||
| Entrepreneur | 40 355 | 2 476 | 60,4 | 47 579 | |
| Esquire | 71,3 | 44 715 | |||
| Family Circle | 147 500 | 24 539 | 38 759 | ||
| first For Women | 28 059 | 3 856 | 3,6 | 43 850 | |
| Forbes | 59 340 | 68,8 | 66 606 | ||
| Fortune | 3 891 | 68,8 | 58 402 | ||
| Glamour | 85 080 | 7,8 | |||
| Goff Digest | 6 250 | 78,9 | |||
| Good Housekeeping | 166 080 | 25 306 | 12,6 | 38 335 | |
| Gourmet | 49 640 | 29,6 | 57 060 | ||
| Harper's Bazaar | 52 805 | 2 621 | 11,5 | 44 992 | |
| Inc. | 70 825 | 66,9 | |||
| Kiplinger's Personal Finance | 65,1 | 63 876 | |||
| Ladies' Home Journal | 127 000 | 6,8 | |||
| Life | 63 750 | 14 220 | 46,9 | ||
| Mademoiselle | 55 910 | ||||
| Martha Stewart's Living | 93 328 | 4 849 | 16,6 | ||
| McCalls | 7,6 | 33 823 | |||
| Money | 98 250 | 60,6 | |||
| Motor Trend | 79 800 | 5 281 | 88,5 | 48 739 | |
| National Geographic | 44 326 | ||||
| Natural History | |||||
| Newsweek | 148 800 | 20 720 | 53,5 | 53 025 | |
| Parents Magazine | 72 820 | 18,2 | |||
| PC Computing | 40 675 | 57 916 | |||
| People | 125 000 | 33 668 | |||
| Popular Mechanics | 86,9 | ||||
| Reader's Digest | 42,4 | 38 060 | |||
| Redbook | 95 785 | 13 212 | 8,9 | 41 156 | |
| Rolling Stone | 78 920 | 8 638 | 59,8 | 43 212 | |
| Runner's World | 36 850 | 2 078 | 62,9 | 60 222 | |
| Scientific American | 37 500 | 2 704 | |||
| Seventeen | 71 115 | 5 738 | 37 034 | ||
| Ski | 32 480 | 2 249 | 64,5 | 58 629 | |
| Smart Money | 42 900 | 2 224 | 63,4 | ||
| Smithsonian | 73 075 | 8 253 | 47,9 | ||
| Soap Opera Digest | 35 070 | 7 227 | 10,3 | ||
| Sports Illustrated | 162 000 | 78,8 | 45 897 | ||
| Sunset | 56 000 | 5 276 | 38,7 | 52 524 | |
| Teen | 53 250 | 3 057 | 15,4 | ||
| The New Yorker | 62 435 | 3 223 | 48,9 | ||
| Time | 162 000 | 22 798 | 52,4 | ||
| True Story | 12,2 | ||||
| TV Guide | 42,8 | 37 396 | |||
| U.S. News & World Report | 98 644 | 9 825 | 57,5 | 52 018 | |
| Vanity Fair | 67 890 | 4 307 | 27,7 | ||
| Vogue | 63 900 | 12,9 | 44 242 | ||
| Woman's Day | 137 000 | 22 747 | 6,7 | ||
| Working Woman | 87 500 | 6,3 | 44 674 | ||
| YM | 73 270 | 14,4 | 43 696 | ||
| Среднее значение | 83 534 | 39,7 | 47 710 | ||
| Среднеквадратическое отклонение | 25,9 | 10 225 |
Контрольные вопросы
|
|
|
Парная регрессия
1. Что понимается под парной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие методы применяются для выбора вида модели регрессии?
4. Какие функции чаще всего используются для построения уравнения пар-
5. ной регрессии?
6. Какой вид имеет система нормальных уравнений метода наименьших
7. квадратов в случае линейной регрессии?
8. Как вычисляется и что показывает индекс детерминации?
9. Как проверяется значимость уравнения регрессии?
10. Как проверяется значимость коэффициентов уравнения регрессии?
11. Понятие доверительного интервала для коэффициентов регрессии.
12. Понятие точечного и интервального прогноза по уравнению линейной регрессии.
13. Как вычисляются и что показывают коэффициент эластичности Э, средний коэффициент эластичности Ý?
Множественная регрессия
1. Что понимается под множественной регрессией?
2. Чем отличается модель множественной линейной регрессии от модели парной линейной регрессии? Запишите уравнение множественной линейной регрессии.
|
|
|
3. Какие задачи решаются при построении уравнения регрессии?
4. Какие задачи решаются при спецификации модели?
5. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?
6. Что понимается под коллинеарностью факторов?
7. Как проверяется наличие коллинеарности?
8. Какие подходы применяются для преодоления межфакторной корреляции?
9. Какие функции чаще используются для построения уравнения множественной регрессии?
10. По какой формуле вычисляется индекс множественной корреляции?
11. Как вычисляются индекс множественной детерминации?
12. Что такое коэффициент детерминации? Как с его помощью оценивается адекватность модели?
13. Что означает низкое значение коэффициента множественной корреляции?
14. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
15. Как строятся гипотезы о проверке значимости параметров модели?
16. Как строятся частные уравнения регрессии?
17. Как вычисляются средние частные коэффициенты эластичности?
18. Как строятся доверительные интервалы для параметров модели?
19. Что понимается под гомоскедастичностью ряда остатков?
20. Как проверяется гипотеза о гомоскедастичности ряда остатков?
21. Как называют зависимую переменную в модели?
22. Как называют независимые переменные в модели?
23. Назовите основной метод построения модели.
24. Запишите модель множественной регрессии в общем виде с 3 незав.переменными
25. Запишите сумму квадратов отклонений модели(формула)
26. Что такое RSS?(определение и формула)
27. Как проверить значимость построенной модели в целом?
28. Как проверить значимость коэффициента при переменной X_3?
29. Сфомулируйте экономический смысл коэффициента например при переменно X_5
30. Что такое "короткая модель"множественной регрессии
Литература
1. Шанченко, Н. И.Эконометрика: лабораторный практикум: учебное пособие /Н. И. Шанченко. – Ульяновск: УлГТУ, 2011. – 117 с.
|
|
|
2. Давнис В.В., Тинякова В.И. Компьютерный практикум по эконометрическому моделированию. Воронеж, 2003. - 63 с.
Исходные данные характеризуют цену продажи некоторого товара в отдельные моменты времени. Необходимо построить регрессионную модель динамики изменения данного показателя. Факторы, предположительно оказывающие влияние на данную величину, включают цену продажи товара-субститута, объем продажи товара, объем затрат на рекламу, средние затраты на рекламу.
Цена продажи – зависимая величина, обозначим ее Y.
Факторы, влияющие (предположительно) на величину Y обозначим Xi: X1 – цена товара-субститута, X2 – объем продаж, X3 – объем затрат на рекламу, X4 - средние затраты на рекламу.
Исходные данные
|
|
|
