Расчёт параметров регрессии и корреляции с помощью Excel

Эконометрика

По территориям региона приводятся данные за 200Х г.

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х	Среднедневная заработная плата, руб., у

Задание:

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.

4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

5. Оцените с помощью средней ошибки аппроксимации качество уравнений.

6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.

7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .

8. Оцените полученные результаты, выводы оформите в аналитической записке.

Решение:

Решим данную задачу с помощью Excel.

1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.

Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.

Выделите область ячеек, содержащую данные.

Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.

Рисунок 1 Построение поля корреляции

Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.

2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.

Для этого:

1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;

Рисунок 2 Диалоговое окно «Мастер функций»

5) Заполните аргументы функции:

Известные значения у – диапазон, содержащий данные результативного признака;

Известные значения х – диапазон, содержащий данные факторного признака;

Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;

Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.

Щёлкните по кнопке ОК;

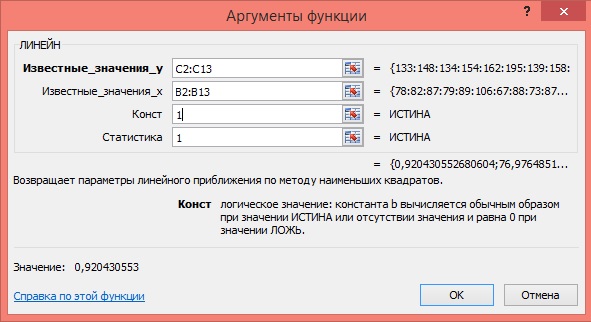
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН

6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Рисунок 4 Результат вычисления функции ЛИНЕЙН

Получили уровнение регрессии:

Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.

3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% - действием других факторов, не включённых в модель.

По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .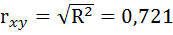

Связь оценивается как тесная.

4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.

Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:

Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.

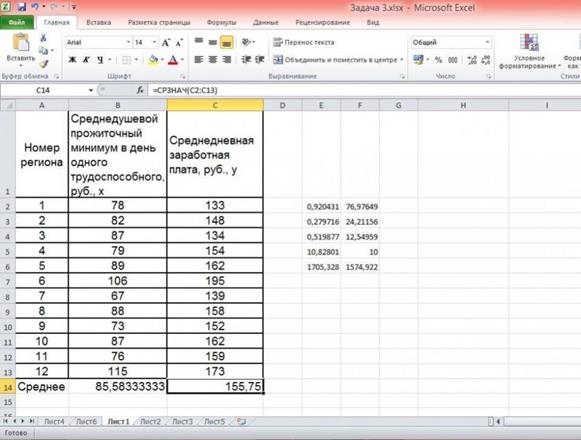
Рисунок 5 Расчёт средних значений функции и аргумент

Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.

С помощью инструмента анализа данных Регрессия можно получить:
- результаты регрессионной статистики,
- результаты дисперсионного анализа,
- результаты доверительных интервалов,
- остатки и графики подбора линии регрессии,
- остатки и нормальную вероятность.

Порядок действий следующий:

1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.

2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.

3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.

• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.

4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.

5) Заполните диалоговое окно ввода данных и параметров вывода:

Входной интервал Y – диапазон, содержащий данные результативного признака;

Входной интервал X – диапазон, содержащий данные факторного признака;

Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;

Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;

6) Новый рабочий лист – можно задать произвольное имя нового листа.

Затем нажмите кнопку ОК.

Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия

Результаты регрессионного анализа для данных задачи представлены на рисунке 7.

Рисунок 7 Результат применения инструмента регрессия

5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.

Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»

Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:

Рисунок 9 Расчёт средней ошибки аппроксимации

Средняя ошибка аппроксимации рассчитывается по формуле:

Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.

6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:

Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).

8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.

Выдвигаем гипотезу Н₀ о статистически незначимом отличии показателей от нуля:

.

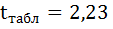для числа степеней свободы

На рисунке 7 имеются фактические значения t-статистики:

t-критерий для коэффициента корреляции можно рассчитать двумя способами:

I способ:

где 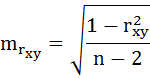– случайная ошибка коэффициента корреляции.

Данные для расчёта возьмём из таблицы на Рисунке 7.

II способ:

Фактические значения t-статистики превосходят табличные значения:

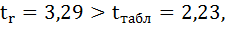
Поэтому гипотеза Н₀ отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.

Доверительный интервал для параметра a определяется как

Для параметра a 95%-ные границы как показано на рисунке 7 составили:

Доверительный интервал для коэффициента регрессии определяется как

Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:

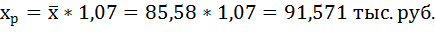
Тогда прогнозное значение прожиточного минимума составит:

Ошибку прогноза рассчитаем по формуле:

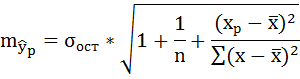
где

Дисперсию посчитаем также с помощью ППП Excel. Для этого:

1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.

2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.

3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.

Рисунок 10 Расчёт дисперсии

Получили значение дисперсии

Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.

Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:

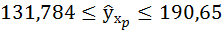
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.

 

Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.

1.5.3. Расчет параметров экспоненциальной регрессии с использованием функции ЛГРФПРИБЛ.

Для экспоненциальной аппроксимации в Excel существует функция ЛГРФПРИБЛ(изв. зн. Y, изв. зн. X, константа, статистика) она возвращает массив значений описывающих кривую вида:

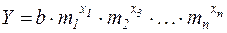
изв. зн. Y – это известные значения функции

изв. зн. X – это известные значения аргументов

константа – определяет чему должно равняться b, если константа имеет значение ЛОЖЬ то b полагается равным 1, иначе b вычисляется обычным образом.

статистика – если значение равно ИСТИНА то будет представлена дополнительная регрессионная статистика, если ЛОЖЬ то нет.

Для получения экспоненциальной регрессионной зависимости, с выводом всей статистической информации следует выделить диапазон I54:K58, нажать клавишу F2, и ввести формулу =ЛГРФПРИБЛ(P2:P38;N2:O38;1;1),после окончания ввода формулы нажать комбинацию клавиш Ctrl+Shift+Enter так как данная функция возвращает массив значений. В результате в данном диапазоне будет получена полная статистическая информация:

Экспоненциальная зависимость
1.0002	1.00007	1030.47
1.9E-05	0.000	0.046
0.940	0.057	#Н/Д
266.115		#Н/Д
1.702	0.109	#Н/Д

 

Полученные числа имеют следующий смысл:

mn	mn-1	…	b
Sen	Sen-1	…	Seb
R2	Sey
F	Df
Ssreg	Ssresid

 

S_e – стандартная ошибка для коэффициента m

S_{e b} – стандартная ошибка для свободного члена b

R² – коэффициент детерминированности, который показывает как близко уравнение описывает исходные данные. Чем ближе он к 1, тем больше сходится теоретическая зависимость и экспериментальные данные.

S_ey – стандартная ошибка для y

F – критерий Фишера определяет случайная или нет взаимосвязь между зависимой и независимой переменными

Df – степень свободы системы

Ssreg – регрессионная сумма квадратов

Ssresid – остаточная сумма квадратов

 

Аналогичным образом построим экспоненциальную регрессионную зависимость при аргументе Константа равном 0, в диапазоне M54:O58, введя формулу =ЛГРФПРИБЛ(P2:P38;N2:O38;0;1):

Экспоненциальная зависимость
1.003	0.99913
0.000244	0.000447	#Н/Д
0.969	1.429	#Н/Д
542.226		#Н/Д
2215.263	71.496	#Н/Д

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: