 |
Системы на растяжение – сжатие
|
|
|
|
Общие указания
Работа состоит из трех задач. В первой задаче необходимо подобрать сечения стержней по заданной внешней нагрузке (или определить грузоподъемность системы). Во второй задаче – определить усилия, напряжения и абсолютные деформации в стержнях, вызванные температурным воздействием; в третьей – определить усилия, напряжения и абсолютные деформации в стержнях, возникающие при монтаже конструкции вследствие неточности их изготовления.
Основные теоретические сведения
Система называется статически неопределимой, если количество неизвестных усилий в ней (опорных реакций, внутренних усилий в стержнях) больше числа независимых уравнений статики, составляемых для рассматриваемой системы.
Таким образом, в статически неопределимой системе невозможно найти все неизвестные, пользуясь только уравнениями равновесия. Разность между количеством неизвестных и числом уравнений статики называется степенью статической неопределимости.
Порядок определения всех неизвестных в статически неопределимых системах (раскрытия статической неопределимости) следующий:
- рассматриваем статическую сторону задачи. Составляем полезное уравнение равновесия (статическое уравнение);
- рассматриваем геометрическую сторону задачи. Составляем уравнение совместности деформаций (геометрическое уравнение). Количество уравнений совместности деформаций равно степени статической неопределимости;
- рассматриваем физическую сторону задачи. Записываем физические уравнения (закон Гука) и выражаем в уравнении совместности деформаций перемещения через усилия;
- составляем систему уравнений (статическое и геометрическое уравнения). Решая полученную систему уравнений, находим все неизвестные усилия.
|
|
|
- производим расчет на прочность по допускаемым напряжениям или допускаемым нагрузкам, или определяем напряжения.
З а д а н и е
Для статически неопределимой стержневой системы (рис. 1.1), состоящей из абсолютно жесткого (недеформируемого) стержня и деформируемых стержней длиной  и
и  , соединенных шарнирами, выполнить следующие расчеты:
, соединенных шарнирами, выполнить следующие расчеты:
- подобрать сечения стержней по заданной внешней нагрузке (или определить грузоподъемность системы);
- определить усилия, напряжения и абсолютные деформации в стержнях, вызванные температурным воздействием;
- определить усилия, напряжения и абсолютные деформации в стержнях, возникающие при монтаже конструкции вследствие неточности их изготовления.
Исходные данные взять из табл. 1.1 и рис. 1.1 в соответствии со своим шифром.
Пример расчета
И с х о д н ы е д а н н ы е:
 м; м;
|  ; ;
| 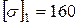 МПа; МПа;
|
 м; м;
| 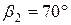 ; ;
|  МПа; МПа;
|
 м; м;
|  МПа; МПа;
|  см; см;
|
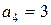 м; м;
|  МПа; МПа;
|  ; ;
|
 м; м;
|  кН; кН;
| 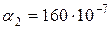 град -1 град -1
|
1. Подбор сечений стержней по заданной внешней нагрузке
(определение грузоподъемности системы)
Р е ш е н и е
1.1. Вычерчиваем в масштабе расчетную схему и проставляем на чертеже все размеры и обозначения (рис. 1.2).
1.2. Убедимся, что рассматриваемая стержневая система является статически неопределимой. Сосчитаем число неизвестных: это продольные силы N1 и N2 в двух деформируемых стержнях и две опорные реакции RA и НА вшарнирно неподвижной опоре А. Таким образом, имеем 4 неизвестные, а число независимых уравнений статики для данной системы равно 3. Система является один раз статически неопределимой.

Рис. 1.1.


Рис. 1.2.
В соответствии с методом сечений рассечем стержни 1 и 2 и, отбросив части стержней, заменим их внутренними усилиями – продольными силами N1 и N2 (рис. 1.3), направления которых определим из следующих соображений: от действия внешней силы Р жесткий стержень наклоняется вниз, при этом первый стержень растягивается и в нем возникает внутреннее усилие N1, а второй стержень сжимается и в нем возникает внутреннее усилие N2.
|
|
|
1.3. Чтобы составить уравнение равновесия, нарисуем план сил (рис. 1.3). Поскольку возникающие в шарнире реакции RA и НА неизвестны, то полезным уравнением равновесия в данном случае является только уравнение суммы моментов относительно шарниров:

 . (1.1)
. (1.1)
1.4. Для составления уравнения совместности деформаций необходимо рассмотреть деформированное состояние системы (рис. 1.4). Под действием внешней силы Р жесткий стержень AD повернется относительно шарнира по часовой стрелке на некоторый малый угол. При этом все точки этого стержня опишут дугу окружности. Поскольку деформации, рассматриваемые в сопротивлении материалов, считаются малыми, заменим эти дуги перпендикулярами. Таким образом, новое положение жесткого стержня AD будет AD2, а точки B и С, как точки жесткого стержня, займут положение B 2 и C2.

Рис. 1.3.

Рис. 1.4.
С другой стороны, точки B и С являются точками стержней, которые деформируются. Первый стержень удлиняется на  (отрезок BB1) и поворачивается (перпендикуляр B1B2), а второй стержень укорачивается на
(отрезок BB1) и поворачивается (перпендикуляр B1B2), а второй стержень укорачивается на  (отрезок СС1) и поворачивается (перпендикуляр С1С2).
(отрезок СС1) и поворачивается (перпендикуляр С1С2).
Геометрическое уравнение, связывающее абсолютные деформации стержней  и
и  , получим из рассмотрения плана перемещений (см. рис. 1.4).
, получим из рассмотрения плана перемещений (см. рис. 1.4).
Из рассмотрения треугольников ABB 2 и ACC2 имеем:
 .
.
Связывая отрезки BB2 и CC2 с деформациями стержней  и
и 
 ;
; 
и учитывая, что AB = a1, AC = a1+a2, получим окончательно уравнение совместности деформаций в виде:
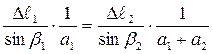 . (1.2)
. (1.2)
1.5. Теперь надо связать деформации стержней с внутренними усилиями. Считая, что материал подчиняется закону Гука (расчет по упругой стадии деформации), запишем физические уравнения:
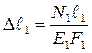 ;
; 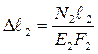 . (1.3)
. (1.3)
Таким образом, решая систему из уравнений (1.1), (1.2), (1.3)можно раскрыть статическую неопределимость системы, т.е. найти внутренние усилия в стержнях N1 и N2.
Дальнейшее решение ведется исходя из условия задачи:
- либо требуется подобрать сечения стержней, если известна внешняя нагрузка и даны допускаемые напряжения материалов стержней;
- либо необходимо определить грузоподъемность системы, если даны площади поперечных сечений стержней.
|
|
|
Подстановкой уравнений (1.3) в уравнение (1.2) получим:
 ;
;
 . (1.4)
. (1.4)
Так как в данном примере:
 МПа
МПа  кН/см2;
кН/см2;  МПа
МПа  кН/см2;
кН/см2;
 ;
;
 м
м  см;
см;  м
м  см;
см; 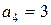 м
м  см;
см;
 м
м  см;
см;
 ;
;  ;
;
 см;
см;  см;
см;
то N1 = 0,732 N2 .
Из уравнения (1.1)имеем:
 ;
;
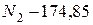 кН;
кН;  кН.
кН.
1.6. Подбор размеров поперечных сечений стержней осуществляем из условия прочности  , которое дает наименьшие значения площадей сечений:
, которое дает наименьшие значения площадей сечений:
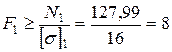 см2;
см2;  см2.
см2.
Учитывая, что в расчетах было заложено соотношение  , окончательно принимаем F 1 = 14,6 см 2, F 2=9,72 см 2.
, окончательно принимаем F 1 = 14,6 см 2, F 2=9,72 см 2.
Следует обратить внимание на то, что первый стержень оказывается недогруженным, так как по условию прочности для него достаточна площадь 8 см2.
1.7. Определение грузоподъемности системы. В данном случае необходимым условием является известная площадь сечений стержней. Дано F 1=5 см 2, F 2=4 см 2. Тогда, решая уравнение (1.1), получим
 ;
;
 .
.
Из уравнения (1.4)имеем:

и окончательно:
 ;
;
 ;
;  .
.
Вычислим в долях от Р напряжения в стержнях
в первом:  кН/см2;
кН/см2;
во втором: 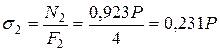 кН/см2.
кН/см2.
Поскольку второй стержень более нагружен ( ), то из условия его прочности имеем:
), то из условия его прочности имеем:

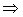
 кН.
кН.
|
|
|


