 |
Определение напряжений, вызванных
|
|
|
|
Температурным воздействием
Рассмотрим случай, когда второй стержень нагревается на  по сравнению с температурой монтажа конструкции (рис. 1.5). Коэффициент линейного расширения материала принять равным
по сравнению с температурой монтажа конструкции (рис. 1.5). Коэффициент линейного расширения материала принять равным 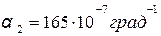 .
.
Знак «минус» в величине 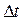 означает, что стержень охлаждается, а знак «плюс» означает, что стержень нагревается.
означает, что стержень охлаждается, а знак «плюс» означает, что стержень нагревается.
Р е ш е н и е
2.1. При нагревании стержень 2 будет расширяться и удлиняться, тем самым жесткий стержень повернется вокруг шарнира А против часовой стрелки и стержень 1 будет сжиматься. Следовательно, в стержне 1 возникает внутреннее усилие N 1, препятствующее его сжатию и направленное к жесткому стержню. С другой стороны, стержень 1 и недеформируемый жесткий стержень препятствуют свободному удлинению стержня 2, поэтому в нем появляются сжимающие напряжения и, как следствие, возникает внутреннее усилие N 2 направленное к жесткому стержню (рис. 1.6).
Составим статическое уравнение
 ;
;  ;
;
 ;
; 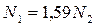 . (1.5)
. (1.5)
2.2.Для составления геометрического уравнения необходимо рассмотреть деформированное состояние системы (рис. 1.7).
При нагреве и удлинении стержня 2 жесткий стержень AВС повернется вверх и займет положение AB2C2. При этом первый стержень укоротится на 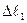 (отрезок BB1) и повернется (перпендикуляр B1B2). Разъединим, мысленностержень 2 в точке С от стержневой системы. Тогда он свободно удлинится при нагреве на величину
(отрезок BB1) и повернется (перпендикуляр B1B2). Разъединим, мысленностержень 2 в точке С от стержневой системы. Тогда он свободно удлинится при нагреве на величину 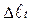 , т.е. точка C переместиться в точку
, т.е. точка C переместиться в точку 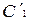 . Чтобы теперь собрать конструкцию, надо этот стержень сжать на
. Чтобы теперь собрать конструкцию, надо этот стержень сжать на  (отрезок
(отрезок 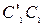 ) и повернуть против часовой стрелки (перпендикуляр
) и повернуть против часовой стрелки (перпендикуляр 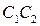 ). Новое положение стержня 2 показано пунктиром.
). Новое положение стержня 2 показано пунктиром.
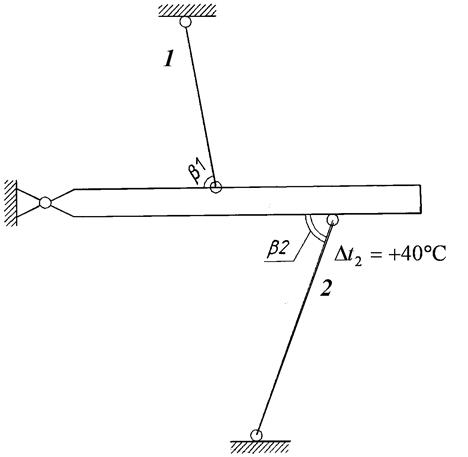
Рис. 1.5.
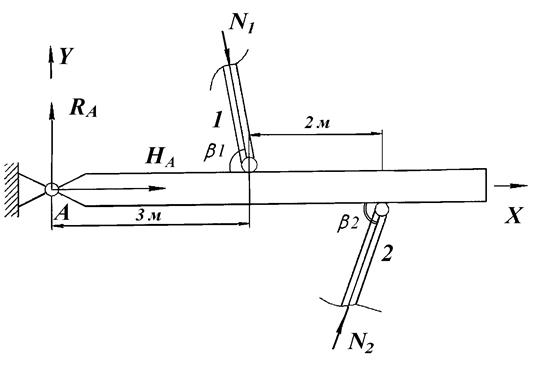
Рис. 1.6.
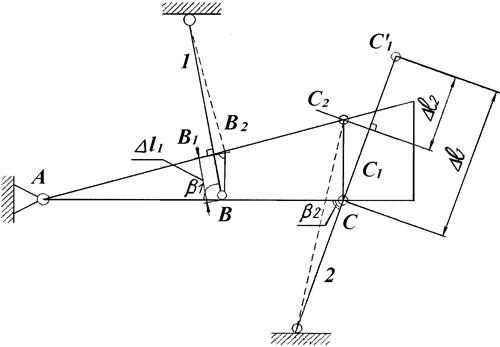
Рис. 1.7.
Аналогично предыдущим задачам из рассмотрения чертежа (рис. 1.7) имеем:
|
|
|
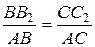 ; ;
| ||
 ; ;
| 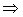 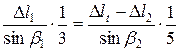 ; ;
| (1.6) |
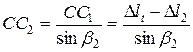 ; ;
| ||
 м; м;  м. м.
|
2.3. Запишем физические уравнения:
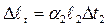 ;
;  ;
;  . (1.7)
. (1.7)
2.4. Подстановкой уравнений (1.7) в уравнение (1.6) получим:
 . (1.8)
. (1.8)
Учитывая уравнение (1.5), перейдем к уравнению относительно неизвестного усилия:
 ;
;
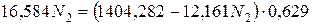 ;
;
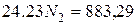 ;
; 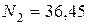 кН;
кН;  кН.
кН.
2.5. Температурные напряжения в стержнях:
в первом: 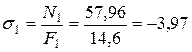 кН/см2
кН/см2 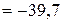 МПа
МПа 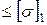 – сжатие;
– сжатие;
во втором:  кН/см2
кН/см2 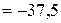 МПа
МПа  – сжатие.
– сжатие.
Напряжениям приписывается отрицательный знак, поскольку в стержнях возникают сжимающие напряжения.
2.6. Удлинения стержней:
 ;
;
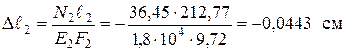 ;
;
 ;
;
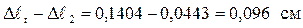 .
.
Определение напряжений, вызванных неточностью
Изготовления стержней
По данным приведенной выше задачи (в предположении, что внешняя сила Р отсутствует) требуется определить усилия, напряжения и абсолютные деформации стержней, возникающие при монтаже вследствие неточности их изготовления. Рассмотрим случай, когда первый стержень изготовлен короче номинального размера на  см (рис. 1.8.).
см (рис. 1.8.).
Знак «минус» при  в условии означает, что стержень изготовлен с зазором, а знак «плюс» означает, что стержень изготовлен длиннее номинального размера.
в условии означает, что стержень изготовлен с зазором, а знак «плюс» означает, что стержень изготовлен длиннее номинального размера.
Р е ш е н и е
3.1. Статическая сторона задачи.
Данная система, также как и в предыдущей задаче, один раз статически неопределима - для плоской системы статика дает три уравнения равновесия, а неизвестных усилий четыре: RA, HA, N1, N2.
При сборке данной системы, поскольку первый стержень изготовлен короче требуемого, его необходимо растянуть, а, следовательно, в нем возникает внутреннее усилие N1 (направлено от жесткого стержня). При этом второй стержень окажется также растянутым и в нем возникает внутреннее усилие N2 (направлено от жесткого стержня, рис. 1.9).
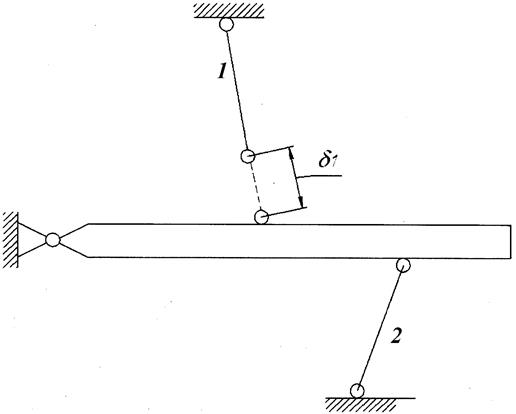
Рис. 1.8.
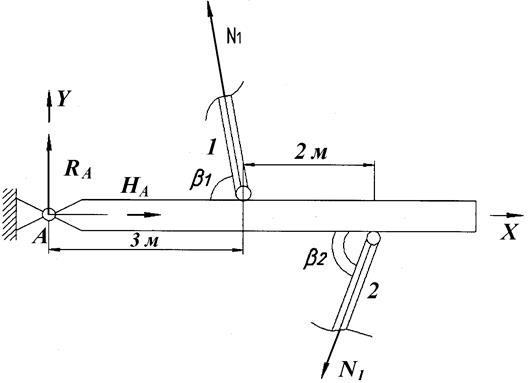
Рис. 1.9.
Уравнение равновесия:
 ;
;  ;
;
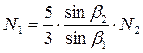 ;
;  . (1.9)
. (1.9)
3.2. Геометрическая сторона задачи (рис. 1.10).
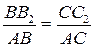 ; ;
| ||
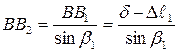 ; ;
| 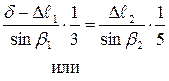
| (1.10) |
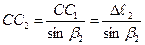
| 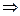 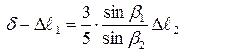
|
Заметим, что при сборке первый стержень фактически необходимо растянуть на 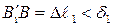 и повернуть (перпендикуляр
и повернуть (перпендикуляр  ). Новое положение первого стержня показано пунктиром. При этом жесткий стержень поворачивается против часовой стрелки, а второй стержень удлиняется на
). Новое положение первого стержня показано пунктиром. При этом жесткий стержень поворачивается против часовой стрелки, а второй стержень удлиняется на 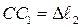 и поворачивается (перпендикуляр
и поворачивается (перпендикуляр 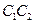 ).
).
|
|
|

Рис. 1.10.
3.3. Физическая сторона задачи (закон Гука)
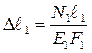 ,
, 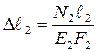 . (1.11)
. (1.11)
3.4. Подстановкой уравнений (1.11) в уравнение (1.10) получим
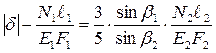 . (1.12)
. (1.12)
Тогда с учетом уравнения (1.9) получим:
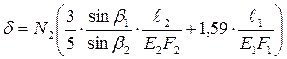 ;
;
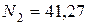 кН;
кН; 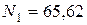 кН.
кН.
3.5. Монтажные напряжения в стержнях
 кН/см2
кН/см2 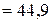 МПа
МПа 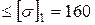 МПа – растяжение;
МПа – растяжение;
 кН/см2
кН/см2 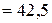 МПа
МПа 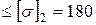 МПа – растяжение;
МПа – растяжение;
Оба полученных напряжения положительны, поскольку стержни растянуты.
3.6. Определим удлинения стержней
 см;
см;
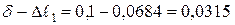 см;
см;
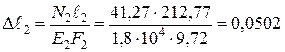 см.
см.
Полученные результаты иллюстрируют малость перемещений по сравнению с габаритными размерами системы и, следовательно, подтверждают допустимость применения указанного выше способа построения плана деформаций.
|
|
|


