 |
Подбор поперечного сечения
|
|
|
|
Подбор поперечного сечения стержня производят по величине осевого момента сопротивления Wz. Осевой момент сопротивления определяем из условия прочности
 ; откуда
; откуда 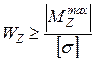 ,
,
где  – допустимое напряжение;
– допустимое напряжение;  – максимальное по абсолютной величине значение изгибающего момента; W z – момент сопротивления сечения.
– максимальное по абсолютной величине значение изгибающего момента; W z – момент сопротивления сечения.
Для прямоугольного сечения момент сопротивления вычисляется из формулы
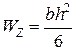 ,
,
где b – ширина сечения; h – высота сечения; (соотношение 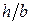 задается).
задается).
Для круглого сечения
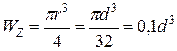 ,
,
где d – диаметр.
Прямоугольное сечение:

| Круглое сечение:

|
По величине момента сопротивления определяется минимально допустимые размеры сечения. После назначения размеров производят проверочный расчет по нормальным и касательным напряжениям. Основой для расчета являются действующие максимальные внутренние усилия  и
и  (см. пример расчета).
(см. пример расчета).
Полная проверка прочности
Пусть в поперечном сечении произвольной балки действуют положительная поперечная сила Q и изгибающий момент М. На рис. 4.4,б и 4.4,в показаны графики  и
и  по высоте массивного сечения, а на рис.4.4,а изображен фасад балки и напряженное состояние в ряде точек по высоте балки. Одна из граней элементарных кубиков совпадает с поперечным сечением. На рис. 4.4,г показано сечение А-А и выделенные в нем элементы. Элементы 1 и 2 выделены у крайних точек сечения. Здесь
по высоте массивного сечения, а на рис.4.4,а изображен фасад балки и напряженное состояние в ряде точек по высоте балки. Одна из граней элементарных кубиков совпадает с поперечным сечением. На рис. 4.4,г показано сечение А-А и выделенные в нем элементы. Элементы 1 и 2 выделены у крайних точек сечения. Здесь  = 0,
= 0,  =
=  или
или 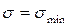 . Элемент 3 выделен у точек нейтрального слоя, где
. Элемент 3 выделен у точек нейтрального слоя, где  = 0,
= 0,  . Элементы 4 и 5 выделены у произвольных точек балки, здесь действуют и
. Элементы 4 и 5 выделены у произвольных точек балки, здесь действуют и  , и
, и  .
.
Таким образом, при поперченном изгибе материал балки находится в неоднородном плоском напряженном состоянии. Условие прочности должно быть записано для опасной точки балки. Опасной будет одна из следующих трех точек:
|
|
|
а) точка, где нормальное напряжение достигает наибольшей величины;
б) точка, где касательное напряжение достигает наибольшей величины;
в) точка, где  и
и 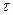 ,хотя и не принимают наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание, т.е. наибольшее расчетное напряжение по принятой теории прочности.
,хотя и не принимают наибольших значений, но в своей комбинации создают наиболее невыгодное сочетание, т.е. наибольшее расчетное напряжение по принятой теории прочности.
| а | б | в | г |

Рис. 4.4.
Необходимо записать три условия прочности. Первая точка расположена в крайних волокнах сечения, где изгибающий момент имеет наибольшее значение (элементы 1 и 2). Напряженное состояние в этой точке линейное и условие прочности запишется в виде
 . (4.1)
. (4.1)
Вторая точка будет находится на нейтральной линии того сечения, где поперечная сила имеет наибольшее значение (элемент 3). В этой точке наблюдается чистый сдвиг и поэтому условие прочности примет вид
 . (4.2)
. (4.2)
Что касается третьей точки, то положение ее не столь определенно. Но где бы она ни была выбрана, в ней будет плоское напряженное состояние (элементы 4 или 5). В нашем случае  и поэтому главные напряжения рассчитываются по формуле:
и поэтому главные напряжения рассчитываются по формуле:
 .
.
Таким образом
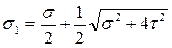 ;
;
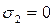 ; (4.3)
; (4.3)
 .
.
Внося эти величины в выражения для расчетных напряжений по третьей (наибольших касательных напряжений) и четвертой (энергетической) теориям прочности, получаем условия прочности
 , (4.4)
, (4.4)
 . (4.5)
. (4.5)
Практика применения и расчета балок показала, что в подавляющем большинстве случаев опасной является крайняя точка того сечения, где  . Подбор сечения балки всегда необходимо производить из условия прочности по нормальным напряжениям (4.1).
. Подбор сечения балки всегда необходимо производить из условия прочности по нормальным напряжениям (4.1).
Проверку прочности по касательным напряжениям по формуле (4.2) необходимо делать только для балок из тонкостенных профилей.
И, наконец, проверку прочности по главным напряжениям по формулам (4.4) или (4.5) необходимо делать только в случае одновременного выполнения следующих условий:
1) балка сделана из тонкостенного профиля с резким переходом от полки к стенке (двутавр, швеллер, коробка);
|
|
|
2) на балке имеется сечение, где Q и М одновременно максимальные или их значения близки к максимуму.
Расчет по всем трем указанным условиям называется полной проверкой прочности.

Рис. 4.5.
З а д а н и е
Для двух балок, показанных на рис. 4.5, построить эпюры поперечных сил и изгибающих моментов и подобрать сечения. Консольная балка (схема I) изготавливается из сосны с допускаемым напряжением  . Для нее необходимо подобрать круглое сечение диаметром D и прямоугольное сечение с отношением сторон
. Для нее необходимо подобрать круглое сечение диаметром D и прямоугольное сечение с отношением сторон 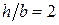 . Балка, изображенная на схеме II, изготавливается из металла. Допускаемые напряжения для двутаврового профиля принять равными
. Балка, изображенная на схеме II, изготавливается из металла. Допускаемые напряжения для двутаврового профиля принять равными  МПа;
МПа;  МПа.
МПа.
В опасном сечении балок, изготовленных из прокатного профиля, построить эпюры распределения нормальных и касательных напряжений по высоте сечения, и сделать полную проверку прочности. Исходные данные для расчета взять в соответствии с шифром из табл. 4.1.
Таблица 4.1
| № строки | Номер схемы | 
| 
| 
| 
| q | Р | М |
| м | кН/м | кН | кНм | |||||
| 1,0 | 2,1 | 1,3 | 1,9 | |||||
| 1,1 | 2,1 | 1,4 | 1,8 | |||||
| 1,2 | 2,0 | 1,5 | 1,7 | |||||
| 1,3 | 1,9 | 1,6 | 1,6 | |||||
| 1,4 | 1,8 | 1,7 | 1,5 | |||||
| 1,5 | 1,7 | 1,8 | 1,4 | |||||
| 1,6 | 1,6 | 1,9 | 1,3 | |||||
| 1,7 | 1,5 | 2,0 | 1,2 | |||||
| 1,8 | 1,4 | 2,1 | 1,1 | |||||
| 1,9 | 1,3 | 2,2 | 1,0 | |||||
| е | в | б | г | д | в | б | e |
Пример расчета
Схема 1. Расчет деревянной балки
Вычерчиваем схему балки в масштабе (рис. 4.6) и проставляем все размеры и заданные силы  МПа.
МПа.
Решение
1. Определяем опорные реакции балок из уравнений статики
 ;
;  ;
;  ;
;
 .
.
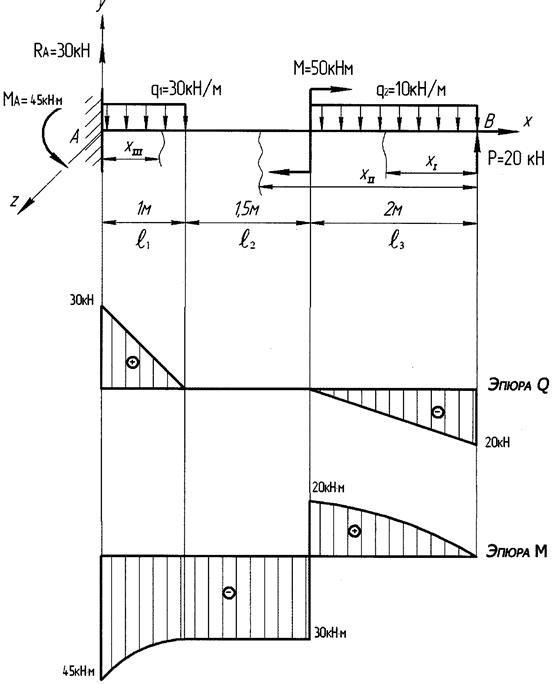
Рис. 4.6.
Уравнение  используем для определения реактивного момента в жёсткой заделке:
используем для определения реактивного момента в жёсткой заделке:
 :
:
 ;
;
 ;
;
 кН.
кН.
Полученное отрицательное значение говорит о том, что первоначальное предположение о направлении реакции оказалось неверным. Для построения эпюр на схеме необходимо показать действительное направление реакции.
2. Составляем аналитические выражения  и Mz на участках и подсчитываем значения на границах участков
и Mz на участках и подсчитываем значения на границах участков
I-й участок 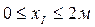
 ;
;  .
.

| ||

| -20 | |

|
II-й участок 2  хII
хII  3,5 м
3,5 м
|
|
|
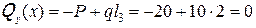 ;
;
 .
.

| 3,5 | |

| ||

| -30 | -30 |
III-й участок 
 ;
;
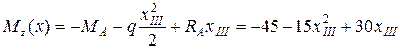 .
.

| ||

| ||

| -45 | -30 |
Строим эпюры  и Mz на рис. 4.6.
и Mz на рис. 4.6.
3. Определяем момент сопротивления из условия прочности
 .
.
4. Подбираем круглое сечение
 ; ;
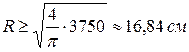 .
Принимаем R = 17 см
(D = 34 см). .
Принимаем R = 17 см
(D = 34 см).
| 
| |
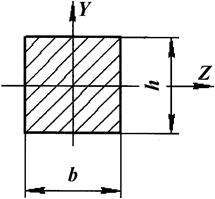
| 5. Подбираем прямоугольное сечение
 ; ; 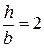 ; ;
 =3750 см3; =3750 см3;
 .
Принимаем b = 18 см;
h = 2b = 36 см. .
Принимаем b = 18 см;
h = 2b = 36 см.
| |
Схема II. Расчет стальной балки двутаврового сечения
Вычерчиваем балку, указывая на схеме все заданные силы и опорные реакции (рис. 4.7),  МПа,
МПа, 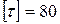 МПа.
МПа.

Рис. 4.7.
Р е ш е н и е
1. Определяем опорные реакции балок. Рекомендуется определить реакции путем составления уравнений равновесия
 ;
;  ,
,
а уравнение  использовать для проверки вычисленных значений реакций.
использовать для проверки вычисленных значений реакций.
 ;
;  ;
;
 кН.
кН.
 ;
; 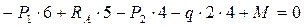 ;
;
 кН.
кН.
Проверка: 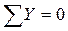 ; - P1+ RA - P2 - q × 4 + RB= 0; -40 + 94 – 30 - 20 × 4 + 56 = 0.
; - P1+ RA - P2 - q × 4 + RB= 0; -40 + 94 – 30 - 20 × 4 + 56 = 0.
Если в результате вычислений реакций одна из них или обе оказываются отрицательными, значит первоначальное предположение об их направлении оказалось неверным. Для построения эпюр на схеме необходимо показать действительное направление реакций.
2. Составляем аналитические выражения 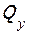 и Mz на всех участках балки и вычисляем значения ординат в характерных сечениях.
и Mz на всех участках балки и вычисляем значения ординат в характерных сечениях.
I-й участок 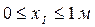
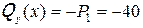 ;
;  .
.

| ||

| -40 | -40 |

| -40 |
II-й участок 
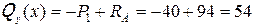 ;
;
 .
.

| ||

| ||

| -40 |
III-й участок 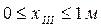
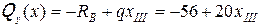 ;
;
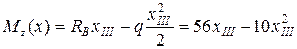 .
.

| ||

| -56 | -36 |

|
IV-й участок 
 ;
;
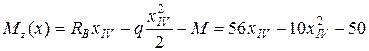 .
.

| ||

| -36 | |

| -4 |
На IV-м участке поперечная сила меняет знак, следовательно, в точке, где 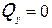 , изгибающий момент имеет экстремальное значение. Установим его, определив сначала координату
, изгибающий момент имеет экстремальное значение. Установим его, определив сначала координату 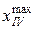 , где
, где 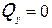 .
.
 ;
; 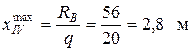
Подставляем теперь полученное значение координаты в выражение для момента на IV- м участке
 .
.
3. Строим эпюры поперечных сил и изгибающих моментов по их вычисленным значениям (рис. 4.7).
4. Определяем требуемый момент сопротивления из условия прочности по наибольшим нормальным напряжениям:
 .
.
Из сортамента выбираем двутавр №24 Wz =289 см 3. Выписываем одновременно все характеристики профиля: h =240 мм; b = 115 мм; d =5,6 мм; t = 9,5 мм; 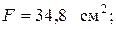 Jz = 3400 см4;
Jz = 3400 см4; 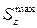 =163 см 3.
=163 см 3.
Наибольшие действующие нормальные напряжения при этом составляют
|
|
|
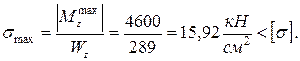
Прочность по нормальным напряжениям обеспечена.
6. Производим проверку прочности по касательным напряжениям. Условие прочности здесь записывается в виде
 ;
;
 кН/см2
кН/см2 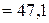 МПа < 90 МПа.
МПа < 90 МПа.
Здесь 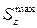 =163 см 3 – статический момент полусечения, берется из сортамента,
=163 см 3 – статический момент полусечения, берется из сортамента,  – ширина сечения в середине высоты профиля.
– ширина сечения в середине высоты профиля.
 7. Производим полную проверку прочности двутавровой балки. Здесь необходимо отметить следующее обстоятельство. Подбор сечения выполняли из условия прочности по нормальным напряжениям, касательные напряжения при этом учтены не были. В то же время могут быть такие случаи нагружения, когда касательные напряжения оказывают существенное влияние на прочность балки. Поэтому и необходима полная проверка прочности.
7. Производим полную проверку прочности двутавровой балки. Здесь необходимо отметить следующее обстоятельство. Подбор сечения выполняли из условия прочности по нормальным напряжениям, касательные напряжения при этом учтены не были. В то же время могут быть такие случаи нагружения, когда касательные напряжения оказывают существенное влияние на прочность балки. Поэтому и необходима полная проверка прочности.
Анализируя эпюры  и Mz, отмечали некоторые опасные сечения, где
и Mz, отмечали некоторые опасные сечения, где  и M одновременно близки к максимальным значениям.
и M одновременно близки к максимальным значениям.
Наиболее опасным по длине балки является сечение, расположенное справа от опоры А, в котором  ; Mz=40 кНм, а также сечение, расположенное справа от места приложения момента, где
; Mz=40 кНм, а также сечение, расположенное справа от места приложения момента, где  ; Mz= 46 кНм. Для примера рассмотрим сечение, находящееся справа от опоры А (
; Mz= 46 кНм. Для примера рассмотрим сечение, находящееся справа от опоры А ( ; Mz= 40 кНм).
; Mz= 40 кНм).
Опасными точками в сечении (рис. 4.8) могут оказаться
1) крайняя точка  ;
;
2) точка 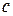 , расположенная в стенке под полкой;
, расположенная в стенке под полкой;
3) точка  на нейтральной оси.
на нейтральной оси.

| Рис. 4.8. |
В точке 
 ;
; 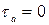 .
.
В точке 
 ;
;  .
.
В точке 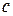 в стенке
в стенке
 ;
;
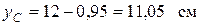 ;
;
 .
.
Площадь полки F1 =11,5 × 0,95=10,925 см 2.
Статический момент полки
 .
.
Расчетные напряжения в точке c по третьей теории прочности
 .
.
По результатам вычислений строим эпюры распределения напряжений по высоте сечения (рис. 4.8 и 4.8).
Аналогично необходимо произвести полную проверку прочности балки в поперечном сечении, где усилия равны  ;
;  – в сечении справа от места приложения внешнего момента М. После этого можно окончательно сделать вывод о прочностной надёжности балки. При выполнении работы следует производить полную проверку балки только в одном опасном сечении. При затруднениях в выборе опасного сечения для расчёта следует обратиться к преподавателю.
– в сечении справа от места приложения внешнего момента М. После этого можно окончательно сделать вывод о прочностной надёжности балки. При выполнении работы следует производить полную проверку балки только в одном опасном сечении. При затруднениях в выборе опасного сечения для расчёта следует обратиться к преподавателю.
___________________
Приложение 1
КОНТРОЛЬНЫЕ вопросы
1. Экспериментальное изучение свойств материалов. Механические характеристики малоуглеродистой стали. Характеристики прочности и пластичности. Наклеп.
2. Испытание материалов на сжатие. Пластическое и хрупкое состояние материала. Закон Гука. Упругие постоянные материала и их определение. Анизотропия материала.
3. Деформация растяжения-сжатия. Продольная сила и ее эпюры (на примере). Вывод формулы для напряжений при растяжении. Условие прочности. Допускаемые напряжения.
4. Вывод формулы для определения перемещения в растянутом стержне. Условие жесткости.
|
|
|
5. Расчет статически неопределимых систем при действии внешних сил.
6. Температурные напряжения в статически неопределимых системах. Влияние высоких температур на механические свойства материала.
7. Монтажные усилия в статически неопределимых системах.
8. Подбор сечений элементов статически неопределимых систем по допускаемым напряжениям.
9. Подбор сечений элементов статически неопределимых систем по допускаемым нагрузкам.
10. Плоское напряженное состояние. Определение нормальных и касательных напряжений на наклонной площадке. Закон парности касательных напряжений.
11. Плоское напряженное состояние. Главные площадки и главные напряжения. Наибольшие касательные напряжения.
12. Определение напряжений на наклонной площадке, если известны главные напряжения. (прямая задача).
13. Определения главных напряжений, если известны напряжения на произвольной площадке.
14. Объемное напряженное состояние. Две формы записи закона Гука.
15. Удельная потенциальная энергия при сложном напряженном состоянии. Энергия изменения объема и энергия изменения формы.
16. Главные напряжения и главные площадки при объемном напряженном состоянии.
17. Наибольшие касательные напряжения при объемном напряженном состоянии.
18. Теория предельных состояний. Причины возникновения теорий прочности. Формулировка теорий прочности.
19. Статические моменты плоской фигуры. Определение положения центра тяжести.
Продолжение прил. 1
20. Понятия о моментах инерции. Моменты инерции для прямоугольника и круга.
21. Преобразование моментов инерции при параллельном переносе осей.
22. Преобразование моментов инерции при повороте осей.
23. Главные оси и главные моменты инерции. Радиус инерции и момент сопротивления.
24. Чистый сдвиг, как частный случай плоского напряженного состояния. Примеры. Закон Гука при чистом сдвиге. Потенциальная энергия сдвига.
25. Расчет заклепочных, болтовых и сварных соединений.
26. Вывод формулы для касательного напряжения при кручении круглого вала.
27. Условие прочности при кручении и подбор по нему сечений сплошного и полого вала.
28. Вывод формулы для угла закручивания вала. Условие жесткости и подбор по нему сечений сплошных и полых валов.
29. Главные напряжения при кручении. Характер разрушения валов.
30. Расчет валов по предельному состоянию. Потенциальная энергия деформации кручения.
31. Кручение стержней прямоугольного сечения. Определения напряжений и угла закручивания.
32. Вывод формул для напряжений в пружине и ее осадки.
33. Вывод дифференциальных зависимостей между изгибающим моментом, поперечной силой и интенсивностью нагрузки при изгибе балки.
34. Вывод формулы для нормальных напряжений при чистом изгибе. Условие прочности, подбор сечения.
35. Вывод формулы для касательных напряжений при изгибе.
36. Главные напряжения при изгибе. Полная проверка прочности балок при изгибе. Центр изгиба. Рациональные сечения балок при изгибе.
Приложение 2
Сортамент прокатной стали
Двутавры стальные горячекатаные (по ГОСТ 8239–89)
 – высота двутавра; – высота двутавра;
 – ширина полки; – ширина полки;
 – толщина стенки; – толщина стенки;
 – средняя толщина полки; – средняя толщина полки;
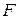 – площадь поперечного сечения; – площадь поперечного сечения;
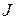 – момент инерции; – момент инерции;
 – момент сопротивления; – момент сопротивления;
 – статический момент полусечения; – статический момент полусечения;
 – радиус инерции. – радиус инерции.
| 
|
| № двутавра | Масса, м·кг | Размеры, мм | 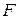 ,
см2 ,
см2
| 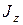 ,
см4 ,
см4
|  ,
см3 ,
см3
|  ,
см ,
см
|  ,
см3 ,
см3
|  ,
см4 ,
см4
|  ,
см3 ,
см3
|  ,
см ,
см
| |||
| h | b | 
| t | ||||||||||
| 9,46 | 4,5 | 7,2 | 39,7 | 4,06 | 17,9 | 6,49 | 1,22 | ||||||
| 11,5 | 4,8 | 7,3 | 14,7 | 58,4 | 4,88 | 33,7 | 27,9 | 8,72 | 1,38 | ||||
| 13,7 | 4,9 | 7,5, | 17,4 | 81,7 | 5,73 | 46,8 | 41,9 | -11,5 | 1,55 | ||||
| 15,9 | 7,8 | 20,2 | 6,57 | 62,3 | 58,6 | 14,5 | 1,7 | ||||||
| 18,4 | 5,1 | 8,1 | 23,4 | 7,42 | 81,4 | 82,6 | 18,4 | 1,88 | |||||
| 5,2. | 8,4 | 26,8 | 8,28 | 23,1 | 2,07 | ||||||||
| 5,4 | 8,7 | 30,6 | 9,13 | 28,6 | 2,27 | ||||||||
| 27,3 | 5,6 | 9,5 | 34,8 | 9,97 | 34,5 | 2,37 | |||||||
| 31,5 | 270. | 6' | 9,8 | 40,2 | 11,2 | 41,5 | 2,54 | ||||||
| 36,5 | 6,5 | 10,2 | 46,5 | 12,3 | 49,9 | 2,69 | |||||||
| 42,2 | 11.2 | 53,8 | 13,5 | 59,9 | 2,79 | ||||||||
| 48,6 | 7,5 | 12,3 | 61,9 | 14,7 | 71,1 | 2 89 | |||||||
| 8,3 | 72,6 | 16,2 | 86,1 | 3,03 | |||||||||
| 66,5 | 14,2 | 84,7 | 18,1 | 3,09 | |||||||||
| 78,5 | 15,2 | 19,9 | 3,23 | ||||||||||
| 92,6 | 16,5 | 21,8 | 3,39 | ||||||||||
| 17,8 | 23,6 | 3,54 |
Продолжение прил. 2
Швеллеры стальные горячекатаные по ГОСТ 8240–89

|  – высота швеллера; – высота швеллера;
 – ширина полки; – ширина полки;
 – толщина стенки; – толщина стенки;
 – средняя толщина полки; – средняя толщина полки;
 – площадь поперечного сечения; – площадь поперечного сечения;
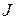 – момент инерции; – момент инерции;
 – момент сопротивления; – момент сопротивления;
 – статический момент полусечения; – статический момент полусечения;
 – радиус инерции; – радиус инерции;
 – расстояние от оси – расстояние от оси  до наружной грани стенки. до наружной грани стенки.
|
| № швеллера | Масса, м·кг | Размеры, мм | 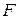 ,
см2 ,
см2
| 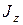 ,
см4 ,
см4
|  ,
см3 ,
см3
|  ,
см ,
см
|  ,
см ,
см
|  ,
см4 ,
см4
| 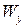 ,
см3 ,
см3
| 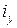 ,
см ,
см
|  ,
см ,
см
| ||||
| h | b | 
| t | ||||||||||||
| 4,84 | 4,4 | 6,16 | 22,8 | 9,1 | 1,92 | 5,59 | 5,61 | 2,75 | 0,95 | 1,16 | |||||
| 6,5 | 5,9 | 4,4 | 7,2 | 7,51 | 48,6 | 2,54 | 8,7 | 3,68 | 1,08 | 1,24 | |||||
| 7,05 | 4,5 | 7,4 | 8,98 | 89,4 | 22,4 | 3,16 | 13,3 | 12,8 | 4,75 | 1,19 | 1,31 | ||||
| 8,59 | 4,5 | 7,6 | 10,9 | Л 74 | 34,8 | 3,99 | 20,4 | 20,4 | 6,46 | 1,37 | 1,44 | ||||
| 10,4 | 4,8 | 7,8 | 13,3 | 50,6 | 4,78 | 29,6 | 31,2 | 8,52 | 1,53 | 1,54 | |||||
| 12,3 | 4,9 | 8,1 | 15,6 | 70,2 | 5,6 | 40,8 | 45,4 | 1,7 | 1,67 | ||||||
| 14,2 | 8,4 | 18,1 | 93,4 | 6,42 | 54,1 | 63,3 | 13,8 | 1,87 | 1,8 | ||||||
| 1ба | 15,3 | 19,5 | 6,49 | 59,4 | 78,8 | 16,4 | 2,01 | ||||||||
| 16,3 | 5,1 | 8,7 | 20,7 | 7,24 | 69,8 | 2,04 | 1,94 | ||||||||
| 18а | 17,4 | 5,1 | 9,3 | 22,2 | 7,32 | 76,1 | 2,18 | 2,13 | |||||||
| 18,4 | 5,2 | 23,4 | 8,07 | 87,8 | 20,5 | 2,2 | 2,07 | ||||||||
| 5,4 | 9,5 | 26,7 | 8,89 | ПО | 25,1 | 2,37 | 2,21 | ||||||||
| 5,6 | 30,6 | 9,73 | 31,6 | 2,6 | 2,42 | ||||||||||
| 27,7 | 10,5 | 35,2 | 10,9 | 37,3 | 2,73 | 2,47 | |||||||||
| 31,8 | 6,5 | 40,5 | 43,6 | 2,84 | 2,52 | ||||||||||
| 36,5 | 11,7 | 46,5 | 13,1 | 51,8 | 2,97 | 2,59 | |||||||||
| 41,9 | 7,5 | 12,6 | 53,4 | 14,2 | 61,7 | 3,1 | 2,68 | ||||||||
| 48,3 | 13,5 | 61,5 | 15,7 | 73,4 | 3,23 | 2,75 | |||||||||
Продолжение прил. 2
Уголки стальные горячекатаные равнополочные (по ГОСТ 8509–86)
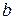 – ширина полки; – ширина полки;
 –толщина полки; –толщина полки;
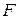 – площадь поперечного сечения; – площадь поперечного сечения;
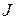 – момент инерции; – момент инерции;
 – радиус инерции; – радиус инерции;
 – центробежный момент инерции; – центробежный момент инерции;
 – расстояние до центра тяжести. – расстояние до центра тяжести.
| 
|
| № уголка | Масса 1 м уголка, кг | Размеры, мм | 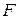 , см2 , см2
|  ,
см4 ,
см4
|  ,
см ,
см
| 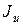 ,
max,
см4 ,
max,
см4
|  ,
max,
см ,
max,
см
| 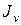 min,
см4
min,
см4
|  min,
см
min,
см
|  ,
см4 ,
см4
|  ,
см ,
см
| |
| b | t | |||||||||||
| 3,05 3,77 | 3,89 4,8 | 9,21 11,2 | 1,54 1,53 | 14,6 17,8 | 1,94 1,92 | 3,8 4,63 | 0,99 0,98 | 5,42 6,57 | 1,38 1,42 | |||
| 5,6 | 3,44 4,25 | 4,38 5,41 | 13,1 16 | 1,73 1,72 | 20,8 25,4 | 2,18 2,16 | 5,41 6,59 | 1,11 1,1 | 7,69 9,41 | 1,52 1,57 | ||
| 6,3 | 3,9 4,81 5,72 | 4,96 6,13 7,28 | 18,9 23,1 27,1 | 1,95 1,94 1,93 | 29,9 36,8 42,9 | 2,45 2,44 2,43 | 7,81 9,52 11,2 | 1,25 1,25 1,24 | 11 13,7 15,9 | 1,69 1,74 1,78 | ||
| 5,38 6,39 | 6,86 8,15 | 31,9 37,6 | 2,16 2,15 | 50,7 59,6 | 2,72 2,71 | 13,2 5,5 | 1,39 1,38 | 18,7 22,1 | 1,9 1,94 | |||
| 7,5 | 5,8 6,89 7,96 | 7,39 8,78 10,1 | 39,5 46,6 53,3 | 2,31 2,3 2,29 | 62,6 73,9 84,6 | 2,91 2,9 2,89 | 16,4 19,3 22,1 | 1,49 1,48 1,48 | 23,1 27,3 31,2 | 2,02 2,06 2,1 | ||
| 7,36 8,51 | 9,38 10,8 | 57 65,3 | 2,47 2,45 | 90,4 104 | 3,11 3.09 - | 23,5 | 1,581,58 | 33,4 38,3 | 2,19 2,23 | |||
| 8,33 9,64 10,9 | 10,6 12,3 13,9 | 82,1 94,3 106 | 2.78 2,77 2,76 | 3,5 3,49 3,48 | 38,9 43,8 | 1,79 1,78 1,77 | 48,1 55,4 62,3 | 2,43 2,47 2,51 | ||||
| 10,8 12,2 15,1 17,9 | 13,8 15,6 19,2 22,8 | 131 147 179 209 | 3,08 3,07 3,05 3,03 | 207 233 | 3,88 3,87 3,84 3,81 | 54,2 60,9 74,1 86,9 | 1,98 1,98 1,96 1,95 | 76,4 86,3 110 122 | 2,71 2,75 2,83 2,91 | |||
| 11,9 13,5 | 15,2 17,2 | 176 198 | 3,4 3,39 | 4,29 4,28 | 72.7 81,8 | 2,19 2,18 | 2,96 | |||||
| 12,5 | 15,5 17,3 19,1 22,7 | 19,7 22 24,3 28,9 | 294 327 360 422 | 3,87 3,86 3,85 3,82 | 4,87 4,86 4,84 4,82 | 122 136 149 174 | 2,49 2.48 2,47 2.46 | 172 192 211 248 | 3,36 3,4 3,45 3,53 |
Продолжение прил. 2
| 19,4 21,5 25,5 | 24,7 27,3 32,5 | 512 602 | 4,34 4,33 4,31 |
|
|
|


