 |
Зависимости между моментами инерции при повороте осей
|
|
|
|
Д а н о: моменты инерции произвольной фигуры относительно координатных осей z, y; угол поворота этих осей  (рис. 3.5). Считаем угол
(рис. 3.5). Считаем угол  положительным при повороте от оси
положительным при повороте от оси 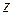 против часовой стрелки.
против часовой стрелки.
О п р е д е л и т ь: моменты инерции фигуры относительно осей z1 и y1, повернутых относительно исходных осей на угол  .
.

Рис. 3.5.
Формулы для определения моментов инерции 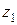 и
и 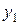 имеют вид:
имеют вид:
 ; (3.10)
; (3.10)
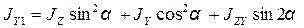 ; (3.11)
; (3.11)
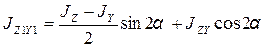 . (3.12)
. (3.12)
Складывая формулы (3.10) и (3.11), получим
 .
.
При повороте осей сумма осевых моментов инерции остаётся постоянной. При этом каждый из них меняется в соответствии с формулами (3.10) и (3.11). Ясно, что при каком–то положении осей моменты инерции будут иметь экстремальные значения: один из них будет наибольшим, другой – наименьшим.
Установлено, что экстремальные значения моментов инерции плоского сечения достигаются относительно главных центральных осей. При этом известно, что центробежный момент инерции относительно этих осей равен нулю. Далее моменты инерции относительно главных осей будем называть главными моментами инерции.
Определение положения главных осей инерции и
Величины главных моментов инерции
Начальную произвольную центральную систему координат z, y надо повернуть на такой угол 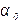 , чтобы центробежный момент инерции стал равным нулю. Приравняв нулю (3.12), получим
, чтобы центробежный момент инерции стал равным нулю. Приравняв нулю (3.12), получим
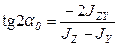 . (3.13)
. (3.13)
Формула для определения моментов инерции относительно главных осей имеет вид:
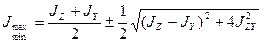 . (3.14)
. (3.14)
Радиусы инерции и моменты сопротивления
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции:
 , (3.15)
, (3.15)
где 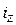 – радиус инерции относительно оси z.
– радиус инерции относительно оси z.
|
|
|
Из выражения (3.15) следует, что
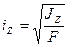 ,
, 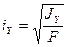 . (3.16)
. (3.16)
Главным центральным осям инерции соответствуют главные радиусы инерции
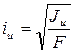 ,
, 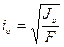 . (3.17)
. (3.17)
Зная главные радиусы инерции, можно графическим способом найти радиус инерции (а, следовательно, и момент инерции) относительно произвольной оси.
Рассмотрим ещё одну геометрическую характеристику, характеризующую прочность стержня при кручении и изгибе – момент сопротивления. Момент сопротивления равен моменту инерции, деленному на расстояние от оси (или от полюса) до наиболее удалённой точки сечения. Размерность момента сопротивления – единица длины в кубе (см3).
Для прямоугольника (см. рис. 3.2) 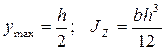 , поэтому осевые моменты сопротивления
, поэтому осевые моменты сопротивления
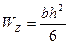 ,
, 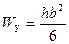 . (3.18)
. (3.18)
Для круга 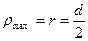 ;
; 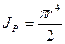 , поэтому полярный момент сопротивления
, поэтому полярный момент сопротивления
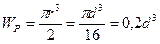 . (3.19)
. (3.19)
Для круга 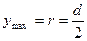 ,
,  , поэтому осевой момент сопротивления
, поэтому осевой момент сопротивления
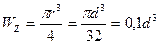 . (3.20)
. (3.20)
З а д а н и е
Для балки, поперечное сечение которой показано на рис. 3.6, необходимо выполнить следующие расчеты.
Часть I. Произвести расчет геометрических характеристик плоского сечения.
1. Определить положение центра тяжести поперечного сечения.
2. Определить положение главных осей инерции.
3. Вычислить значения главных моментов инерции сечения.
4. Вычислить величину главных радиусов инерции, построить эллипс инерции и подсчитать моменты сопротивления.
Часть II. Определить величину допускаемой нагрузки для балки, показанной на рис. 3.7, если известно допускаемое напряжение
 МПа.
МПа.
Исходные данные в соответствии с шифрами взять из табл. 3.1.
Таблица 3.1
| № строки | Схема | H | h | 
| t | Номер профиля | 
| 
| |
| Рис. 3.6 | Рис. 3.7 | мм | м | ||||||
| 1,5 | 1,0 | ||||||||
| 1,6 | 1,1 | ||||||||
| 1,7 | 1,2 | ||||||||
| 1,8 | 1,3 | ||||||||
| 1,9 | 1,4 | ||||||||
| 2,0 | 1,5 | ||||||||
| 2,1 | 1,6 | ||||||||
| 2,2 | 1,7 | ||||||||
| 2,3 | 1,8 | ||||||||
| 2,4 | 1,9 | ||||||||
| е | е | д | д | б | в | е | а | а |
Примечание: каждый номер профиля уголка в сортаменте имеет несколько толщин. При назначении исходных данных можно взять любую толщину.
|
|
|
Пример расчета
Часть 1. Расчет геометрических характеристик плоского сечения
И с х о д н ы е д а н н ы е
Выбираем исходные данные из табл. 3.1, рис. 3.6 и 3.7 согласно индивидуальному шифру студента. В примере рассматриваем схему, показанную на рис. 3.8.

Рис. 3.6.
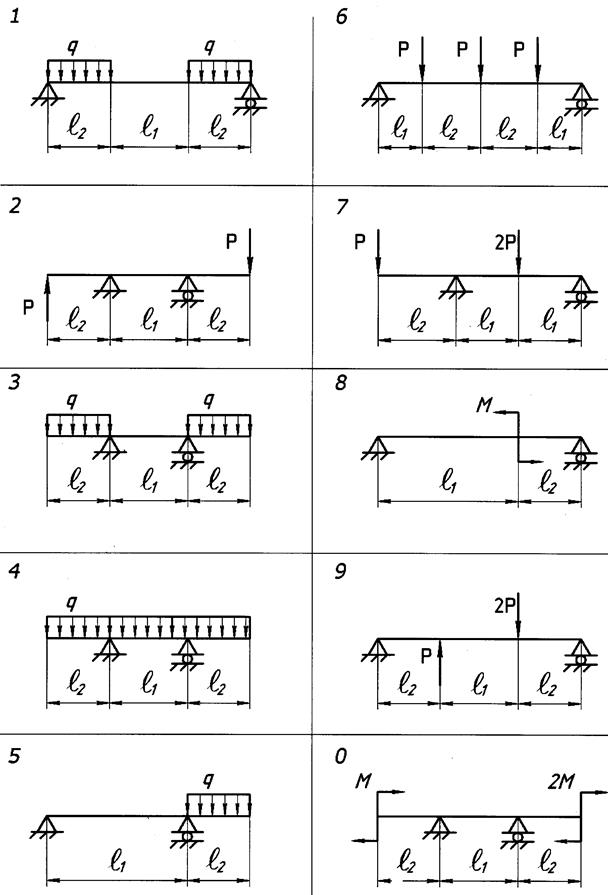
Рис. 3.7.

Рис. 3.8.
Значения величин геометрических параметров и величин для стандартных профилей выбираем из таблицы сортамента (Прил. 2).
| 
|
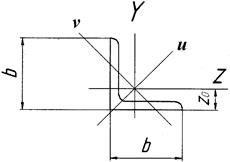
Уголок № 10
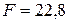 см2 см2
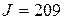 см4 см4
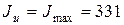 см4 см4
 см4 см4
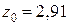 см см
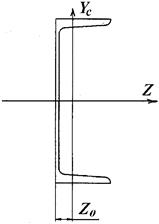
| Швеллер № 30
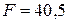 см2 см2
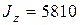 см4 см4
 см4 см4
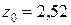 см см
|
Р е ш е н и е
Вычерчиваем схему сечения в масштабе M1:2 (рис. 3.9). Проводим центральные оси фигур, составляющих сечение:  – прямоугольник,
– прямоугольник,  – швеллер,
– швеллер, 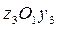 – уголок. При этом оси
– уголок. При этом оси 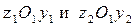 являются главными, а оси
являются главными, а оси 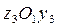 главными не являются.
главными не являются.
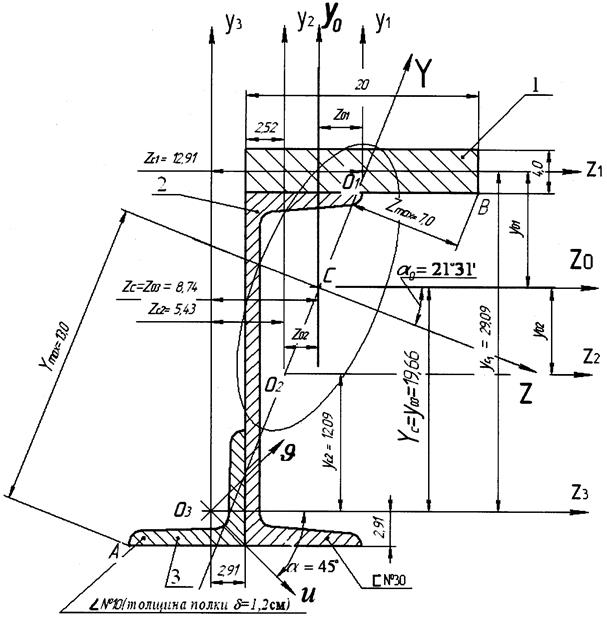
Рис. 3.9.
Примечание: Все линейные размеры в [см].
Таблица 3.2
| № фигуры | Площадь
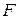 , см2 , см2
| Координаты центров тяжести относительно осей  , , 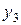 , см , см
| Статические моменты относительно осей z3, y3, см3 | Координаты центров тяжести относительно осей  , ,  , см , см
| |||
| 
| 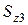
| 
| 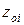
| 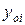
| ||
| I полоса | 80,0 | 12,91 | 29,09 | 2327,2 | 1032,8 | 4,17 | 9,43 |
| II швеллер | 40,5 | 5,43 | 12,09 | 489,6 | 219,9 | -3,31 | -7,57 |
| III уголок | 22,8 | -8,74 | -19,66 | ||||
| 143,3 | 2816,8 | 1252,7 |
Продолжение таблицы 3.2
| № фигуры | Моменты инерции, см4 | ||||||||
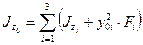
| 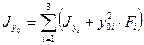
| 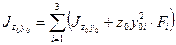
| |||||||
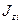
| 
| 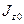
| 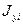
| 
| 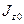
| 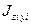
| 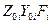
| 
| |
| I полоса | 106,7 | 7220,7 | 2666,7 | 1391,1 | 4057,8 | 3145,8 | 3145,8 | ||
| II швеллер | 232,08 | 8130,8 | 443,7 | 770,7 | 1014,8 | 1014,8 | |||
| III уголок | 8812,6 | 9021,6 | 1741,6 | 1950,6 | 3917,7 | 4039,7 | |||
1. Определяем положение центра тяжести сечения.
В качестве базовых осей, относительно которых подсчитывали статические моменты, приняты оси  и
и  .
.
1.1. Определяем положение центра тяжести по формулам:

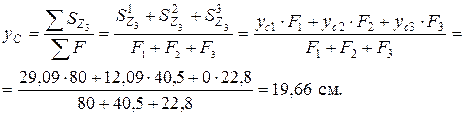
Вычисления можно проводить в табличной форме (см. табл. 3.2).
В столбцы 1-4 заносим данные для расчета, а в столбцы 5-6 – результаты расчета (табл. 3.2).
|
|
|
1.2. Отмечаем на чертеже точку С с координатами  ;
; 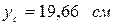 – данная точка является центром тяжести сечения.
– данная точка является центром тяжести сечения.
2. Определяем положение главных осей инерции. Проводим через точку С оси 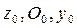 параллельно базовым осям
параллельно базовым осям  Оси
Оси 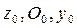 – центральные оси и необходимы для определения положения главных осей инерции.
– центральные оси и необходимы для определения положения главных осей инерции.
2.1. Определяем координаты фигур в новых координатных осях и заносим их в столбцы 7 и 8 табл. 3.2.
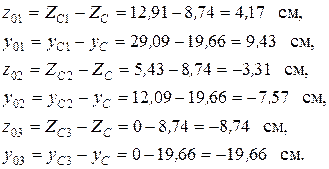
2.2. Определяем значения моментов инерции сечения  относительно центральных осей
относительно центральных осей 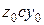 . вычисляем в столбцах 9-17 моменты инерции относительно осей
. вычисляем в столбцах 9-17 моменты инерции относительно осей  При этом момент инерции рассматриваемого элемента сечения относительно оси
При этом момент инерции рассматриваемого элемента сечения относительно оси 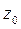 складывается из собственного момента инерции элемента относительно оси
складывается из собственного момента инерции элемента относительно оси 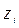 и его переносного момента инерции относительно оси
и его переносного момента инерции относительно оси 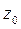 , равного произведению площади данного элемента на квадрат расстояния от его собственной оси
, равного произведению площади данного элемента на квадрат расстояния от его собственной оси 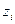 до центральной оси всего поперечного сечения
до центральной оси всего поперечного сечения 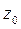 .
.
Следовательно, осевой момент инерции сечения относительно оси 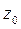 будет равен
будет равен
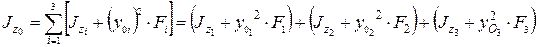 ,
,
где  – собственный момент инерции i -й фигуры;
– собственный момент инерции i -й фигуры;  – переносный момент инерции i -й фигуры.
– переносный момент инерции i -й фигуры.
Прямоугольник имеет собственный момент инерции
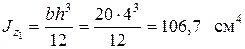 ;
;
 .
.
Для швеллера №30  ,
,  для уголка 100х100х12
для уголка 100х100х12  в соответствии с таблицей сортамента.
в соответствии с таблицей сортамента.
Переносные моменты инерции для прямоугольного элемента, швеллера и уголка равны (см. рис. 3.8 и табл. 3.2).
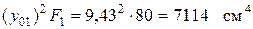 ,
,
 ,
,
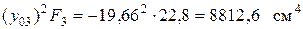 ,
,
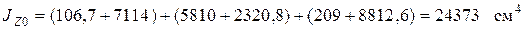 .
.
Аналогично определяются момент относительно оси  и центробежный момент относительно осей
и центробежный момент относительно осей 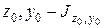 .
.


 .
.
Центробежный момент инерции прямоугольника относительно осей z 1,  у 1 и
у 1 и 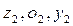 равен нулю, т.е.
равен нулю, т.е. 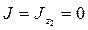 , поскольку оси z 1,
, поскольку оси z 1,  у 1 и
у 1 и 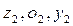 – главные (оси симметрии).
– главные (оси симметрии). 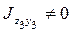 , так как оси
, так как оси 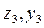 центральные, но не являются главными.
центральные, но не являются главными.
Относительно главных центральных осей инерции центробежный момент инерции равен нулю по определению, а относительно центральных осей, не являющихся главными.
Поэтому для определения 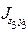 воспользуемся формулой преобразования центробежного момента инерции при повороте осей
воспользуемся формулой преобразования центробежного момента инерции при повороте осей
 .
.
Моменты инерции уголка относительно главных осей берем из таблицы сортамента: J u = 331 см4, J υ = 86,9 cм4, J uυ = 0.
Чтобы ось u совпала с осью Z 3, надо совершить поворот на угол 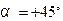 . Положительным углом поворота считается угол поворота против часовой стрелки. Тогда
. Положительным углом поворота считается угол поворота против часовой стрелки. Тогда
|
|
|
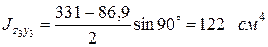 .
.
Получим
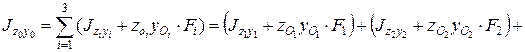

 .
.
При расчете в табличной форме сначала заполняем столбцы 7,8, затем результаты расчетов заносим в столбцы 9-17 (табл. 3.2).
2.3. Определяем положение главных осей инерции всей фигуры
 ;
;
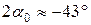 ;
; 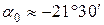 .
.
Откладываем на чертеже угол  в отрицательном направлении, т.е. по часовой стрелке, на рис. 3.9 он показан стрелкой. Сейчас проводим через точку С главные оси Z и Y.
в отрицательном направлении, т.е. по часовой стрелке, на рис. 3.9 он показан стрелкой. Сейчас проводим через точку С главные оси Z и Y.
3. Определяем главные моменты инерции
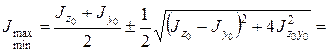
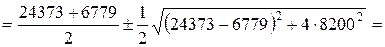
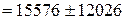 ;
;

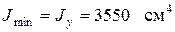 .
.
Для контроля правильности расчетов делаем проверку.
Проверка 1.

Проверка 2.

4. Осуществляем необходимые построения, измерения, вычисления для нахождения:
4.1. Моментов сопротивления. Из чертежа видно, что наиболее удаленными от осей zOy точками являются точки А и В. Линейкой измеряем координаты и отмечаем на чертеже
Y mах = 13,0 см; Z mах = 7,0 см.
Величина моментов сопротивления
 ;
; 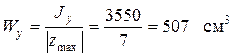 .
.
4.2. Главных радиусов инерции
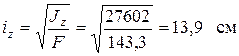 ;
; 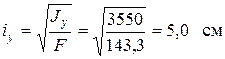 ;
;
4.3. Эллипса инерции
Откладываем значения радиусов инерции вдоль главных осей, причем iz откладываем вдоль оси Y, а iy – вдоль оси Z и на этих отрезках, как на полуосях, строим эллипс (рис. 3.9).
Часть II. Определение допускаемой нагрузки на балку
Р е ш е н и е
Определяем наибольшую допускаемую нагрузку. Для этого сначала строим эпюру моментов (рис. 3.10) и находим значение изгибающего момента в опасном сечении,  . Балку располагаем таким образом, чтобы нагрузка была приложена в плоскости ХOY.
. Балку располагаем таким образом, чтобы нагрузка была приложена в плоскости ХOY.
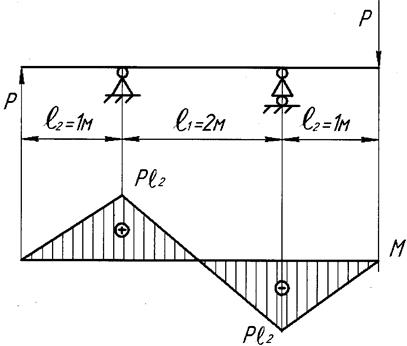
Рис. 3.10.
Величину Р можно определить из условия прочности по нормальным напряжениям
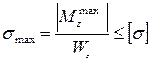 ;
; 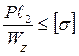 .
.
отсюда
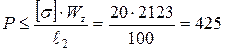 кН,
кН,
где 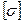 – допускаемое напряжение; Wz – момент сопротивления (ч. I, п. 4.1).
– допускаемое напряжение; Wz – момент сопротивления (ч. I, п. 4.1).
|
|
|


