 |
Способы задания движения материальной точки
|
|
|
|
ВЕКТОРНЫЙ СПОСОБ
Задание зависимости 
(рис. 2).
Радиус-вектор 
изменяется по модулю и направлению.
Рис. 2. Векторный способ задания движения точки
В декартовых координатах проекции будут:
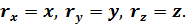
Тогда:
где 
– единичные направляющие векторы (орты).
Конец вектора движется по траектории, называемой годографом этого вектора.
КООРДИНАТНЫЙ СПОСОБ
Используется, когда траектория движения точки заранее неизвестна (рис. 3).
Рис. 3. Координатный способ задания движения точки
в декартовых координатах x, y, z
Задаются отдельные зависимости в декартовых координатах:
Эти уравнения определяют траекторию движения точки в параметрическом виде. Параметр – время 
.
Возможно построение траектории в плоскости в виде зависимости 
, т.е. исключением параметра 
.
Пример.
Дано: 
.
Из первого уравнения выражаем
После подстановки во второе уравнение получаем:
ЕСТЕСТВЕННЫЙ СПОСОБ
Используется, когда траектория движения точки заранее известна, т.е. задаётся (рис. 7).
Рис. 7. Естественный способ задания движения точки
Точка 
– начало отсчёта дуговой координаты 
в зависимости от времени .
Должны быть заданы:
1) траектория;
2) начало и направление движения;
3) закон движения 
ОПРЕДЕЛЕНИЕ ВЕКТОРА СКОРОСТИ
МАТЕРИАЛЬНОЙ ТОЧКИ
Рис. 8. Определение скорости точки
Вектор средней скорости (рис. 8)
направлен по хорде 
.
Значение:
Вектор мгновенной скорости
направлен по касательной к траектории в точке 
.
ОПРЕДЕЛЕНИЕ ВЕКТОРА УСКОРЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
Рис. 9. Определение ускорения точки
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ СКОРОСТИ И УСКОРЕНИЯ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ.
|
|
|
КАСАТЕЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ
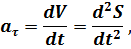
где 
– радиус кривизны траектории,
Рис. 10. Определение полного ускорения
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА.
ОБЩЕЕ ОПРЕДЕЛЕНИЕ И ЗАКОН ЭТОГО ДВИЖЕНИЯ
Поступательное движение твёрдого тела – это такое движение, при котором любая прямая в теле перемещается, оставаясь параллельной своему начальному направлению.
В общем случае траектория такого движения может быть кривой линией (движение спарника, педали велосипеда). Чаще всего – это движение по прямой.
Пример движения спарника.
Движение спарника (рис. 11) – это движение механизма, состоящего из двух кривошипов одинаковой длины 
с балкой 
.
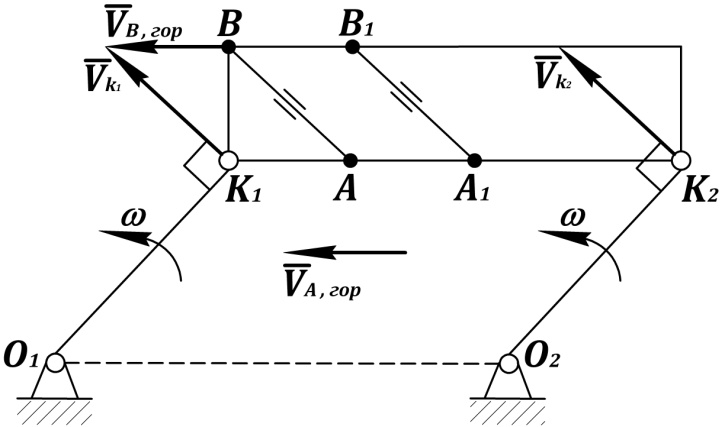
Рис. 11. Движение спарника
Отдельные точки спарника движутся по окружностям вокруг осей 
и 
с угловой скоростью 
, но все линии балки остаются параллельными исходному направлению, т.е. не поворачиваются. Это поступательное движение балки 
с горизонтальной линейной скоростью
Есть и вертикальное поступательное движение.
Закон поступательного движения твёрдого тела: все его точки имеют одинаковые по модулю и направлению скорости и ускорения.
Доказательство (рис. 12)
Рис. 12. Закон поступательного движения твёрдого тела
Для твёрдого тела (балки)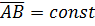 
.
При 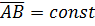получается
тогда
далее
Следовательно, поступательное движение тела определяется движением какой-нибудь одной его точки.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК И ЗАКОНА ЭТОГО ДВИЖЕНИЯ
Вращательное движение твёрдого тела (рис. 13) – это такое движение, при котором какие-нибудь две точки тела остаются неподвижными. Прямая, проходящая через них, называется осью вращения.
Закон вращения
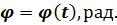
Угловая скорость
Угловое ускорение
При ускоренном вращении величины и 
имеют одинаковые знаки, а при замедленном – разные.
|
|
|
Рис. 13. Вращательное движение твёрдого тела
ОПРЕДЕЛЕНИЕ ЗАКОНА РАВНОМЕРНОГО
ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
отсюда
При 
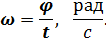
В технике скорость равномерного вращения определяется числом оборотов в минуту: 1 оборот = 2π рад, n оборотов = 2πn рад.
Это происходит за 
, отсюда
|
|
|
