 |
Разложение пространственной силы на
|
|
|
|
ПРОЕКЦИИ ПО ОСЯМ КООРДИНАТ
В плоскости 
(рис. 42)
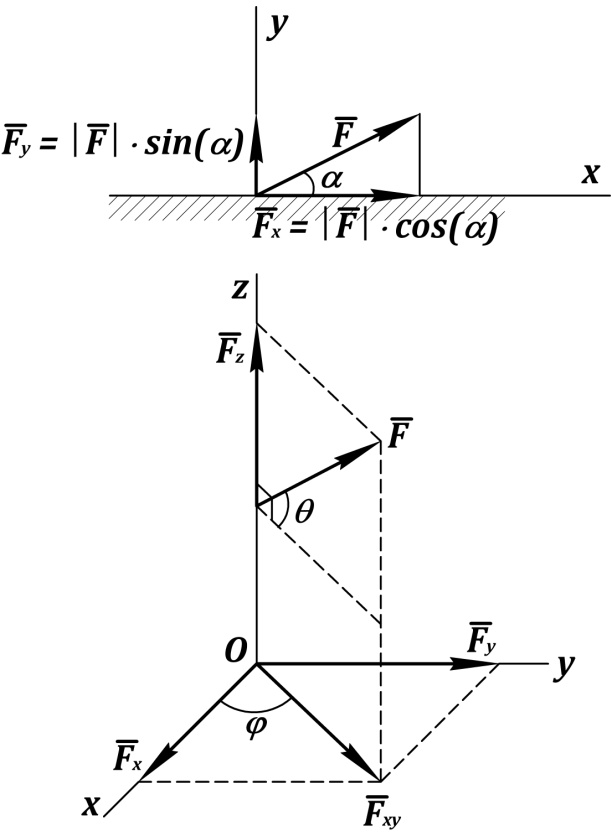
Рис. 42. Разложение одной силы в плоскости
Рис. 43. Разложение одной силы на систему сходящихся сил
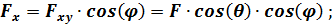
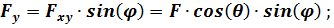
Если известны проекции 
, то значение силы 
будет (рис. 43)
а углы между силой F и её проекциями на оси будут
РАЗЛОЖЕНИЕ ПЛОСКОЙ СИЛЫ ПО СВЯЗЯМ
Кронштейн 
(рис. 44)
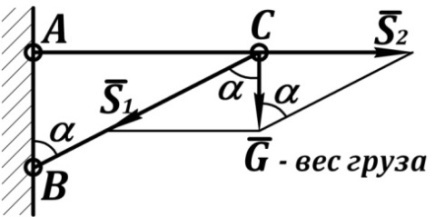
Рис. 44. Разложение силы по связям: кронштейн 
и 
– стержни.
Дано: 
.
Решение:
Сила сжатия стержня
Сила растяжения стержня
Подвес на тросе 
(рис. 45)
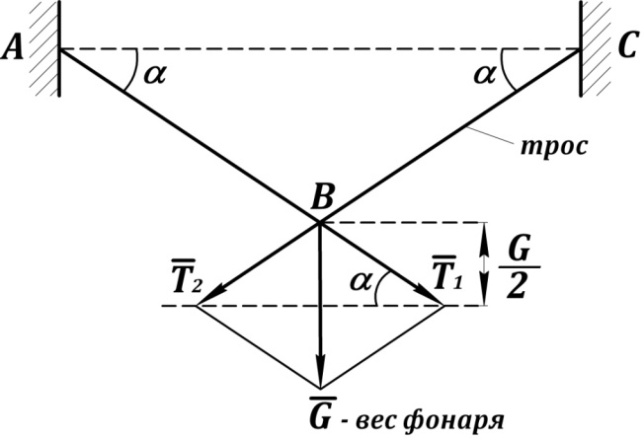
Рис. 45. Разложение силы по связям: подвес на тросе
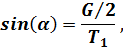
отсюда
Пример. Вытягивание завязшей машины с помощью туго натянутого троса (рис. 46).
Рис. 46. Вытягивание завязшей машины с помощью туго натянутого троса
Нельзя сильно натягивать тросы линий электропередач или бельевые верёвки – могут порваться при обледенении или под весом белья при сушке на ветру.
УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
Геометрическое условие
¾ силовой многоугольник должен быть замкнут.
Аналитическое условие
¾ равнодействующая (главный вектор)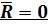 
.
Для пространственной системы из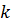 
сил проекции
ТЕОРИЯ МОМЕНТОВ СИЛ
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА
Вектор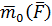 
перпендикулярен плоскости 
; направлен в ту сторону, откуда поворот виден против часовой стрелки (рис. 47а); определяется векторным произведением
модуль вектора
– это площадь параллелограмма со сторонами 
и (рис. 47б).
Свойства момента силы:
1) не изменяется при переносе силы по линии её действия;
2) равен нолю, когда 
или 
.
а)
б)
Рис. 47. Момент силы относительно центра
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
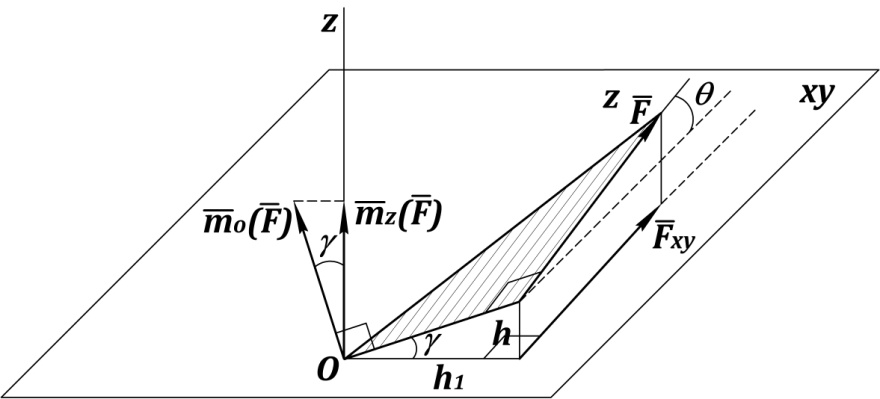
Рис. 48. Момент силы относительно оси
и 
– в пространстве;
|
|
|
и 
– в плоскости 
(рис. 48);
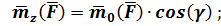
9. АНАЛИТИЧЕСКИЕ ФОРМУЛЫ ДЛЯ МОМЕНТОВ ОТНОСИТЕЛЬНО КООРДИНАТНЫХ ОСЕЙ
ОТ ПРОЕКЦИЙ СИЛЫ
Даны координаты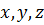 
точки приложения силы и проекций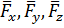 
(рис. 49).
Проекция момента силы на ось 
, как сумма моментов от проекций :
Так как 
параллельна 
, то
Рис. 49. Момент от проекций силы относительно координатных осей
По мнемоническому (от греч. мнемоника (mnemo – память; Мнемозина – богиня памяти) – искусство запоминания путём образования ассоциаций) правилу круговой перестановки индексов и координат против часовой стрелки (рис. 50) получаем
Рис. 50. Правило круговой перестановки индексов и координат
ТЕОРИЯ ПАР СИЛ. ОСНОВНЫЕ ПОНЯТИЯ.
ФОРМУЛИРОВКИ ТЕОРЕМ
– плечо пары сил (рис. 51).
Рис. 51. Пара сил
1. Две пары сил, имеющие одинаковые моменты, эквивалентны.
2. Пару сил можно переносить в плоскость, параллельную данной, не меняя её действия.
3. Система пар сил в пространстве эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар:
ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ
(ПРИВЕДЕНИЕ СИЛЫ К НЕКОТОРОМУ ЗАДАННОМУ ЦЕНТРУ)
Формулировка: силу, приложенную к телу, можно переносить параллельно из данной точки в другую, прибавляя пару сил с моментом, равным моменту переносимой силы до другой точки (рис. 52).
Доказательство:
Рис. 52. Теорема о параллельном переносе силы
и 
– дополнительные силы:
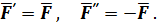
Пара сил и образуют момент 
.
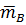В точке 
остаётся сила 
и появляется момент .
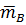ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ
(ПЛОСКОЙ ИЛИ ПРОСТРАНСТВЕННОЙ)
СИСТЕМЫ СИЛ К НЕКОТОРОМУ ЗАДАННОМУ ЦЕНТРУ
В этом случае система сил 
, 
, 
, …, 
заменяется одной силой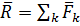 
и суммой моментов, а именно произведений каждой из этих сил на расстояние от точки её приложения до некоторого центра 
Замечания.
1. Сила 
не является здесь равнодействующей, так как заменяет систему сил не одна, а с появившейся парой сил, имеющей момент 
.
|
|
|
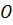2. Значение от выбора центра не зависит, а значение меняется с изменением центра , в который переносятся силы.
ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
|
|
|
