 |
К простейшему виду в случае, когда главный вектор равен нолю, а главный момент не равен нолю
|
|
|
|
Случай 1:  .
.
Система сил приводится к паре сил с моментом  . Значение
. Значение  от выбора центра
от выбора центра 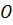 не зависит. Это значение вычисляется по составляющим его проекциям
не зависит. Это значение вычисляется по составляющим его проекциям

ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
К ПРОСТЕЙШЕМУ ВИДУ В СЛУЧАЕ, КОГДА ГЛАВНЫЙ ВЕКТОР НЕ РАВЕН НОЛЮ, А ГЛАВНЫЙ МОМЕНТ РАВЕН НОЛЮ
Случай 2:  .
.
Система сил приводится к равнодействующей  , приложенной в центре
, приложенной в центре 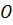 . Значение
. Значение  вычисляется по составляющим её проекциям
вычисляется по составляющим её проекциям

ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
К ПРОСТЕЙШЕМУ ВИДУ В СЛУЧАЕ, КОГДА ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ НЕ РАВНЫ НОЛЮ И ВЕТОР ГЛАВНОГО МОМЕНТА ПЕРПЕНДИКУЛЯРЕН ГЛАВНОМУ ВЕКТОРУ
Случай 3.1:  , причём
, причём 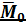 перпендикулярен
перпендикулярен  .
.
Дополнительно можно приложить пару сил  и
и  , по величине равных
, по величине равных  (рис. 53). Тогда силы
(рис. 53). Тогда силы  и
и  уравновесятся (
уравновесятся ( ). Силы
). Силы  и
и  исключены.
исключены.

Рис. 53. Приведение пространственной системы сил
к простейшему виду:
 , причём
, причём  перпендикулярен
перпендикулярен 
Пару сил  и
и  можно было приложить на таком плече
можно было приложить на таком плече  , что они создадут момент равный
, что они создадут момент равный  .
.
В итоге система сил в этом случае приводится к одной равнодействующей 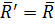 , приложенной в точке
, приложенной в точке  .
.
ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
К ПРОСТЕЙШЕМУ ВИДУ В СЛУЧАЕ, КОГДА ВЕКТОР ГЛАВНОГО МОМЕНТА ПАРАЛЛЕЛЕН ГЛАВНОМУ ВЕКТОРУ
Случай 3.2:  , причём
, причём 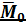 параллелен
параллелен  .
.

Рис. 54. Приведение пространственной системы сил к простейшему виду:
 , причём
, причём  параллелен
параллелен 
 – момент от пары сил
– момент от пары сил  и
и  (рис. 54).
(рис. 54).
Совокупность силы  и пары сил
и пары сил  и
и  называется динамическим винтом с осью
называется динамическим винтом с осью  по линии действия
по линии действия  .
.
ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
К ПРОСТЕЙШЕМУ ВИДУ В СЛУЧАЕ, КОГДА ВЕКТОР ГЛАВНОГО МОМЕНТА И ГЛАВНЫЙ ВЕКТОР НЕ ПЕРПЕНДИКУЛЯРНЫ И НЕ ПАРАЛЛЕЛЬНЫ
Случай 3.3:  , но
, но 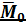 и
и  не перпендикулярны и не параллельны.
не перпендикулярны и не параллельны.
|
|
|
Вектор  можно разложить на составляющие
можно разложить на составляющие  параллельно
параллельно  и
и 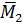 перпендикулярно
перпендикулярно  (рис. 55).
(рис. 55).

Дополнительно можно приложить пару сил  и
и  по величине равных
по величине равных  на таком плече
на таком плече  , что они создадут момент равный
, что они создадут момент равный  .
.

Рис. 55. Приведение пространственной системы сил к простейшему виду:
 , но
, но  и
и  не перпендикулярны и не параллельны
не перпендикулярны и не параллельны
Силы  и
и  исключены.
исключены.
Остаются:
¾ сила 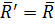 в точке
в точке  на расстоянии
на расстоянии  от точки
от точки 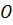 ;
;
¾ момент  , как свободный, перенесённый в точку
, как свободный, перенесённый в точку  .
.
В итоге система сил приводится к динамическому винту с осью, проходящей через точку  .
.
УСЛОВИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ
(ПРОСТРАНСТВЕННОЙ ИЛИ ПЛОСКОЙ) СИСТЕМЫ СИЛ
Необходимо и достаточно, чтобы было  , и относительно любого центра
, и относительно любого центра 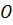 было
было  .
.
Для пространственной системы сил


или, используя проекции на оси координат всех 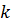 сил и их моментов относительно осей
сил и их моментов относительно осей

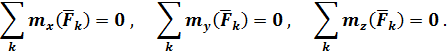
Для плоской системы сил

ТЕОРЕМА ВАРИНЬОНА
Формулировка: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра 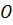 равен сумме моментов сил относительно этого центра (рис. 56).
равен сумме моментов сил относительно этого центра (рис. 56).

Рис. 56. Теорема Вариньона
Доказательство:

Система сил  ,
,  , …,
, …,  заменяется равнодействующей
заменяется равнодействующей  , приложенной в некотором центре
, приложенной в некотором центре  .
.
Если приложить к центру  дополнительную силу
дополнительную силу  , то система будет в равновесии. При этом главный вектор
, то система будет в равновесии. При этом главный вектор  , а при равновесии и главный момент относительно центра
, а при равновесии и главный момент относительно центра 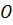 будет
будет  .
.
Можно раскрыть содержание величины 
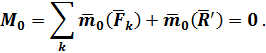
При 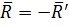

Тогда

что и требовалось доказать.
СЛОЖЕНИЕ ПАРАЛЛЕЛЬНЫХ СИЛ.
ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
Условия равновесия тела (рис. 57):




Рис. 57. Сложение параллельных сил

Рис. 58. Центр параллельных сил
Точка  – центр параллельных сил (рис. 58).
– центр параллельных сил (рис. 58).
Согласно теореме Вариньона в данном случае

или

отсюда

КООРДИНАТЫ ЦЕНТРА СИЛ, ПАРАЛЛЕЛЬНЫХ ОДНОЙ ОСИ

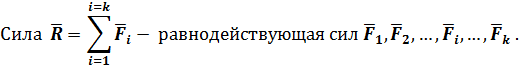
Согласно теореме Вариньона выполняется следующее равенство (рис. 59):
|
|
|

Рис. 59. Координаты центра тяжести

или момент вокруг оси  будет
будет

Отсюда

Аналогично

Если силы повернуть параллельно другой оси, например  , то будет
, то будет

КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ ТЕЛА

Замечание.
Центр тяжести – это точка геометрическая. Она может быть вне тела, например, у кольца.
Для 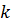 объёмных однородных тел
объёмных однородных тел

где  – удельный вес.
– удельный вес.

Для 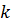 плоских тел с площадями каждого
плоских тел с площадями каждого 

Для 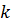 участков однородной пространственной линии
участков однородной пространственной линии

ДИНАМИКА
|
|
|


