 |
Определение положения мгновенного центра ускорений (МЦУ) плоской фигуры относительно мгновенного центра скоростей этой фигуры
|
|
|
|
Рис. 24. Мгновенный центр ускорений плоской фигуры
Исходные данные: направления и значения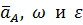 
(рис. 24).
Ранее для равноускоренного вращения было получено (рис. 25)
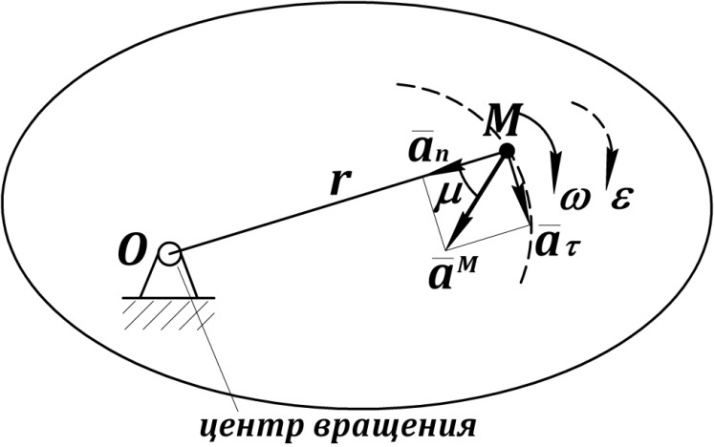
Рис. 25. Вращательное движение точки 
Теперь выполняются следующие действия для определения МЦУ:
1) вычисление угла 
и длины отрезка
2) упреждающее отложение отрезка 
под углом к вектору 
в сторону вращения плоской фигуры при 
(ускоренное вращение) или против вращения при 
(замедленное вращение).
Рис. 26. Определение положения мгновенного центра ускорений
Доказательство того, что точка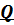 
есть МЦУ, т.е., что 
.
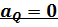Если точка 
полюс вращения, то
где – ускорение поступательного движения полюса ;
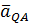– ускорение при вращении вокруг полюса ,
Вектор 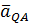, как и ранее вектор 
с линией 
, должен образовывать с линией 
угол , следовательно, вектор 
, но направлен в противоположную сторону, т.е. 
(рис. 26).
Для точки 
в соответствии с выражением (2) получили схему (рис. 27).
Рис. 27. Определение ускорения точки 
После подстановки в выражение (3) выражения для длины отрезка , определённого по формуле (1), получаем по значению
И наконец, при получаем на основе выражения (2)
Что и требовалось доказать.
ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ЛЮБЫХ ТОЧЕК ПЛОСКОЙ ФИГУРЫ ОТНОСИТЕЛЬНО МГНОВЕННОГО ЦЕНТРА УСКОРЕНИЙ ЭТОЙ ФИГУРЫ
На рис. 27 изображено поле ускорений
Рис. 27. Поле ускорений
Для некоторой точки 
будет
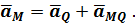
Ранее было получено (3)
Теперь можно записать при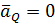 
для точки
Для любых точек плоской фигуры, например, для точки будет подобно
или
СЛОЖНОЕ (СОСТАВНОЕ) ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ
Сложным или составным называют движение материальной точки по отношению к двум системам отсчёта: к основной (условно неподвижной) и к движущейся относительно основной (рис. 28).
|
|
|
Пример: шар катится по палубе движущегося парохода. По отношению к неподвижному берегу движение шара будет сложным.
Рис. 28. Сложное движение точки
1. Относительное движение – движение материальной точки по отношению к подвижной системе отсчёта 
. Относительная скорость 
– по касательной к траектории 
.
2. Переносное движение – движение системы отсчёта по отношению к неподвижной системе отсчёта 
со скоростью 
по касательной к траектории 
. Точка 
неизменно связана с подвижными осями системы отсчёта , с ней в данный момент времени совпадает подвижная точка .
3. Абсолютное движение – движение точки по отношению к неподвижной системе отсчёта со скоростью 
по касательной к траектории 
.
СЛОЖНОЕ (СОСТАВНОЕ) ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ
(ТЕОРЕМА КОРИОЛИСА)
Формулировка: при сложном (составном) движении ускорение материальной точки равно геометрической сумме трёх ускорений: относительного, переносного и поворотного (или кориолисова):
Относительное ускорение вычисляется в обстановке, когда движение самих подвижных осей во внимание не принимается. В подвижной системе отсчёта при естественном способе задания движения по дуге траектории 
будем иметь (рис. 29):
Рис. 29. Относительное ускорение точки
где 
– радиус кривизны траектории.
Переносное ускорение – это ускорение движения подвижной системы отсчёта , т.е. ускорение точки твёрдого тела по отношению к неподвижной системе отсчёта .
В случае ускоренного вращения тела:
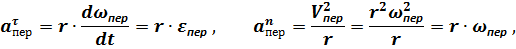
где 
– расстояние от точки до центра 
неподвижной системы отсчета .
Кориолисово (поворотное) ускорение возникает, когда подвижная система отсчёта вращается.
Это ускорение в общем случае имеет векторное выражение:
единица измерения
|
|
|
|
|
|
