 |
Введение в динамику материальной точки. Основные понятия и определения
|
|
|
|
Динамика – описание движения тел под действием сил с учётом инертности масс тел.
Силы:
¾ постоянные;
¾ переменные.
Инертность – свойство тел сохранять движение при отсутствии сил.
Материальная точка – точка, имеющая массу; отвлечение от формы тела, когда оно не вращается.
ЗАКОНЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Первый – закон инерции.
Второй – закон движения под действием сил или закон независимости действия сил:
Третий – закон равенства действия и противодействия.
ДВЕ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
Для свободной точки:
1) основная (прямая): даны силы, определяется закон движения;
2) обратная: дан закон движения, определяются силы.
Для несвободной точки:
1) основная (прямая): даны только активные силы, определяется закон движения и реакции связей;
2) обратная: даны закон движения и активные силы, определяются только реакции связей.
СЛУЧАИ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Рис. 60. Прямолинейное движение материальной точки
Закон движения (рис. 60):
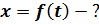
начальные условия:
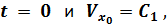
начальные условия:
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ (СВОБОДНОЕ ПАДЕНИЕ БЕЗ УЧЁТА СОПРОТИВЛЕНИЯ)
Рис. 61. Свободное падение материальной точки без учёта сопротивления
Начальные условия (рис. 61):
.
В конечной точке 
при 
:
Уравнение траектории 
получается подстановкой в уравнение 
выражения 
через 
.
ПОНЯТИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА И
РАДИУСА ИНЕРЦИИ ТЕЛА
Момент инерции тела или механической системы (МС), состоящей из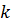 
материальных точек, относительно оси, например, 
– это скалярная величина.
где 
– расстояние от 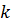- ой точки до оси (рис. 62).
Рис. 62. Момент инерции механической системы относительно оси
|
|
|
Радиус инерции тела, например, относительно оси 
– это величина ρz, определяемая из выражения
Смысл 
– это расстояние от оси до той точки, где сосредоточена вся масса системы 
МОМЕНТЫ ИНЕРЦИИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРАЛЬНЫХ ОСЕЙ
1. Тонкое кольцо радиуса R (рис. 63).
Рис. 63. Момент инерции тонкого кольца
По определению:
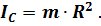
2. Диск (цилиндр) радиуса R (рис. 64).
Рис. 64. Момент инерции диска (цилиндра)
3. Стержень длиной 
и массой 
(рис. 65).
Рис. 65. Момент инерции стержня
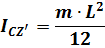
или, если задано 
то
МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСИ,
ПАРАЛЛЕЛЬНОЙ ЦЕНТРАЛЬНОЙ
(ФОРМУЛА ГЮЙГЕНСА-ШТЕЙНЕРА)
Рис. 66. Теорема о моментах инерции относительно параллельных осей
– центр масс; 
– центральная ось; 
– параллельная ось (рис. 66).
ПОНЯТИЕ КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ИЛИ МЕХАНИЧЕСКОЙ СИСТЕМЫ (МС)
1. Для материальной точки – это векторная величина
где 
– по касательной к траектории.
2. Для МС – это векторная величина: главный вектор количеств движения всех точек.
где 
– скорость центра масс.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ИЛИ МС
1. Для материальной точки:
при 
после разделения переменных
и интегрирования получаем:
где 
– элементарный импульс силы.
После интегрирования от 0 до 
получается импульс силы 
:
2. Для МС из 
точек:
После интегрирования от 0 до
ПОНЯТИЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Относительно центра (рис. 67).
Рис. 67. Момент количества движения точки относительно центра
– векторное произведение, где:
– функция момента;
– аргумент функции;
– масса точки.
Абсолютная величина
– площадь прямоугольника со сторонами 
и 
.
Относительно оси (рис. 67).
8. ПОНЯТИЕ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ (КИНЕТИЧЕСКОГО МОМЕНТА)
|
|
|
Относительно центра.
– имя функции,
– аргумент.
2. Кинетический момент при вращении МС (тела) вокруг оси.
Для 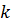-ой точки МС:
где – расстояние от точки до оси 
.
Тогда для отдельной 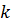-ой точки будет:
где 
– момент;
– количество движения;
– плечо момента.
Известно, что по определению
– момент инерции 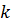-ой точки относительно оси .
Тогда
Для всей МС или тела кинетический момент будет:
9. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Относительно центра.
После дифференцирования по времени получается:
Здесь
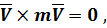
так как и параллельны, т.е. не образуют прямоугольника;
Тогда остаётся
и в итоге получается:
– производная по времени от момента количества движения точки относительно центра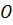 
равна моменту действующей на точку силы.
Относительно оси.
|
|
|
