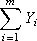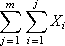Звено второго порядка (колебательное звено)

Такие звенья описываются дифференциальным уравнением вида:

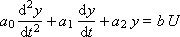
Если на вход звена подать единичную функцию Хэвисайда от времени 1[ t ], при нулевых начальных условиях системы, то реакция на выходе будет называться переходной функцией (или переходной характеристикой), которую часто обозначают как h (t). Сигнал 1[ t ] — это, в некотором смысле, эталонный испытательный сигнал. Существуют и другие эталонные испытательные сигналы. Например, бесконечный импульс нулевой длины (дельта-функция Дирака), гармонический сигнал, периодические прямоугольные импульсы.

Преобразуем по Лапласу это уравнение:

a ₀ · p ² · Y (p) + a ₁ · p · Y (p) + a ₂ · Y (p) = b · U (p)

или, иначе:

(a ₀ · p ² + a ₁ · p + a ₂) · Y (p) = b · U (p).

Определим передаточную функцию звена:

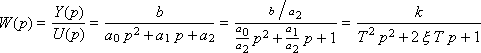
Если записать уравнение без входного воздействия (нулевые входные воздействия U = 0) и сократить Y, то есть: T ² p ² + 2 ξTp + 1 = 0, то такое уравнение будет называться характеристическим, поскольку характеризует исключительно внутренние свойства звена. Обратите внимание, что в записи звена содержатся три параметра:

T — постоянная времени (в секундах); ξ — коэффициент затухания (безразмерная величина); k — передаточный коэффициент.

В зависимости от величины ξ звенья второго порядка классифицируются по видам:

• ξ = 0 — консервативное звено второго порядка;
• 0 < ξ < 1 — колебательное звено второго порядка;
• ξ ≥ 1 — апериодическое звено второго порядка.

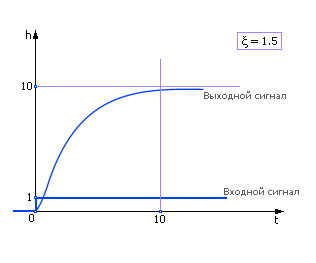
Апериодическое звено 2-го порядка (ξ ≥ 1)

Характеристическое уравнение звена следующее:

T ² p ² + 2 ξTp + 1 = 0.

И оно имеет действительные отрицательные корни:

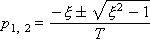
Данное звено можно представить в виде последовательно соединенных звеньев с различными постоянными времени:

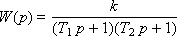
Tогда при T ₁ > T ₂ переходная характеристика звена имеет вид:

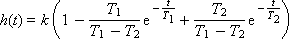
То есть в решении присутствуют затухающие экспоненты. Типичное поведение звена с такими параметрами показано на рис. 4.6.

Рис. 4.6. Реакция апериодического звена на единичный входной сигнал

В частном случае, когда ξ = 1, оба корня будут одинаковыми, отрицательными:

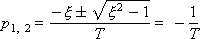
Колебательное звено 2-го порядка (0 < ξ < 1)

Характеристическое уравнение звена следующее:

T ² p ² + 2 ξTp + 1 = 0.

Корни разные, комплексно-сопряженные, с отрицательной вещественной частью:

, где a = – ξ/T, b = sqrt(1 – ξ ²) /T.

Так как корни мнимые, то в поведении звена присутствует колебательная составляющая. Именно за эту особенность поведения звено получило название колебательного (см. рис. 4.7 и рис. 4.8).

Рис. 4.7. Реакция колебательного звена на входной единичный сигнал (ξ = 0.5)

 

Рис. 4.8. Реакция колебательного звена на входной единичный сигнал (ξ = 0.2)

Из графиков видно, что с ростом ξ колебательность звена уменьшается, исчезая при ξ ≥ 1

Переходная функция звена имеет вид:

где

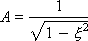
При малых ξ значение A приближается к 1, а значение φ — к 90°. По физическому смыслу ω ₀представляет собой собственную частоту колебаний.

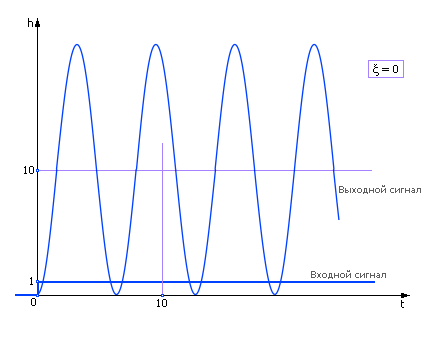
Консервативное звено 2-го порядка (ξ = 0)

Характеристическое уравнение звена следующее:

T ² p ² + 1 = 0.

Корни одинаковые, комплексно-сопряженные, с нулевой вещественной частью:

Так как корни чисто мнимые, то поведением звена являются незатухающие колебания (ξ = 0), см. рис. 4.9.

Рис. 4.9. Реакция колебательного звена на входной единичный сигнал (ξ = 0)

Переходная функция звена имеет вид: h (t) = k · (1 – cos(t / T)).

Из графика экспериментальным путем можно определить единственный параметр T = T ₀/(2 · π).

Динамические регрессионные модели,
заданные в виде передаточной функции

Построим регрессионную модель динамической системы на примере. Зададим модель в виде передаточной функции (см. рис. 5.1).

Рис. 5.1. Модель черного ящика в виде передаточной функции

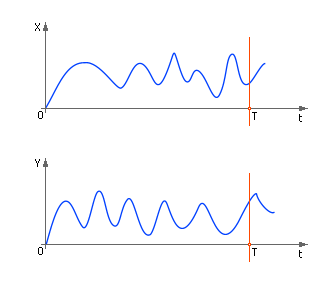
Примерный вид динамических сигналов на входе и на выходе показан на рис. 5.2. Ограничимся временем рассмотрения сигналов, равным T.

Рис. 5.2. Возможный вид зависимости входного сигнала X от времени t и зависимости выходного сигнала Y от t для случая с непрерывным временем

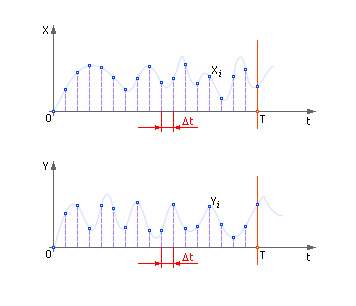
После дискретизации, связанной с обработкой информации на цифровых машинах, эти сигналы будут выглядеть так, как показано на рис. 5.3. Обратите внимание на то, что отдельные отсчеты отстоят друг от друга на расстоянии Δ t. Важно, что отсчеты стоят достаточно часто. Всего этих отсчетов — n, то есть T = n · Δ t,

Рис. 5.3. Возможный вид зависимости входного сигнала X от времени t и зависимости выходного сигнала Y от t для случая с дискретным временем

Допустим, что зависимости, представленные на рис. 5.2 и рис. 5.3, описываются передаточной функцией следующего вида (заметим, что, как и в лекции 02, вид зависимости выдвигается гипотетически и гипотеза должна быть, в конце концов, подтверждена или опровергнута):

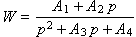
Заменяя значок «p» на «d / dt» (обращаем ваше внимание, что такую замену можно производить только для случая нулевых начальных условий: X (0) = 0 и Y (0) = 0) и учитывая, что передаточная функция — это, по определению, отношение выхода к входу, то есть W = Y / X, получаем дифференциальное уравнение 2-го порядка:

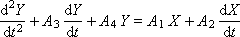
Дважды проинтегрируем это выражение и получим для некоторого произвольного момента времени t:

Коэффициенты A ₁, A ₂, A ₃, A ₄ требуется определить. Для этого выразим уравнение в разностном виде через суммы:

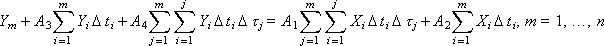
где n — число экспериментальных точек. Заметим, что мы заменили интегралы и непрерывное течение времени — на суммы и дискретное представление времени. Чтобы вычислить суммы и двойные суммы экспериментально заданных зависимостей x и y, воспользуемся для удобства табл. 5.1 (чтобы излишне не загромождать таблицу, мы не стали дописывать в суммах Δ t_i и Δ τ_j).

Таблица 5.1. Таблица исходных данных и вспомогательных расчетов

i Xi Yi   X 1 Y 1 X 1 Y 1 X 1 Y 1   X 2 Y 2 X 1 + X 2 Y 1 + Y 2 2 X 1 + X 2 2 Y 1 + Y 2   X 3 Y 3 X 1 + X 2 + X 3 Y 1 + Y 2 + Y 3 3 X 1 + 2 X 2 + X 3 3 Y 1 + 2 Y 2 + Y 3 … … … … … … … m Xm Ym X 1 + X 2 + … + Xm Y 1 + Y 2 + … + Ym mX 1 + … + Xm mY 1 + … + Ym … … … … … … … n Xn Yn X 1 + X 2 + … + Xn Y 1 + Y 2 + … + Yn nX 1 + … + Xn nY 1 + … + Yn

Ошибку в некоторой m -ой точке можно записать так:

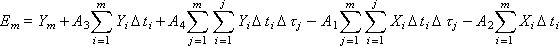
Как и ранее, ошибка показывает, насколько отходит теоретическое значение Y_m от экспериментального значения.

Суммарная ошибка (вносимая всеми точками), которую надо минимизировать, будет:

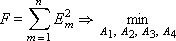
Величина ошибки зависит от значений параметров A ₁, A ₂, A ₃, A ₄. Поэтому F является функцией от четырех переменных: F (A ₁, A ₂, A ₃, A ₄). Чтобы найти минимум функции F, доставляемый за счет параметров A ₁, A ₂, A ₃, A ₄, надо взять частные производные F по каждому из параметров и приравнять каждую производную к нулю. В результате получаем систему линейных уравнений:

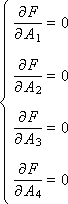
Получено четыре уравнения с четырьмя неизвестными A ₁, A ₂, A ₃, A ₄. Из решения системы уравнений вычисляем неизвестные коэффициенты и дополняем ими модель, где коэффициенты уже определены как числа:

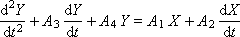
Задача определения коэффициентов модели решена. Разумеется, как и ранее, необходимо сравнить получаемое из этой модели решение Y теоретическое с Y, заданным экспериментально, и вычислить ошибку F. Далее проверить ее значение по критерию — допустимо ли значение вычисленной ошибки, или гипотезу о виде модели требуется сменить на более точную.

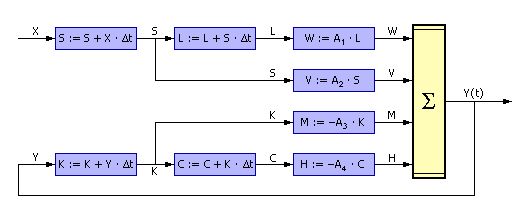
Считая что коэффициенты модели теперь нам известны, построим для заданного примера реализацию, имитирующую поведение системы, описанной передаточной функцией. Для этого воспользуемся уже однажды полученной формулой:

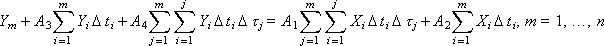
или

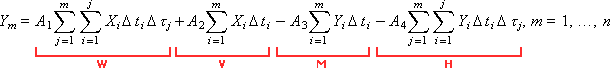
Реализация модели представлена на рис. 5.4.

Рис. 5.4. Техническая реализация передаточного звена после определения коэффициентов регрессионной модели

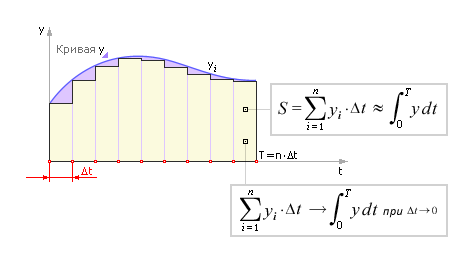
При переходе от интеграла к численному суммированию мы воспользовались методом прямоугольников. Разбив площадь под кривой y на ряд прямоугольников одинаковой ширины Δ t (см. рис. 5.5), получаем, что площадь i -го прямоугольника равна y_i · Δ t, а S — сумма площадей всех n прямоугольников — будет приблизительно равна площади под кривой (интегралу от функции y). Очевидно, что приближение тем точнее, чем меньше значение Δ t.

Рис. 5.5. Применение метода прямоугольников для численного вычисления интегралов

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: