Уравнение состояния рабочего тела

 

Основные параметры состояния рабочего тела (газа) зависят друг от друга и связаны уравнением вида F(υ, p, T) = 0. Зависимость, связывающая между собой параметры состояния, называ­ется уравнением состояния.

Из общего уравнения следует, что для определения состояния тела достаточно знать только два параметра, а третий параметр и все остальные могут быть найдены из уравнения состояния и дру­гих термодинамических зависимостей.

Уравнение состояния для идеального газа выводится на основе молекулярно–кинетической теории газов и имеет вид, для 1 кг газа:

 

Р · υ = R · T.

 

Это уравнение называется характеристическим уравнением или урав­нением Клапейрона.

Величина R – называется газовой постоянной, и для каждого газа имеет свое постоянное значение.

Размерность величины R определяется из выражения:

 

.

 

Если уравнение состояния отнести к т кг газа, оно при­мет вид:

 

 

где V = m · υ – есть полный объем данного количества газа, м³.

Используя приведенные формы уравнения состояния, можно найти любую из величин, входящих в него, если известны или заданы ос­тальные. Для практических расчетов все величины, входящие в урав­нение состояния, следует подставлять в единой системе единиц СИ.

Если уравнение состояния отнести к 1 киломолю газа, то оно становится универсальным уравнением состояния для любого газа:

 

 

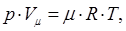
где μ –молекулярный вес газа, 1 киломоль равен μ кг газа;

V_μ – объем 1 киломоля газа, = 22,4 м³/кМоль;

μR – киломольная газовая постоянная.

В соответствии с законом Авогадро при постоянном давлении и температуре 1 киломоль любого газа имеет один и тот же объем. Из уравнения состояния для 1 киломоля газа следует, что если для любого газа величины p, T и V_μ одинаковы, то и величи­на μR имеет одно и то же значение для всех газов.

Поэтому величина μR называется универсальной газовой постоянной, а уравнение состояния для 1 киломоля газа универ­сальным уравнением состояния или уравнением Менделеева–Клапейрона.

Универсальную газовую постоянную можно найти из условия, что при нормальных условиях (t = 0°С, р = 760 мм. рт. ст. или Т = 273,15 К; р = 101330 Па) 1 киломоль любого газа имеет объем V_μ = 22,4 м³, откуда:

 

.

Из условия: ,

можно найти газовую постоянную для любого газа:

 

.

 

Смеси газов

 

В большинстве случаев на практике рабочими телами является не один газ, а смесь нескольких газов, являющихся компонентами смеси. Например: воздух, природный газ, продукты сгорания топли­ва (N₂, CO, CO₂, SO₃, O₂ и т.д.). Поэтому необ­ходимо знать характерные особенности газовых смесей и их законов поведения.

 

1. Общая характеристика смеси газов

Смесь газов – это механическая смесь нескольких идеальных газов, не вступающих в химические реакции друг с другом.

Главный принцип, определяющий свойства газовой смеси, прин­цип независимости действия газов в смеси, т.е. каждый газ в смеси действует независимо от других газов, не меняет своих свойств и подчиняется всем газовым законам.

Кроме того, каждый газ занимает весь объем смеси и все газы в смеси имеют одинаковую температуру, а свойства смеси газов складываются из свойств всех ее компонентов.

Из этого следует, что давление смеси равно сумме парци­альных (частичных) давлений компонентов (закон Дальтона):

 

.

Парциальным давлением называется давление, создаваемое мо­лекулами данного отдельного компонента в газовой смеси. Оно оп­ределяется как давление, которое имел бы данный компонент, если он один занимал бы весь объем смеси при той же температуре.

Парциальное давление вычисляется по уравнению состояния данного компонента:

.

 

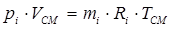Для сравнения газов входящих в смесь по объему вводится понятие парциального объема. Парциальным (приведенным) объемом данного компонента называется условный объем, который имел бы данный компонент, если он один находился при температуре и дав­лении смеси.

Парциальный объем вычисляется по уравнению состояния данно­го компонента:

.

 

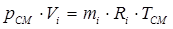Из равенства уравнений состояния следует:

 

.

 

Суммируя полученное уравнение по всем компонентам газовой смеси, получим:

.

 

т. к. по закону Дальтона .

 

2. Способы задания состава смеси

Свойства газовой смеси в первую очередь зависят от ее сос­тава, который может быть задан следующими способами:

– массовая доля – отношение массы компонента к массе смеси:

 

 

– объемная доля – отношение парциального объема компонента к объему смеси:

 

– мольная доля – отношение числа молей компонента к суммар­ному числу молей смеси:

.

 

Т. к. по закону Авагадро объемы 1 киломоля всех газов при нормаль­ных (одинаковых) условиях одинаковы, то можно доказать, что если:

 

 

то есть, последние два способа задания состава эквивалентны.

 

Соотношение между массовой и мольной долей можно найти из уравнения:

.

В итоге имеем следующие соотношения:

 

.

 

В полученных уравнениях μ_СМ – средний (кажущийся) моле­кулярный вес данной газовой смеси, т.е. молекулярный вес такого условного однородного газа, который по своим свойствам аналоги­чен данной газовой смеси.

Исходя из этого, величина μ_СМ определяется по составу смеси следующим образом:

 

 

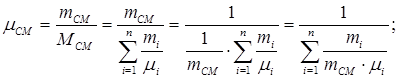
Так как соотношение: .

 

Складывая зависимости для величины g_i по всем компонентам газовой смеси, имеем:

.

 

После преобразований получим:

 

.

 

Уравнение состояния для газовой смеси может быть принято по следующим соображениям. Из принципа независимости следует, что если каждый газ в смеси независимо от других подчиняет уравнению состояния, то и вся смесь может рассматриваться, как один одно­родный газ со своими особыми свойствами, который так же подчиня­ется уравнению состояния, т.е.

.

 

где R_CM – средняя кажущаяся газовая постоянная смеси, опреде­ляемая на основе среднего молекулярного веса смеси:

 

.

 

Величина R_CM может быть также найдена по составу смеси после подстановки зависимостей для μ_СМ:

 

 

Другая зависимость:

 

.

 

Теплоемкость газов

 

Подвод (или отвод) тепла к телу в процессе вызывает измене­ние параметров состояния, главным образом температуры. Поэтому для вычисления количества тепла при изменении состояния тела мож­но использовать изменение температуры и величину, характеризующую свойства тела. Величина, характеризующая способность тела изменять температуру в процессах с подводом (или отводом) тепла называет­ся теплоемкостью.

Теплоемкостью тела называется количество тепла, ко­торое необходимо подвести (или отвести) к телу, чтобы изменить его температуру на 1 К.

Удельной теплоемкостью называется теплоемкость, отнесенная к единице массы вещества.

Понятие теплоемкости используется для вычисления количества тепла участвующего в процессе.

В зависимости от того, к какой единице массы относится тепло­емкость, различают три вида удельной теплоемкости.

Массовой теплоемкостью называется удельная теплоемкость, от­несенная к 1 кг массы газа. Она обозначается С и имеет раз­мерность Дж/(кг· K), кДж/(кг·K).

Объемной теплоемкостью называется теплоемкость, отнесенная к массе газа, содержащегося в 1 м³ газа, взятом при нормальных ус­ловиях. Она обозначается с^/ и имеет размерность Дж/(нм³·К), кДж/(нм³·К).

Киломольной или молярной теплоемкостью называется теплоем­кость, отнесенная к 1 киломолю газа. Она обозначается μС и имеет размерность Дж/(кмоль·K).

Связь между разными видами удельной теплоемкости следующая:

 

 

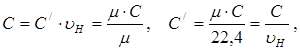
где υ_Н – удельный объем газа, взятого при нормальных усло­виях и равный м³/кг.

Исходя из принятой характеристики удельной теплоемкости, количество тепла в процессе может быть определено по следующим формулам:

 

 

где 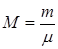– число киломолей рабочего тела;

– объем рабочего тела при нормальных условиях, м³.

Приведенные уравнения справедливы при условии постоянного значения теплоемкости в заданном интервале температур, либо если теплоемкость принимается постоянной условно.

В действительности теплоемкость изменяется в зависимости от вида процесса, в котором участвует газ, а для данного процесса изменяется с изменением температуры. Графическая зависимость теплоемкости от температуры представлена на рисунке 1.1.

 

 

Рисунок 1.1 – Зависимость теплоемкости газа от температуры

Для бесконечно малого участка зависимости С = f(t) истинная теплоемкость при данной температуре тела t, для 1 кг массы может быть определена из условия:

 

откуда: .

При изменении темпера­туры рабочего тела в про­цессе от t₁ до t₂ количество тепла участвующе­го в процессе на 1 кг мас­сы тела будет равно:

 

где, очевидно, что: C = f(t).

Величина истинной теплоемкости, определяется для разных ве­ществ экспериментальным путем и обычно выражается степенной зави­симостью вида:

где a₀, a₁, a₂, a₃ – эмпирические коэффициенты.

Для упрощения практических расчетов по определению количест­ва тепла вводится условное понятие средней удельной теплоемкости тела в данном процессе, которая для 1 кг массы в интервале темпе­ратур от t₁ до t₂ будет равна:

.

 

Использование средней теплоемкости облегчает задачу вычисле­ния количества тепла в процессе, т.к. в этом случае:

 

.

 

Значения средней теплоемкости также определяются экспери­ментальным путем, а для расчетов задаются в виде таблиц или эм­пирических зависимостей.

Так как в практических расчетах может потребоваться значение средней теплоемкости в любом интервале температур, то в таблицах и формулах задается значение средней теплоемкости с фиксированным нижним пределом, равным 0°С, т.е. средняя теплоемкость задается только в интервале температур от 0° до t °С, и может быть использована для расчета количества тепла в любом интервале температур путем следующего преобразования. Из условия следует, что:

 

 

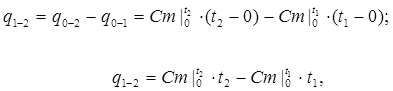
откуда средняя теплоемкость в данном интервале температур равна:

 

.

Величина теплоемкости сильно зависит так же от условий про­текания процесса и для каждого процесса имеет свое определенное значение. При этом ее значение меняется от ± 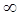(для изотерми­ческого процесса, dT=0) до 0 (для адиабатного процесса, dq=0). Так как число различных термодинамических процессов бесконечно велико, то также велико и число значений теплоемкости в процессах. Для вычисления величины теплоемкости в любом процессе вводятся две основные, стандартные теплоемкости для двух, (принятых за опорные значения) процессов. Это теплоемкость в процессах, протекающих при постоянном давлении, она обозначается С_р и теплоемкость при постоянном объеме – С_υ.

Связь между ними устанавливается уравнением Майера:

С_р – C_υ = R, кДж/кг·К– для 1 кг газа;

 

μC_p – μC_υ = 8,3142, кДж/Кмоль·К – для 1 кмоля.

 

В термодинамике часто используется также отношение:

которое называется коэффициентом Пуассона.

В таблицах и эмпирических формулах для истинных и средних теплоемкостей задаются только два значения теплоемкости С_р или С_υ, a теплоемкость в остальных процессах вычисляется с их помощью в зависимости от характеристики данного процесса.

При обозначениях теплоемкостей учитываются указанные выше обозначения ее видов. Например, μC_υ – истинная, киломольная теплоемкость при постоянном объеме, – средняя, объемная теплоемкость при постоянном давлении и т.д.

Теплоемкость газовых смесей определяется как сумма теплоем­костей входящих в ее состав компонентов с учетом их количествен­ных соотношений.

Для 1 кг смеси газов, массовая теплоемкость будет равна:

 

.

 

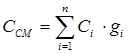Для 1 нм³ смеси газов, объемная теплоемкость будет равна:

 

.

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: