Таблицы и диаграммы состояния водяного пара

Для практических расчетов параметров состояния воды и водя­ного пара во всех трех областях используют два вида таблиц сос­тояния и одну диаграмму состояния – i –S.

1. Таблицы состояний воды и водяного пара

Таблица состояний "Вода и пар на линии насыщения" исполь­зуется для определения параметров состояния влажного пара в об­ласти II при заданном значении величины x и одного из параметров состояния (обычно Р_н или Т_н).

Таблица строится по изменению величины Р_н от 0 до P_к или Т_н от 0 до T_к. Для каждого значения этих параметров указывается соответствующее ему значение параметров состояния по пограничным кривым (при X = 0 – V', i', S'), а при X = I -V"_,i ", S'' и величина удельной теплоты парообразования r.

В промышленной теплоэнергетике для описания свойств воды и водяного пара на линии насыщения ипользуется два вида таблиц:

– первый вариант таблиц (по температурам), в которых в первом столбце указывается температура насыщения Т_н ;

– второй вариант таблиц (по давлениям), в которых в первом столбце указывается давление насыщения Р_н.

Таблица 1.1 свойств воды и водяного пара на линии насыщения (по температурам) представлена ниже.

Таблица состояний "Вода и перегретый пар" используется для определения состояния воды, недогретой до кипения в области I и перегретого пара в области III по задаваемым двум независимым па­раметрам состояния. Эта таблица построена по параметрам Р и Т, как наиболее широко применяемым на практике и доступным для практических измерений.

 

Таблица 1.1 – Свойства воды и водяного пара на линии насыщения

 

TН	РН	V'	i'	S'	V"	i "	S"	r
20
.
.
. TH . . . . .
.
.

 

 

Интервал изменения давления Р – от 0 до 30 ÷ 50 МПа (300 ÷ 500 атм), а температуры Т – от 0 до 500 ÷ 1000 °С, в зависимости от полноты таблицы. Таблица эта информационно насыщенная, так как для каждого сочетания Р и Т в ней даются три остальных параметра (V,i и S).

Величина внутренней энергии вычисляется по ним из уравнения:

 

U = i – p× V.

 

Свойства "Вода и перегретый пар" представляют в виде таблицы 1.2.

Параметры, соответствующие состоянию воды, определяются из условия Т < Т_П, а для перегретого пара Т > Т_Н.

Поэтому, в таблице каждый столбец заданного давления раз­делен на две части: верхняя, где Т < Т_Н – состояние воды; нижняя, где Т > Т_П – состояние перегретого пара.

 

Таблица 1.2 – Свойства ненасыщенной жидкости и перегретого пара

 

 

Так как с ростом давления Т_Н увеличивается, то в таблице получается ступенчатая ло­маная линия, выше которой расположена область состояния воды, а ниже – перегретого пара. При Р > Р_К эта линия отсутствует, так как нет различий между паром и водой.

2. Диаграмма состояний водяного пара – i – S

Эта диаграмма охватывает область перегретого пара и часть области влажного пара около верхней пограничной кривой, которые наиболее часто используются в практических расчетах.

Структура диаграммы, остажающей состояния водяного пара приведена на рисунке 1.11.

На диаграмму нанесены линии постоянных параметров состояние:

– изобары (Р = const) – сплошные черные линии;

– изохоры (V= const) – пунктирные черные линии (или красные линии);

– изотермы (t = const) – сплошные черные линии, начинаю­щиеся от верхней пограничной кривой x=1.0 и идущие в области перегретого пара, в области влажного пара (вниз от линии Х=1,0) изотермы совпадают по направлению с изобарами и поэтому не нано­сятся на диаграмму;

– линии постоянной сухости влажного пара (x = const) – сплошные черные линии в области II, под пограничной кривой.

 

 

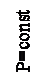Рисунок 1.11 – Диаграмма состояний водяного пара

1.4.5 Термодинамические характеристики и физико-математическое описание процессов влажного воздуха

 

Практически все процессы вентиляции и кондиционирования связаны с атмосферным воздухом, который является влажным воздухом, т. к. в атмосферном воздухе всегда присутствуют водяные пары. Сумма парциальных давлений газовых компонентов смеси равна полному давлению смеси (закон Дальтона):

Р = Р₁ + Р₂ +... + Р_i = åР_i.

Влажный воздух, в первом приближении, можно рассматривать как бинарную смесь, состоящую из водяного пара и приведенного однородного газа - сухой части атмосферного воздуха, эффективная молекулярная масса которого m_в = 29 кг/кМоль. Тогда барометрическое давление влажного воздуха, определяется как давление смеси газов:

 

Р_в = Р_св + Р_п,,

 

где Р_св, Р_п – парциальные давления сухого воздуха и водяных паров.

Давление насыщенного водяного пара является функцией только температуры и может быть определено по таблице.

Температуры водяного пара и сухого воздуха одинаковы и равны температуре влажного воздуха. Компоненты влажного воздуха занимают объем, равный объему всей смеси. Парциальное давление каждого компонента смеси определяется уравнением Клапейрона (с достаточной для технических расчетов точностью можно считать, что влажный воздух подчиняется законам смеси идеальных газов):

р_i = m_i R_i T / V,

где m_i – масса i-того газа;

R_i – газовая постоянная i-того газа;

Т – температура газа;

V – объем газа.

Влажный воздух называется ненасыщенным, если его температура больше температуры насыщенного пара, соответствующей парциальному давлению водяных паров. При этом пар во влажном воздухе перегретый.

Влажный воздух называется насыщенным, если его температура равна температуре насыщения при данном парциальном давлении водяных паров. Эта температура влажного воздуха называется температурой точки росы.

Если температура воздуха станет меньше температуры точки росы, то излишняя влага будет выделяться из воздуха (конденсироваться) в виде тумана, росы, а парциальное давление водяных паров и температура насыщения будут снижаться. На диаграмме TS (рисунок 1.12) в точке 1 показано состояние влажного воздуха при температуре Т и парциальном давлении водяных паров Р_п. В точке 2 на правой пограничной кривой будет состояние насыщенного влажного воздуха при том же парциальном давлении водяного пара и температуре насыщения Т_н (температура точки росы). В точке 3 состояние насыщенного влажного воздуха достигается за счет повышения парциального давления водяных паров до давления насыщения Р_н (например, увлажнением воздуха) при постоянной температуре Т.

Абсолютной влажностью воздуха называется масса водяного пара содержащегося в одном кубическом метре влажного воздуха. Она численно равна плотности пара при его парциальном давлении Р_п и температуре Т.

Относительной влажностью воздуха называется отношение его абсолютной влажности при данной температуре и парциальном давлении пара (Т и Р_п) к максимально возможной абсолютной влажности при той же температуре и давлении насыщения Р_н.

 

 

Относительная влажность выражается в процентах:

 

j = r_п / r_н 100% = Р_п / Р_н 100%,

 

т. к. из уравнения состояния при Т = const следует, что Р_п / Р_н = v_н/ v_п= r_п / r_н.

При обработке влажного воздуха в аппаратах изменяется количество водяных паров, содержащихся в воздухе, а содержание сухого воздуха остается постоянным. Поэтому удобно использовать единицу измерения, выражающую отношение переменного количества влаги к постоянной массе сухого воздуха.

Влагосодержанием называется масса водяного пара, приходящаяся на 1 кг сухого воздуха:

d = m_п / m_с.в = r_п 10³ / r_с.в = m_п р_п / (m_св р_св), г / кг сух.. возд.

 

Из уравнения состояния для каждого компонента газовой смеси, получим:

m_п / m_св = Р_п R_св / (R_п Р_св) = m_п Р_п / (m_св(Р_в - Р_п)) =18 Р_п / (29(Р_в - Р_п)),

т. к. Р_св = Р_в - Р_п,

 

d = 0,622 Р_п / (Р_в - Р_п).

 

Используя уравнения r_в = r_св + r_п, получаем:

 

r_в = r_св (1 + d / 1000).

Удельную теплоемкость влажного воздуха относят к единице массы сухой части воздуха:

с_в = с_св + с_п d/1000 = 1,005 + 1,8068 d*10 ^-3.

Энтальпию влажного воздуха также относят к единице массы сухого воздуха:

 

I = c_в t + 2500 d*10 ^-3 = 1,005 t + (2500 + 1,8068 t) d *10 ^-3 .

 

1.4.6 I-d диаграмма влажного воздуха

Для практических расчетов процессов и состояния влажного воздуха используется I-d – диаграмма влажного воздуха, предложенная Л. К. Рамзиным. Диаграмма построена в косоугольной системе координат для увеличения полезной части диаграммы. Угол между осями I и d составляет 135^о (150^о). На диаграмме (рисунок 1.13) нанесены следующие линии постоянных параметров: I, d, t, j.

Кроме того, на диаграмме нанесены линии постоянной температуры для мокрого термометра t_м =const.

Когда ненасыщенный воздух соприкасается с поверхностью тонкой пленки воды, то происходит тепломассообмен, т. е. будет переноситься тепло и влага в направлении более низкого потенциала. Если температура ненасыщенного воздуха окажется выше температуры воды, а температура воды – выше температуры точки росы, то перенос тепла будет происходить от воздуха к поверхности воды, а перенос влаги – от поверхности воды в воздух. Температура воздуха будет понижаться, а отдаваемое тепло будет затрачиваться на испарение влаги. Испарившаяся влага поступит в воздух, увеличив его влагосодержание и парциальное давление водяных паров. Поступающие в воздух водяные пары за счет своей энтальпии восстанавливают энтальпию воздуха примерно до начальной величины, поскольку отданное воде явное тепло возвращается обратно в воздух в скрытом виде (энтальпия пара). Такой процесс испарения называется адиабатическим. Энтальпия влажного воздуха в начальном состоянии будет равна:

 

I₁ = 1,005 t₁ + 2500 d₁ *10^-3+ 1,8068 t₁ d₁ *10^-3,

 

а в конечном насыщенном состоянии (при j = 100%)

 

I₂ = 1,005 t_м + 2500 d_н*10^-3+ 1,8068 t_м d_н *10^-3 = I₁ + (d_н -d₁) t_м c*10^-3.

Так как I₂ отличается от I₁ на величину начальной энтальпии испарившейся воды, имеющей малую величину, то с достаточной точностью можно считать процесс адиабатическим, т. е. I₂»I₁.

 

 

 

Первое и второе слагаемые характеризуют переход явного тепла в скрытое, а третье слагаемое изменяется незначительно, т. к. с уменьшением температуры одновременно увеличивается влагосодержание.

Температура, которую принимает насыщенная воздушно-паровая смесь в процессе испарения при условии сохранения постоянной энтальпии воздуха, равной начальному, называется температурой мокрого термометра.

Идеальный адиабатический процесс возможен только при t_м = 0 ^оС.

Связь между температурой сухого и мокрого термометров можно установить следующим образом. Количество тепла, которое необходимо для испарения влаги в количестве dx кг/кг сух. возд., будет равно:

 

dq = (r_м + c_п (t_с - t_м)) dx,

где r_м – теплота испарения при температуре мокрого термометра;

c_п – теплоемкость водяного пара.

Это тепло получено при адиабатическом процессе испарения из окружающего воздуха, т. е.

 

dq = с_см dt = - (c_в + c_п x) dt,

где c_в – теплоемкость сухого воздуха;

х – влагосодержание воздуха.

Тогда (r_м + c_п (t_с - t_м)) dx = - (c_в + c_п x) dt.

Интегрируя обе части равенства по х и t в пределах от х до х_м и от t_с до t_м, получим:

,

 

где х_м – влагосодержание насыщенного воздуха при температуре мокрого термометра.

Таким образом, температура мокрого термометра является функцией температуры воздуха и его влагосодержания. Эта формула показывает, что при полном насыщении воздуха, когда х = х_м температура его t_с = t_м.

Значения величины t_м для этих линий определяют по шкале температур сухого термометра, в точке пересечения линии t_м = const с линией j = 100 %.

В нижней свободной части диаграммы нанесена линия зависимости Р_п=f(d), позволяющая определять парциальное давление водяных паров.

Используя диаграмму, можно выполнять следующие определения:

– по заданному на диаграмме положению точки состояния влажного воздуха определять все параметры состояния;

– по заданным двум любым параметрам состояния определить положение на диаграмме точки, определяющей состояние влажного воздуха и значения недостающих параметров;

– по заданным условиям построить и рассчитать любой процесс с влажным воздухом.

1.4.7 Процессы тепловлажностной обработки воздуха

 

а) Процессы тепловлажностной обработки влажного воздуха изображаются на I-d диаграмме прямыми линиями (рисунок 1.14).

Нагрев воздуха. Нагрев воздуха в поверхностных теплообменных аппаратах происходит при d=const (процесс 1–2). Относительная влажность воздуха при нагреве от t₁ до t₂ снижается от φ₁ до φ₂ и его ассимилирующая способность увеличивается.

Расход тепла на нагрев 1 кг воздуха:

 

q _1-2 = I₂ - I₁, кДж/кг

 

Охлаждение воздуха. Охлаждение воздуха до температуры выше температуры точки росы (t_тр), происходит также при постоянном влагосодержании (процесс 1-2'). При охлаждении до температуры ниже температуры точки росы процесс идет по линии φ =100%, а влагосодержание воздуха уменьшается (d₃ < d₁).

Расход холода на 1 кг воздуха:

 

q _1-3 = I₁ - I₃, кДж/кг

 

Смешивание воздуха. Смешивание двух потоков воздуха происходит по линии, соединяющей точки, характеризующие состояние воздуха. Параметры смешанного воздуха определяются тепловлажностным балансом (из условия подобия):

 

L ₁ d₁ + L ₄ d₄ = L d₅; L ₁ I₁ + L ₄ I₄ = L I₅,

 

где L = L ₁ + L ₄ – расход смешанного воздуха;

L ₄, L ₁ – расходы воздуха с параметрами (4) и (1).

б) Тепло- и влагообмен между воздухом и водой

Уравнение теплообмена между воздухом и водой при непосредственном контакте определяется из уравнения теплового баланса, при условии отсутствия теплообмена с окружающей средой:

 

L(I₁-I₂)=Wc_w(t_wк-t_wн),

 

где W – расход воды, вступающей в контакт с воздухом;

c_w – удельная массовая теплоемкость воды;

t_wк, t_wн – температура воды на выходе и входе в аппарат.

Разделив обе части уравнения на L, получим:

 

I₁-I₂= c_w(t_wк-t_wн) W/L= μ c_w(t_wк-t_wн).

 

Отношение W/L=μ называется коэффициентом орошения и показывает, какое количество воды, приходится на 1 кг воздуха.

Интенсивность теплообмена между воздухом и водой зависит от температуры воздуха по мокрому термометру. Зависимость энтальпии воздуха от его температуры по мокрому термометру можно представить в следующем виде:

 

I₁-I₂= 0,7 c_w(t_м1-t_м2),

 

где t_м1, t_м2 – температура воздуха по мокрому термометру на входе и выходе аппарата.

Передача теплоты при явном теплообмене (q_я) может происходить при разности температур путем теплопроводности, конвективного теплообмена и излучением, причем теплопроводностью и излучением можно пренебречь. Скрытый теплообмен (q_с) определяется теплотой парообразования (r). Тогда полное количество теплоты:

 

q_п=q_я+q_с, =α_к (t_в-t_w) + rβ (d_в-d_w)= β (I_в-I_w),

 

где β – коэффициент влагообмена;

β (d_в-d_w)=W_о – количество испаренной влаги.

В результате получаем уравнение, определяющее угловой коэффициент прямой, проходящей через точку (в), характеризующую начальное состояние воздуха и через точку (w), характеризующую состояние воздуха при температуре воды t_w и относительной влажности воздуха φ =100 %:

q_п/ W_о= (I_в-I_w)/ (d_в-d_w) = ΔI/Δd = ε.

 

Возможные направления процессов взаимодействия воздуха с водой представляются линиями, расположенными в области криволинейного треугольника АБВ, у которого одной стороной является кривая φ =100 %, а двумя другими – касательные к этой кривой проведенные из точки А, характеризующей начальное состояние воздуха. В зависимости от температуры воды процессы взаимодействия воздуха и воды изображаются линиями, расположенными в различных областях, отделенных характерными линиями (см. рисунок 1.15):

 

 

Рисунок 1.15:

 

– t_w = t_А – температура воды равна температуре воздуха по сухому термометру (линия t_А = const);

– t_w = t_м – температура воды равна температуре воздуха по мокрому термометру (линия t_м = const или I_А = const);

– t_w = t_тр – температура воды равна температуре точки росы (линия d_А = const).

Область А-Б-1 – характеризуется условием t_w > t_А (в том числе, при увлажнении воздуха паром).

Область А-1-2 – характеризуется условием t_А > t_w > t_м.

Область А-2-3 – характеризуется условием t_м > t_w > t_тр.

Область А-3-В – характеризуется условием t_w < t_тр.

 

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: