Второй закон термодинамики и анализ

ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ

 

Второй закон термодинамики. Основные определения

 

Первый закон термодинамики утверждает положение об эквива­лентности перехода тепловой энергии в механическую и обратно и устанавливает количественные соотношения между изменениями раз­личных форм энергии в системе, но не раскрывает условий и направления протекания процессов взаимопревращения различных видов энергии.

Второй закон термодинамики, так же как и первый, установлен из опыта наблюдений за явлениями природы и основан на следующих опытных положениях.

1. Тепло может переходить самопроизвольно только от более нагретых тел к телам менее нагретым. Обратный процесс требует затраты энергии, подводимой извне.

2. Механическая энергия (работа) всегда может быть превра­щена в тепловую полностью и без остатка, но превращение тепловой энергии в механическую работу может быть осуществлено только частично, при этом, остаток тепла должен быть возвращен в окружающую среду при более низкой температуре.

Из этих и других положений и был сформулирован второй закон термодинамики, устанавливающий условия, при которых происходит превращение тепловой энергии в механическую работу.

Тепловая энергия, сообщенная рабочему телу в процессе, не мо­жет быть полностью превращена в механическую работу. В этом процессе получения механической энергии из тепловой, часть тепловой энер­гии, полученной телом от окружающей среды при более высокой тем­пературе, должна быть отдана в окружающую среду при более низкой температуре.

Термодинамические циклы

Рассмотрим практические условия получения механической энер­гии из тепловой. Преобразование теплоты в работу в термодинами­ческом процессе может быть осуществлено только при расширении рабочего тела, пределы которого ограничены по величине и по вре­мени. Для непрерывного получения работы необходимо периодически после расширения возвращать рабочее тело в исходное состояние путем сжатия.

Такой термодинамический процесс, в котором рабочее тело после нескольких, последовательно протекающих процессов расшире­ния и сжатия, проходит несколько различных состояний и воз­вращается в исходное состояние называется круговым термодинами­ческим процессом или термодинамическим циклом.

Цикл называется обратимым, если состоит из обратимых процес­сов и наоборот. В термодинамике рассматривают два основных вида цикла: прямой и обратный, различающиеся соотношением между рабо­той полученной при расширении и работой, затраченной на сжатие.

1. Прямой цикл

Рассмотрим произвольный прямой цикл в диаграммах p – υ и Т – s, (Рисунок 1.5). Для получения полезной работы, этот цикл осуществляется так, чтобы работа расширения в нем была больше чем работа, зат­раченная на сжатие. Для этого требуется, чтобы при сжатии рабочего тела от него осуществлялся отвод тепла.

 

 

 

 

Рис. 1.5 – Произвольный прямой Рисунок 1.6 – Произвольный обратный

цикл цикл

При расширении газа в процессе 1–2 совершается работа L _1, при подводе тепла q₁. При обратном сжатии газа 2–1 затрачи­вается работа L _2, и отводится тепло q_2.

При этом, по условию L ₁> L ₂, a q₁ > q₂. Разность L ₁ – L ₂ = L – есть полезная работа, отданная во внешнюю среду, a q₁ – q₂ = q, - тепло, полученное от внешней среды и прев­ращенное в работу. При этом, т.к. рабочее тело возвращается в исходное состояние, то в результате осуществления цикла не происхо­дит изменения внутренней энергии рабочего тела.

На основании первого закона термодинамики, примененного к циклу q₁ – q₂ = U + L ₁ – L ₂, т.к. по правилу знаков для 1–го закона термодинамики q₁ > 0; q₂< 0и L ₁ > 0; L ₂ < 0, а изменение внутренней энергии отсутствует, т.к. в цикле рабочее тело возвращается в исходное состояние, т.е. U = 0.

Тогда q₁ – q₂ = L ₁ – L ₂ ; q = L.

Из анализа диаграммы T – S, при сравнении площадей под линиями подвода и отвода тепла, следует, что средняя температура в процессе подвода тепла T ₁cpбольше, чем средняя темпера­тура в процессе отвода тепла T₂ cp.

Суммируя полученные выводы можно записать следующее опреде­ление.

Термодинамический цикл, в котором:

– работа, полученная при расширении больше, чем работа, затраченная при сжатии, и избыток полезной работы отдается в ок­ружающую среду;

– подведенное тепло больше, чем отведенное тепло и разность их есть тепло, превращенное в полезную работу;

– средняя температура в процессах подвода тепла всегда выше средней температуры процессов отвода тепла;

– в диаграммах p – V и T – sпроцессы идут по часовой стрелке,

называется прямым циклом или циклом теплового двигателя.

Основная цель прямого цикла – получение полезной работы за счет затраты тепла, подводимого извне.

 

2. Обратный цикл

Сущность обратного цикла состоит в том, что для передачи тепловой энергии от источника с низкой температурой к источнику с более высокой температурой необходимо повысить температуру ра­бочего тела, получившего тепловую энергию при низкой температуре. В обратном цикле это осуществлено путем сжатия, таким образом, чтобы работа сжатия была больше работы расширения, а избыток зат­раченной работы пошел на увеличение внутренней энергии (и темпе­ратуры) рабочего тела. В результате этого тепловая энергия может быть отдана в окружающую среду при более высокой температуре.

Рассмотрим произвольный обратный цикл в диаграммах р – V и T – s, (Рисунок 1.6).

При расширении газа в процессе 1–2 совершается полезная ра­бота L₂ и подводится тепло q₂ .

При обратном сжатии газа 2–1 затрачивается работа, в результате чего увеличивается внутренняя энергия газа, его тем­пература и количество тепла, отводимое в окружающую среду q₁ > q₂.

Разность L ₁ – L ₂ = L есть затраченная на осуществление цикла работа, полученная из окружающей среды, a q₁ – q₂ = q –тепло, в которое превращается эта работа в цикле. По первому закону тер­модинамики для обратного цикла с учетом правила знаков имеем:

– q₁ + q₂ = 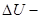L₁ + L₂;

 

так как для цикла 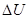= 0,то: – q₁ + q₂ = – L₁ + L₂; – q = – L; q = L.

 

Сравнивая в диаграмме T – S площади под линиями подвода и отвода тепла, получим, что средняя температура подвода тепла меньше, чем средняя температура отвода тепла

Суммируя полученные выводы можно дать определение обратного цикла.

Термодинамический цикл, в котором:

– работа, полученная при расширении меньше, чем работа, зат­раченная при сжатии, и избыток затраченной работы подводится из окружающей среды;

– подведенное тепло меньше, чем отведенное тепло и избыток отведенного тепла образуется за счет превращения в тепло затра­ченной работы;

– средняя температура в процессах подвода тепла всегда ниже, чем средняя температура в процессах отвода тепла;

– в диаграммах p – V и T – S процессы идут против часовой стрелки,

называется обратным циклом или циклом холодильной машины.

Основная цель обратного цикла – отвод тепла от тел с низкой температурой и передача этого тепла в окружающую среду с высокой температурой за счет затраты работы, подводимой извне.

3.2.3. Характеристики эффективности термодинамических циклов

Эффективность любого цикла характеризуется коэффициентом эффективности, который равен:

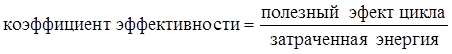
С увеличением эффективности цикла увеличивается и этот коэф­фициент.

Для прямых циклов характеристика эффективности называется термическим коэффициентом полезного действия, который равен:

По второму закону термодинамики и в соответствии с определением всегда _t<1_.

Для обратных циклов характеристика эффективности называется холодильным коэффициентом, который равен:

 

т. е. эффективность обратного цикла определяется количеством тепла, отведенного при низкой температуре и затраченной работой.

 

Цикл Карно

Осуществление обратимого цикла, требует подвода и отвода тепла при бесконечно малой разности температур, а следовательно, в процессах с изменением температуры необходимо иметь бесчислен­ное множество источников и приемников тепла. Только в изотерми­ческих процессах источник (или приемник) тепла будет один.

При этом, если остальные процессы будут адиабатические может быть осуществлен обратимый цикл при наличии только одного источника и одного приемника тепла с постоянными температурами T₁ и T₂. Этот цикл был предложен Карно, который доказал, что КПД цикла наибольший из всех циклов осуществляемых между температурами T₁ и T₂.

1. Прямой цикл Карно

Прямой цикл Карно представлен на рисунке 1.7 и состоит из двух изотерм и двух адиабат.

 

 

 

Рисунок 1.7 – Прямой цикл Карно

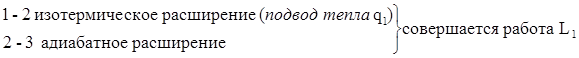
Термический КПД прямого обратимого цикла Карно (диаграмма Т – S):

 

_Т.К. S₁ = S₄; S₂ = S₃ .

 

Анализ выражения КПД цикла Карно показывает, что эффективность этого цикла возрастает с увеличением температуры подвода тепла – T₁ и уменьшением температуры отвода тепла – T₂. Однако, КПД ни­когда не будет равен 1, т. к. T₂ не может быть равным нулю, а T₁ – бесконечности. При достижимых предельных значениях этих тем­ператур равных (T₁)_max= 1500÷2000 K, а (Т₂)_min= 300 К, значение КПД цикла Карно не превышает _t = 0,8 ÷ 0,85.

Из полученного выражения следует, что термический КПД цикла Карно зависит только от температур T₁ и Т₂ и не зависит от свойств рабочего тела. Это положение называется теоремой Карно и доказывается от противного.

2. Обратный цикл Карно

Рассматривая аналогичным образом обратный цикл Карно, в ко­тором подвод тепла q₂ происходит при температуре Т₂, отвод тепла q₁, при температуре Т₁, а на осуществление цикла за­трачивается работа L= q₁- q₂, получим выражение для холо­дильного коэффициента обратного цикла Карно:

.

Анализ полученного выражения показывает, что эффективность обратного цикла Карно возрастает с уменьшением разности T₁ – T₂ для чего следует по возможности уменьшать температуру T₁ и увеличивать T₂.

3. Эквивалентный цикл Карно

Покажем, что цикл Карно имеет КПД больший, чем у любого цикла, протекающего в тех же пределах температур. Рассмотрим в T – S – диаграмме произвольный цикл a b c d, протекающий в пределах температур T₁ и T₂ , и представленный на рисунке 1.8.

Опишем цикл Карно 1,2,3,4,1 в тех же пределах температур. Сравнивая коли­чество тепла в T – S – диаграмме получим > и < , тогда из выражения КПД следует: .

 

Рисунок 1.8 – Эквивалентный цикл Карно

В пределе и 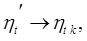т.е. интер­вале температур T₁ и Т₂ цикл Карно является идеальным циклом, имеющим наибольший КПД.

Заменим переменное значение темпе­ратуры подвод тепла в произволь­ном цикле (процесс а,в,с) среднеинтегральной постоянной температурой подвода тепла T_KP`, которая определяется из условия:

 

 

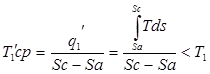
Соответственно, заменим переменную температуру отвода тепла (процесс c, d, а) среднеинтегральной постоянной температурой отвода тепла Т_2cp, определяемой из условия:

.

 

 

Построим цикл Карно 1,2,3,4,1 в пределах температур 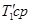и и разности энтропий S₂` – S<sub>1</sub>` = Sc – Sa. B соответст­вии с определением понятия среднеинтегральной температуры, коли­чества подведенного и отведенного тепла в этом цикле Карно будут равны соответствующим количествам тепла в произвольном цикле по равенству:

 

 

Из этого следует, что К.П.Д. цикла Карно, осуществленного между температурами и , будет равен КПД произвольного заданного цикла:

.

 

Такой цикл будет называться эквивалентным циклом Карно, т.е. эффективность эквивалентного цикла Карно равна эффективности произвольного цикла.

Практически важным выводом из этого является то, что для увеличения КПД произвольного цикла и приближения его к КПД цик­ла Карно, необходимо повышать среднюю температуру в процессе подвода тепла, приближая и понижать среднюю температу­ру в процессе отвода тепла, приближая , тогда .

Практическое значение цикла Карно состоит в том, что он является критерием для определения степени совершенства любого произвольного цикла, а также может быть использован для анализа сравнительной эффективности любых произвольных циклов, путем замены их соответствующими эквивалентными циклами Карно.

В действительности цикл Карно не может быть осуществлен, вследствие ряда практических трудностей.

 

 

ВОДЯНОЙ ПАР

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: