Исследование частных случаев политропного процесса

 

Исследование выполняется на основе уравнений общего, полит­ропного процесса в следующей последовательности:

– на основе общей характеристики процесса для данного част­ного случая определяется значение величины теплоемкости процесса;

– по величине теплоемкости процесса вычисляется значение показателя политропы, соответствующее данному частному случаю;

– подставляя полученные значения теплоемкости и показателя политропы в уравнения общего термодинамического процесса, получим все необходимые уравнения, характеризующие данный термодинами­ческий процесс, как частный случай общего процесса;

– по полученным уравнениям этих процессов в диаграммах p – υ и T – S наносятся линии процессов в указанных диаграммах. Для большей наглядности p – υ и T – S – диаграмм, где на концах линий процессов указывается соответствующее значение показателя политропы, в одинаковых процессах обозначены:

– процесс с подводом тепла (1–2);

– процесс с отводом тепла (1–2^/ ).

Графический анализ термодинамических процессов представлен на рисунке 1.4.

1. Исследование изохорного процесса

Условие протекания изохорного процесса υ = const, откуда следует, что C = C_V.

Подставляя значение теплоемкости в уравнение 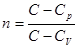, получим .

 

Подставляя полученные значения и C = C_V в уравнение общего процесса, получим:

– уравнение изохорного процесса в диаграмме р – υ из р · υⁿ = const, или p^1/n · υ = const, чтопри , дает выражение υ = const;

– уравнение изохорного процесса в диаграмме T – S из S = C · ln T+A, что при C = C_V дает выражение S = C_V · ln T+A;

– соотношение параметров в изохорном процессе (при ; С = С_V и υ₁ = υ₂):

; (закон Шарля)

 

 

– работа и тепло в изохорном процессе из уравнения q = C · (T₂ – T₁) при C = C_V определяются по уравнениям:

 

;

 

из уравнения при , имеем l_V = 0.

 

 

Рисунок 1.4 – Графический анализ термодинамических процессов

Линия процесса (изохора) прямая, параллельная оси p в диаграмме p– υ и логарифмическая кривая в диаграмме T – S.

 

2. Исследование изобарного процесса

Условие протекания изобарного процесса p = const, откуда следует, что: C = C_p.

Подставляя значение теплоемкости в зависимость для n, получим n = 0.

Подставляя значения n = 0 и C = C_p в уравнение общего процесса, получим:

– уравнение изобарного процесса в диаграмме p – υ из p · υⁿ = const, при n = 0 имеем p = const;

– уравнение изобарного процесса в диаграмме T – S, из S = C ·ln T+A, при C = C_p имеем S = C_p ·ln T+A;

– соотношение параметров в изобарном процессе (при n = 0; C = C_p; p₁ = p₂ = p):

; (закон Гей-Люссака)

;

– работа и тепло в изобарном процессе:

 

.

 

Линия процесса (изобара) – прямая, параллельная оси υ в диаграмме p – υ и логарифмическая кривая, проходящая менее круто, чем изохора, в диаграмме T – S.

3. Исследование изотермического процесса

Условия протекания изотермического процесса T = const, откуда следует, что: dT = 0 и .

Подставляя значение теплоемкости в уравнение показателя политропы

получим п=1.

Подставляя значения п=1 и в уравнение общего процесса, получим:

– уравнение изотермического процесса в диаграмме р – υ из условия, что р · υ^п = const и n = 1 представляет собой симметричную гиперболу

 

;

 

– уравнение изотермического процесса в диаграмме T – S из условия, что S = C · ln T+A и S/C = ln T+A при представляет собой горизонтальную прямую, параллельную оси S ();

– соотношение параметров в изотермическом процессе:

; (закон Бойля-Мариотта)

; ;

 

– это неопределенность, тре­бующая вывода нового уравнения для разности S₂ – S₁ в изотермическом процессе;

– работа и тепло в изотермическом процессе:

– это неопределенность, требующая вывода нового уравнения для вычисления количества тепла q_T в изотерми­ческом процессе;

– это неопределенность, требующая вывода нового уравнения для вычисления количества работы в изотермическом процессе.

Вывод нового уравнения работы в изотермическом процессе выполняем исходя из общего выражения dl = p · dυ, следовательно:

.

Из уравнения изотермы в диаграмме p – υ имеем:

 

.

 

Подставляя последнее выражение p в подинтегральное выражение, получим:

.

 

Используя уравнение состояния и уравнение соотношения параметров, получим различные виды уравнения работы в изотермическом процессе:

 

 

Из уравнения первого закона термодинамики для изотермического процесса следует, что q_T = u₂ – u₁ + l_T, но т.к. u₂ – u₁ = 0, то:

 

Из выражения дифференциала энтропии для условий изотермичес­кого процесса (T = const) следует:

– если то при T = const, интегрируя, имеем

,

откуда:

 

Кривая процесса (изотерма) представляет собой равнобокую гиперболу в диаграм­ме р – υ и прямая, параллельная оси S, в диаграмме T – S.

4. Исследование адиабатного процесса

Условие протекания процесса dq = 0, т.е. тепло не под­водится и не отводится, откуда следует, что C = dq/dt = 0. Подставляя значение теплоемкости в уравнение получим: ,

где k – показатель адиабаты, который имеет значение от 1,3 до 1,6.

Подставляя значения и C = 0 в уравнение общего процесса, получим:

– уравнение адиабатного процесса в диаграмме p – υ, которое из условия p · υ^п = const и при n = k имеет вид несимметричной гиперболы (p · υ^k = const);

– уравнение адиабатного процесса в диаграмме T – S, которое из условия S = C ·ln T + A и при С = 0 представляет собой вертикальную прямую (S = A = const), т.е. адиабатный процесс – это одновременно и изоэнтропийный процесс;

– соотношение параметров в адиабатном (изоэнтропийном) процессе: (при n = k; C = 0 u S₁ = S₂):

 

;

 

– работа и тепло в адиабатном процессе:

q_A = 0;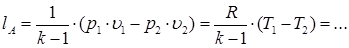

Из приведенного анализа следует, что соотношение параметров, работа, изменение внутренней энергии и энтальпии, аналогичны политропному процессу при значении n = k.

Кривая процесса (адиабата) представляет собой неравностороннюю гипербола в диаграмме p – υ и прямую, параллельную оси T в диаграмме T – S.

 

1.2.9 Анализ общих характеристик политропных процессов в диаграммах p – υ и T – S

Все политропные процессы, представленные на рисунке 4, по основным характеристи­кам делятся на следующие виды.

1. Процессы расширения, в которых совершается полезная рабо­та, отводимая в окружающую среду (dυ>0 и dl>0), и процессы, сжатия, в которых затрачивается работа, подводимая из окружающей среды (dυ<0 и dl<0).

Границей между процессами расширения и сжатия служит изохора ().

2. Процессы с подводом тепла (dS>0 и dq>0) и процессы с отводом тепла (dS<0 и dq<0).

Границей между процессами подвода и отвода тепла служит адиабата (n = k).

3. Процессы с увеличением внутренней энергии рабочего тела (dT>0 и dU>0) и процессы с уменьшением внутренней энергии (dT<0 и dU<0).

Границей между процессами увеличения и уменьшения внутренней энергии служит изотерма (n = 1).

В соответствии с вышеизложенным принято разделять все политропные процессы расширения и сжатия на 3 группы (Рисунок 4).

Первую группу составляют политропные процессы, имеющие зна­чение n в пределах .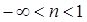

Процессы расширения в первой группе имеют следующие характеристики: dυ>0; dS>0; dS>0 и, следовательно, l>0; q>0 и ∆U>0, т.е. подводимое тепло в этих процессах рас­ходуется на совершение работы и увеличение внутренней энергии рабочего тела.

Процессы сжатия в первой группе имеют характеристики: dυ<0; dS<0; dT<0 и, следовательно, l<0 и q<0; ∆U<0, т.е. уменьшение внутренней энергии и затрачен­ная работа, взятая из окружающей среды, расходуются на тепловую энергию, отводимую в окружающую среду.

Вторую группу составляют политропные процессы, имеющие показатель п в пределах 1<n<k.

Процессы расширения во второй группе имеют следующие характеристики: dυ>0; dS>0; dT<0 и, соответственно, l>0; q>0 и ∆U<0, т.е. работа в этих процессах совершается счет уменьшения внутренней энергии рабочего тела и тепловой энергии, подводимой извне.

Процессы сжатия во второй группе имеют характеристики: dυ<0; dS<0 и dT>0 и, соответственно, l<0; q<0, и ∆ U>0, т.е. работа сжатия, подводимая извне, затрачивается на увеличение внутренней энергии рабочего тела и тепло, отводимое в окружающую среду.

Третью группу составляют политропные процессы, имеющие показатель n в пределах .

Процессы расширения в третьей группе имеют характеристики: dυ>0; dS<0; dT<0, откуда l>0; q<0; ∆U<0, т.е. в этих процессах внутренняя энергия расходуется на полезную ра­боту и тепло, отводимые в окружающую среду.

Процессы сжатия в третьей группе имеют характеристики: dυ<0; dS>0; dT>0, откуда l<0; q>0; ∆U>0, т.е. в этих процессах увеличение внутренней энергии происходит за счет работы сжатия и тепловой энергии, подводимых извне.

В теплотехнике, в тепловых двигателях, наибольшее примене­ние имеют политропные процессы второй группы.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: