Исследование общего термодинамического процесса

 

1. Основные определения и условия исследования

Общим термодинамическим процессом называется процесс проте­кающий при одновременном изменении всех параметров состояния. Такой процесс в термодинамике называется политропным.

Исследование проводится на основе первого закона термоди­намики, уравнения состояния и характеристики параметров состоя­ния U, i и S.

Задача исследования термодинамического процесса состоит в следующем:

– вывод уравнения процесса в p – υ и T – S – диаграммах;

– установление зависимости между параметрами состояния в начале и в конце процесса;

– определения величины изменений внутренней энергии, эн­тальпии и энтропии;

– определение количества работы и тепла в процессе.

Все процессы считаются обратимыми. Для упрощения задачи все процессы принято считать протекающими при постоянной теплоемкос­ти (С), которая для каждого отдельного процесса имеет строго определенное значение, но в общем случае, для разных процессов может принимать значения от до .

Частными случаями политропного процесса являются процессы, протекающие при постоянном значении одного параметра состояния и переменных значениях всех остальных параметров. К ним относят­ся следующие процессы:

– изохорный процесс, протекающий при постоянном объеме;

– изобарный процесс, протекающий при постоянном давлении;

– изотермический процесс, протекающий при постоянной температуре;

– адиабатный процесс, протекающий при отсутствии теплообмена с внешней средой (т.е. dq = 0), при этом dS = 0 и энтропия не меняется, т.е. процесс является изоэнтропийным (S = const).

Изучение этих процессов имеет большое теоретическое и прак­тическое значение в технике.

2. Вывод уравнения политропного процесса в p – υ – диаграмме

Рассмотрим произвольный, бесконечно малый участок политроп­ного процесса, для которого можно записать два выражения уравне­ния первого закона термодинамики в дифференциальной форме, обра­зующих систему дифференциальных уравнений:

.

 

Используя понятие постоянной теплоемкости политропного про­цесса (С) и выведенные в п. 2.6 выражения для dU и di, будем иметь:

 

dq = C · dT; dU = C_υ · dT; u di = C_p · dT.

 

Подставляя эти выражения в систему дифференциальных урав­нений, получим:

C · dT = C_V · dT + p · dυ;

 

C · dT = C_p · dT – υ · dp.

 

Перенося члены уравнения, содержащие дифференциал dT в левую часть и разделив второе уравнение на первое, получим:

 

,

 

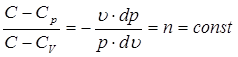где 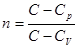– постоянная величина, называемая показатель политропы.

В свою очередь, теплоемкость политропного процесса может быть выражена через показатель политропы таким образом:

 

где .

 

Величины n и С являются основными характерис­тиками политропного процесса и определяют все его свойства. При этом, для характеристики политропного процесса достаточно задать только одну величину n или С, вторая может быть най­дена из приведенного уравнения связи между ними.

Разделяя переменные в полученном дифференциальном уравнении, и интегрируя, получим:

где N – постоянная интегрирования.

Постоянная интегрирования определяется обычно по начальным и конечным граничным условиям процесса.

Так как уравнение политропного процесса справедливо для всех точек процесса, в том числе и для первой и последней точки процесса, постоянная интегрирования будет равна:

Уравнение политропного процесса в p – υ – диаграмме предс­тавляет неравнобокую гиперболу.

3. Вывод уравнения политропного процесса в T – S – диаграмме

Для бесконечно малого участка политропного процесса изме­нение энтропии равно:

.

 

Используя значение постоянной теплоемкости политропного процесса (С), получим:

.

 

Интегрируя последнее выражение, имеем:

 

,

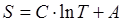где А – постоянная интегрирования, определяемая, обычно, по начальным условиям. Используя значения параметров T и S в начальной или конечной точке процесса, найдем постоянную интег­рирования:

 

 

откуда .

 

Тогда уравнение политропы можно записать в виде:

 

.

 

Уравнение политропного процесса в T – S – диаграмме представляет логарифмическую кривую.

4. Зависимость между начальными и конечными параметрами состояния p, υ и T в процессе

Исходными уравнениями для вывода зависимостей являются уравнения состояния и уравнение политропы для начальной и конечной точки процесса: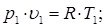

 

Разделив первое уравнение состояния на второе, получим общее уравнение связи между параметрами p, υ, T:

.

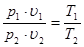Из уравнения политропы получим зависимость между начальным и конечным давлением и объемом:

 

.

 

Подставляя отношение давлений в общее уравнение, получим:

 

.

 

Аналогично, подставляя отношение объемов, будем иметь:

 

.

 

Подученные выражения могут быть использованы для определения неизвестного параметра, либо для вычисления показателя n.

5. Определение изменения величин u, i, S

Используя выражения, выведенные в п. 2.6 для определения энергетических параметров, получим формулы их изменения в процессах:

– для изменения внутренней энергии в процессе (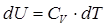), интегрируя, получим:

 

– для изменения энтальпии в процессе () интегрируя, будем иметь:

;

 

– для изменения энтропии в процессе () с учетом, что (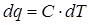), по итогам интегрирования, получим:

 

.

 

Заменяя отношение температур, отношением других параметров, можно выразить ∆ S_1–2 через изменение других параметров.

6. Определение количества тепла в процессе

Из выражения dq = С · dТ, в результате интегрирования получим:

.

 

7. Определение количества работы в политропном процессе

Из выражения dl = p · dυ, интегрируя в пределах от 1 до 2, получим:

 

где .

 

Выразим функцию давления p = f(υ) из уравнения политропного процесса в p – υ – диаграмме:

Откуда давление будет равно:

 

.

 

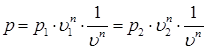Подставляя в подинтегральное выражение полученное значение р, будемиметь:

 

.

 

Преобразуем полученное выражение с целью упрощения:

 

.

 

Используя уравнение состояния идеального газа, получим:

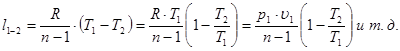
⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: