Процессы истечения и дросселирования газов и паров

 

1.5.1 Основные закономерности истечения газов

 

Турбинные двигатели (составляющие большую часть мощных тепловых двигателей) работают за счет преобразования кинетической энергии рабочего тела в механическую энергию вращения рабочего колеса (ротора) турбинных двигателей.

Возрастание кинетической энергии происходит при ускорении потока в процессах расширения газа с уменьшением давления, осуществляемых в специальных суживающих каналах, называемых соплами. Обратный процесс, торможение потока газа, происходит в расширяющихся каналах, называемых диффузорами.

Для получения расчётных уравнений истечения рассмотрим:

– уравнение I-го закона термодинамики для потока газа:

 

;

 

– уравнение Ньютона:

 

_расп;

 

– уравнение неразрывности (сплошности) потока:

 

, т. е. .

 

Рассмотрим равновесие элементарного объёма потока газа в канале переменного сечения между сечениями I и II (рисунок 1.16).

Для упрощения примем следующие условия движения потока:

– условие установившегося движения, т.е. неизменность всех параметров по времени;

– условие неразрывности потока;

– условие однородности потока, т.е. постоянство всех параметров во всех точках поперечного сечения потока;

– условие отсутствия сил трения;

– условие отсутствия изменения потенциальной энергии положения (неизменность пьезометрических высот).

 

 

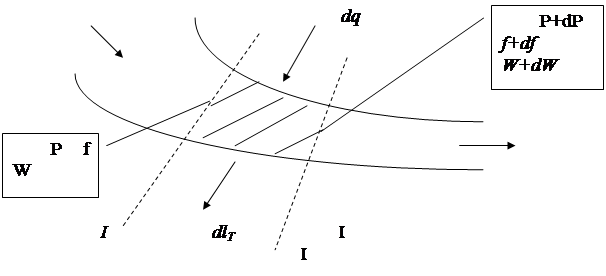
Рисунок 1.16

Тогда в общем случае, если к данному элементарному объёму подводиться количество тепла dq и им совершается полезная работа, отдаваемая во внешнюю среду dl_T (техническая работа), то известное уравнение I-го закона термодинамики для 1 кг газа (уравнение сохранения энергии) примет вид:

 

 

где – работа совершаемая против внешних сил (работа проталкивания);

– изменение внешней кинетической энергии данного объёма газа.

Работа проталкивания равна алгебраической сумме работ внешних сил, действующих в сечениях I и II. За время, равное I сек, элементарная величина равна дифференциалу изменения работы внешних сил в сечениях I и II. Эта работа определяется произведением силы, действующей в сечении (pf) на путь (W), т. е. произведением параметров , характеризуемых для этих сечений. Из изложенного следует:

 

или для расхода m=1кг/с рабочего тела:

 

.

 

Подставляя, получим уравнение I-го закона термодинамики для потока газа с расходом m=1 кг/с:

;

;

.

 

Для частного случая адиабатного сечения газа (или пара) в канале без совершения работы (т. е. dq=0 и dl_Т=0) имеем уравнение I-го закона в таком виде:

 

 

Это уравнение используют при расчёте процессов истечения газа в соплах диффузорах.

Кинетическая энергия потока газа всегда может быть превращена в полезную работу и поэтому называется располагаемой работой:

 

dl _расп = ;

 

При dl_T=0, используя равенства dq=di-vdp

и ,

получим: dl _расп = = dq – di =-vdp.

Разные знаки приращения dw и dp ( =-vdp) показывают, что при dp<0 dW>0 WdW =-Vdp, т. е. скорость растёт при уменьшении давления и наоборот.

Интегрируя полученные уравнения для процесса расширения газа от состояния 1 до состояния 2, получим:

 

l _расп = q+i₁-i₂= .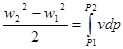

Из дифференциального уравнения политропы в диаграмме pV следует:

 

,

откуда:

l _расп=

 

но, т. к. работа расширения газа в процессе равна:

 

l _расш=

то l _расш=n* l _расш

Следовательно, располагаемая работа в n раз больше работы, получаемой при простом расширении газа в политропном процессе. Для частного случая адиабатного течения газа dq=0 и n=k, получим:

dl _расп= =-di.

Интегрируя от состояния 1 до состояния 2, получим:

 

l _расп= = i₁ -i₂=k* l _расш;

l _расп= (P₁v₁- P₂v₂).

Из полученных уравнений определяют скорость и расход в выходном сечении сопла при адиабатном истечении газа:

 

.

 

Пренебрегая величиной W₁ и преобразуя, т.к. при истечении обычно известен перепад давлений, получим:

.

 

Расход газа в выходном сечении канала f₂ в кг/сек равен по уравнению неразрывности:

 

,

где

Подставляя значение U₂, получим после преобразований:

 

 

1.5.2 Критическая скорость и критический перепад давления газа при истечении

 

Анализ уравнений скорости и расхода показывает, что величина W постоянно растет при уменьшении отношения , а величина m растет при уменьшении этого отношения до определенного максимума, при , затем уменьшается. Так как последнее противоречит опыту, экспериментально установлено, что при β=β_к скорость и расход достигают максимальной величины и затем остаются постоянными (рисунок 1.17).

		0 bк 1 b=Р2/Р1

 

Рисунок 1.17

Это объясняется тем, что после достижения давления Р ₂= Р_к, несмотря на дальнейшее снижение давления Р₂, давление в выходном сечении канала f₂ остается постоянным и равным. Давление Р_к и соответствующие ему другие параметры называется критическими, а рассматриваемое сечение канала f₂ – критическим сечением:

 

.

 

Приравнивая к нулю первую производную расхода газа (d_m =0), находим максимум функции, для которого определяем критическое соотношение β_к.

Из уравнения расхода следует:

 

.

 

Производя дифференцирование, имеем:

.

 

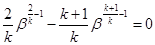Решая полученное уравнение относительно величины β получим:

 

 

Подставляя различные значения k для разных газов, получим:

k= 1,66	βk= 0,49 – для одноатомных газов;
k= 1,4	βk= 0,528 – для двухатомных газов;
k= 1,3	βk= 0,546 – для перегретого пара и трехатомных газов;
k= 1,135	βk= 0,577 – для насыщенного пара.

Подставляя значение β_k в уравнение скорости и расхода, получим значения критической скорости (W_k) и критического (максимального) расхода:

 

 

откуда: ;

 

откуда:

.

Выразим величину критической скорости истечения через параметры состояния в критическом сечении канала Р_k и V_k. из уравнения адиабатного расширения потока газа от давления Р₁ до Р_k имеем:

 

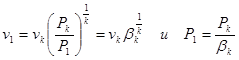
Подставляя полученные значения в уравнение критической скорости истечения, получим:

 

откуда: .

 

Из курса физики известно, что эта скорость равна скорости звука в газе при данных параметрах (Р_k и V_k).

Изложенное позволяет дать физическое объяснение невозможности получения сверхзвуковой скорости истечения из суживающегося канала. Так как импульс давления в сжимаемой среде распространяется со скоростью звука, то при снижении внешнего давления до Р₂ < Р_k, давление в выходном сечении канала будет оставаться равным Р_k, вследствие невозможности распространения импульса снижения давления в потоке, движущемся со звуковой скоростью.

 

1.5.3 Расчет истечения водяного пара

 

Процессы истечения водяного пара рассчитываются с помощью таблиц и диаграмм состояния водяного пара с использованием параметра по формулам, полученным из уравнения первого закона термодинамики:

 

 

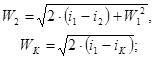
где значение - в Дж/кг определяется из диаграмм и таблиц.

Так как для водяного пара заранее неизвестно из-за неизвестности величины при , расчет ведется методом приближения в следующем порядке.

Задается К=1,135÷1,3 и определяется величина:

 

 

Затем определяется 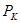из таблиц или диаграмм (при ), определяется и находится новое значение по уравнению адиабаты:

 

 

Расход при истечении водяного пара определяется из формулы неразрывности потока:

 

1.5.4 Расчет комбинированных сверхзвуковых сопел

 

Так как в суживающемся сопле не может быть достигнута скорость истечения больше критической (или звуковой), для получения скорости истечения больше критической (сверхзвуковой) необходимо рассмотреть закономерности изменения формы сечения канала при изменении перепада давления () и скорости истечения ().

Представим уравнение неразрывности в логарифмической форме и продифференцируем его.

Из при имеем , откуда после дифференцирования получим:

 

.

Из уравнения адиабаты после логарифмирования имеем ,

откуда после дифференцирования получим:

 

и .

 

Из уравнения I-го закона термодинамики для адиабатного потока газа:

 

имеем ,

 

т. к. при , то

.

 

Разделив обе части уравнения на , получим:

 

.

 

Подставляя полученные выражения 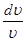и в продифференцированное уравнение неразрывности, получим:

,

 

откуда после преобразований получим:

 

.

 

Анализ полученного выражения для процессов истечения в каналах при и позволяет сделать следующие выводы.

При или и 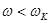, , 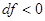т. е. скорость истечения меньше критической скорости истечения и, соответственно, и , то площадь сечения канала должна постоянно уменьшаться (суживающийся канал-сопло).

При или и , , 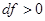т. е. если скорость истечения больше критической скорости истечения и, соответственно, и , то площадь сечения канала должна постоянно увеличиваться (расширяющаяся часть канала-сопла).

Из изложенного следует, что для достижения сверхкритической скорости истечения канал-сопло должен иметь комбинированную форму. Начальный короткий участок сопла, где скорость не достигает критической, должен иметь суживающуюся форму, а после достижения критической скорости сопло переходит в длинный расширяющийся конический участок. Такое комбинированное сопло называется соплом Лаваля (рисунок 1.18).

При этом в узком сечении скорость потока остается равной критической , а давление - 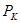. В расширяющейся части происходит дальнейшее падение давления до и увеличение скорости газа до . Выходная скорость течения газа определяется в зависимости от полного перепада давлений по формуле для .

 

 

Рисунок 1.18

 

Максимальный расход газа через такое сопло определяется расходом через узкое (критическое) сечение

,

а выходное сечение комбинированного сопла по величине этого максимального расхода из уравнения неразрывности потока:

 

.

 

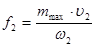Длина конического участка комбинированного сопла определяется из условия, что угол конусности не должен быть больше 8-10°, исходя из изменения диаметра сопла от в горловине до в выходном сечении сопла.

 

1.5.5 Дросселирование газов и паров

 

Дросселированием называется необратимый процесс уменьшения давления газа при прохождении его через сопротивление в канале течения (вентиль, шайба с малым отверстием и др.), происходящий без совершения внешней (полезной) работы.

Дросселирование является неизбежным результатом влияния различных сопротивлений при движении газа в каналах, а также применяется сознательно для определенных целей (регулирование и измерение расхода, редуцирование давления газа или пара и др.).

При дросселировании (рисунок 1.19) скорость потока газа в начале увеличивается в месте сопротивления и затем уменьшается до первоначальной величины, а кинетическая энергия потока вновь превращается в теплоту. Применяя уравнение первого закона термодинамики для потока газа к случаю дросселирования, имеем при :

 

i₂ при

.

 

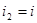Таким образом, при дросселировании теплосодержание не меняется, т.е. дросселирование – изоэнтальпийный процесс. При этом, если известно конечное давление , состояние после дросселирования всегда можно определить по двум параметрам и .

Линия процесса дросселирования пара в -диаграмме – прямая, параллельная оси .

 

Рисунок 1.19

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: