Реальный цикл паросиловой установки – цикл Ренкина

Ввиду низкой практической эффективности идеального цикла паросиловой установки в промышленной теплоэнергетике широко используется реальный цикл паросиловой установки, предложенный Ренкиным.

Для устранения недостатков идеального цикла в цикле Ренкина используются следующие технологические приемы:

– перегрев пара при постоянном давлении Р₁ с целью увеличения средней температуры подвода тепла и осуществления процесса адиабатного расширения, в основном, в области перегретого (сухо­го) пара, что предотвращает потери, связанные с расширением двухфазной смеси;

– полная конденсация пара в процессе отвода тепла с целью замены процесса сжатия двухфазной смеси сжатием жидкости в насосе от давления Р₂ до давления Р₁, что требует значи­тельно меньшего расхода работы и осуществляется с гораздо мень­шими потерями.

На рисунке 1.29 приведена принципиальная схема паросиловой установки, работающей по циклу Ренкина, и дан вид цикла в T – s – диаграмме.

Вода поступает в парогенератор (ПГ), где при постоянном давлении сначала нагревается до температуры кипения (процесс 4–5), а затем испа­ряется, превращаясь в сухой насыщенный пар (процесс 5–6).

Насы­щенный водяной пар перегревается в пароперегревателе (ПП) (процесс (6–1). С давлением P₁ и температурой T₁ он поступает в паровую турбину (ПТ), где в процессе адиабатического расширения от давления P₁до давления P₂(процесс 1–2) совер­шает полезную работу, которая преобразуется в электрическую энер­гию в электрогенераторе (ЭГ).

 

 

 

 

Рисунок 1.29 – Схема и цикл паросиловой установки Ренкина

 

Отработанный пар с давлением Р₂ поступает в конденсатор, где охлаждается и конденсируется при P₂ =const (процесс 2–3). Давление конденсата P₂ поднимается до давления котловой воды P₁ питательным насосом (ПН) (процесс 3–4), после чего она подается в парогенератор (ПГ).

Для нагревания и испарения воды и перегрева пара в парогенератор подводится тепло q₁, которое получается за счет сжигания органического топлива или в результате тепловыделения от ядерных реакций расщепления тяжелых трансурановых элементов в атомном реакторе.

Конденсатор охлаждается водой, которая отводит в окружающую среду тепло q₂. В турбине совершается полезная работа, которая на рабочем валу электрогенератора превращается в электрическую энергию. Для привода питательного насоса затрачивается энергия L_H, подводимая извне.

Термический к.п.д. цикла Ренкина определяют из выражения:

 

где

 

Так как процессы подвода и отвода тепла происходят при Р = const, то:

L_T = i₁ – i₂ –располагаемая работа потока пара в турбине;

L_H = i₄ – i₃ – работа,расходуемая на привод насоса.

Если пренебречь работой L_H и принять i₄ ~= i₃, то приближенно к.п.д. цикла Ренкина будет равен:

 

.

 

Удельный расход пара выработку единицы энергии (10³ кДж) составит:

 

.

 

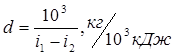Пути повышения экономичности цикловпаросиловых установок

 

Влияние параметров на к.п.д. цикла Ренкина.

I. Увеличение начального давления и температуры пара перед турбиной приводит к увеличению средней температуры подвода тепла и увеличивает полезный теплоперепад (i₁ – i₂) в турбине. Все это увеличивает к.п.д. цикла.

Пределы увеличения этих параметров (P₁ и t₁) в настоящее время ограничены величиной давления 220 бар и темпера­туры 560 - 570 °С по условиям прочности металла труб парогенератора и пароперегревателя.

2. Уменьшение конечного давления пара после турбины увеличивает теплоперепад (i₁ – i₂) и к.п.д. цикла в целом. Предельное значение давления P₂ - 0,03 - 0,04 кПа, что свя­зано с условиями охлаждения, с температурой и расходом охлаждаю­щей воды.

3. Применение вторичного перегрева пара. Применение высоких начальных параметров пара, особенно уве­личение давления, сдвигает конечную точку процесса расширения па­ра в турбине (i₁ – i₂), в область высокой влажности пара (величина X₂ при этом уменьшается).

Повышение влажности пара при расширении вредно действует на последние ступени турбины (эрозионный износ, снижение к.п.д. турбины и т. д.) и ограничивается величиной 13 –14 % (X₂ = 0,86 - 87).

Применение вторичного перегрева пара позволяет уменьшить влажность в конце процесса расширения (рисунок 1.30).

 

 

 

Рисунок 1.30

При этом перегретый пар из парогенератора, поступивший на турбину с параметрами P₁ и t₁, расширяется адиабатичес­ки до промежуточного давления, P₂, процесс (1-2), после чего направляется в промежуточный (или вторичный) пароперегреватель, где повторно перегревается до температуры t₃, процесс (2-3) при давлении P₂ и возвращается в турбину. В турбине этот пар расширяется до конечного давления P₄ и идет в конденсатор.

Конечная влажность после расширения здесь уменьшается (X₄>X₄). К.П.Д. цикла Ренкина с вторичным перег­ревом равен:

 

 

При этом если средняя темпе­ратура подвода тепла при вторичном перегреве пара (T_{cp в.n}) будет выше, чем в основной части цикла, то общий к.п.д. цикла Ренки­на увеличится, что даст дополнительно и экономический эффект.

4. К.п.д. цикла Ренкина невысок и при самых лучших условиях равен 0,4 - 0,45 для теоретического цикла, а с учетом потерь в реальных установках равен 0,3 - 0,35. Основная потеря в цикле это q₂, т. к. давление отработанного пара турбин Р₂= 0,03-0,04 ата и температура его t₂ (25 – 30 °С) очень малы, что делает невозможным полезное использование тепла этого пара после тур­бины.

Если увеличить давление Р₂ до 1,5-10 ата, то к.п.д. паросиловой установки снизится, но отработанный пар может быть полезно использован для производственных и бытовых нужд (рисунок 1.31).

Эффективность цикла при этом оценивается по комплексному итогу использования тепла под­водимого в парогенераторе и определяется коэффициентом теплоиспользования:

 

 

Для реальных установок К_Т.И = 0,8-0,85. Комбинированная выработка на одной теплосиловой установке электрической энергии и тепло­вой энергии для бытовых и производственных нужд называется тепло­фикацией, а теплосиловые установки, в которых осуществляется та­кая комбинированная выработка тепловой и электрической энергии называются теплоэлектроцентралями (ТЭЦ).

 

 

Рисунок 1.31

1.6.7 Термодинамические основы получения искусственного холода

 

а) Цикл газовой холодильной машины

Применение цикла Карно затрудняется сложностью осуществления изотермического подвода и отвода тепла.

В реальных аппаратах теплообмен происходит при постоянном давлении движущихся сред, разделенных поверхностью теплообмена. Поэтому, цикл газовой холодильной машины состоит из двух адиабат и двух изобар. В качестве холодильного агента в этих машинах используют газ (воздух, углекислота, инертные газы и др.).

Схема и цикл газовой холодильной машины диаграмме Т-S приведены на рисунке 1.32.

 

Рисунок 1.32

Последовательность процессов в цикле газовой холодильной машины:

1-2 – адиабатное сжатие в компрессоре (КМ) от давления Р₁ до Р₂, затрачивается работа l_к;

2-3 – изобарное охлаждение сжатого газа в теплообменнике охладителя конденсата (ТО ОК) при Р₂=сonst с отводом тепла q₁ в окружающую среду;

3-4 – адиабатное расширение газа в детандере (ДТ) от Р₂ до Р₁ с совершением полезной работы l_д;

4-1 – изобарный подогрев газа в теплообменнике (ТО ХК) с отводом тепла q₂ из холодильной камеры (ХК).

Затраченная работа равна l=l_к-l_д=q₁-q₂, где q₂-холодопроизводительность.

Холодильный коэффициент газовой холодильной машины равен:

 

e_г= .

 

Если принять q₁=Т_1ср·DS и q₂=Т_2ср·DS, то:

 

e_г= .

 

Так как всегда Т_1ср> Т_окр= Т₁ и Т_2ср<Т_хол =Т₂, то:

 

e_г= < ,

 

где e_к – холодильный коэффициент обратного цикла Карно 1-2’-3-4’-1, осуществленного при том же перепаде температур Т_окр и Т_хол, что и цикл газовой холодильной машины;

Т_1ср, Т_2ср – условная среднеинтегральная температура отвода и подвода тепла в цикле газовой холодильной машины.

Газовые холодильные машины, использующие воздух в качестве рабочего тела, были первыми промышленными холодильными установками. В настоящее время в промышленности они вытеснены парокомпрессорными холодильными машинами и применяются только для целей глубокого охлаждения.

Преимуществом газовых холодильных машин является простота устройства, очень низкая стоимость холодильного агента, безопасность работы и др.

Недостатки газовых холодильных машин состоят в низкой экономичности, вследствие чего они были вытеснены парокомпрессорными холодильными машинами.

 

б) Идеальный цикл парокомпрессорной холодильной машины

Если в качестве холодильного агента использовать пары веществ, кипящих при низких температурах, то возможно осуществление обратного цикла с теплообменом при постоянной температуре и при постоянном давлении одновременно, так как при испарении жидкости (подвод тепла) и при конденсации паров (отвод тепла) температура и давление холодильного агента остаются постоянными.

Обратный цикл, осуществленный в области влажного пара, будет полностью аналогичным циклу Карно и называется идеальным циклом парокомпрессорной холодильной машины (ПКХМ) (рисунок 1.33).

Схема машины аналогична схеме газовой холодильной машины. Рабочим телом в ней являются пары низкокипящих веществ (аммиак, фреон и др.)

Для парокомпрессорной холодильной машины приняты следующие условные обозначения:

 

 

Р_к, q_к и Т_к – давление, тепло и температура конденсации паров холодильного агента в процессе отвода тепла;

Р_о, q_о и Т_о – давление, тепло и температура испарения жидкого холодильного агента в процессе подвода тепла.

Величина q_о является так же холодопроизводительностью ПКХМ.

Так как в процессах 4-1 и 2-3 давление постоянно, то q_2-3 =i₂-i₁ = =q₁ = q_к, а q_4-1=i₁-i₄=q₂=q_о.

Кроме того, для компрессора и детандера справедливо равенство l_к=i₂--i₁ и l_д=i ₃-i ₄, а работа затраченная в цикле l=l_к-l_д.

Холодильный коэффициент идеального цикла ПКХМ равен холодильному коэффициенту цикла Карно, откуда:

 

e_п=

e_п= .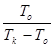

 

Подставляя значение количества тепла имеем:

 

e_п= .

 

 

в) Расчет рабочего режима холодильной установки

Рабочий режим холодильной установки характеризуется температурами кипения t_о, конденсации t_к, переохлаждения (жидкого хладагента перед регулирующим вентилем) t_п, всасывания (пара на входе в компрессор) t_вс.

Температуру кипения хладагента принимают в зависимости от температуры воздуха в охлажденном объекте. При непосредственном охлаждении температура кипения обычно на 7¸10 °С ниже температуры воздуха в камере:

 

t_о = t_в – (7¸10). °С

 

В рассольных схемах температуру кипения хладагента принимают на 5¸6 °С ниже температуры рассола, которую в свою очередь принимают на 8¸10 °С ниже температуры воздуха в камере, т. е.:

 

t_р1 = t_в – (8¸10); °С

t_о = t_р – (5¸6). °С

 

Остальные температуры выбираются так же, как и для системы непосредственного охлаждения.

Температура воды на входе в конденсатор зависит от внешних условий:

 

t_вд1 = t_н - (4¸6), ° С

 

где t_н – средняя летняя температура наружного воздуха,°С.

Нагрев воды в конденсаторе принимается до 5°С, тогда:

 

t_вд2 = t_вд1 + 5.°С

 

Температуру конденсации принимают на 3¸5 °С выше температуры воды, отходящей от конденсатора:

 

t_к = t_вд2 + (3¸5). °С

 

Выбор разности температур в конденсаторе должен быть экономически обоснован, чтобы затраты были минимальными, поэтому для машин, работающих на хладонах, средние разности температур между хладагентом и водой примерно вдвое больше, чем для машин, работающих на аммиаке.

Температура переохлаждения хладагента перед регулирующим вентилем выше температуры подаваемой в переохладитель воды на 3¸5°С:

 

t_по = t_вд1 + (3¸5). °С

 

Свежая вода подается на переохладитель, а затем добавляется к оборотной воде, поступающей в конденсатор.

Для исключения влажного хода компрессора пар перед компрессором перегревается. Безопасность работы обеспечивается при перегреве пара:

– для аммиака t_вс = t_о + (5¸15)°С;

– для хладонов t_вс = t_о + (20¸30)°С,

при этом верхний предел относится к хладону -12, а нижний – к хладону-22.

Построение процесса в i-lgP диаграмме (рисунок 1.34) проводится на основании принятых значений температур в характерных точках цикла в следующей последовательности:

 

 

 

Рисунок 1.34 – Построение цикла ПКХМ в i-lgP диаграмме

1. На i-lgP диаграмму наносят изотермы, определяющие режим работы установки - t_о, t_к, t_по, t_вс.

2. По температурам t_о и t_к находят соответствующие изобары Р_о и Р_к в области перегретого пара и переохлажденной жидкости.

3. В результате построения на диаграмме получены опорные точки:

1’– на пересечении изотермы t_о с линией сухого насыщенного пара;

2’ – на пересечении изотермы t_к с линией сухого насыщенного пара;

3’ – на пересечении изотермы t_к с линией жидкости;

3 – на пересечении изотермы t_по с изобарой Р_к в области переохлажденной жидкости.

4. На пересечении линий t_вс и Р_о в области перегретого пара находят точку 1, определяющую состояние пара, всасываемого компрессором.

5. Через точку 1 проводят линию постоянной энтропии (адиабату) до пересечения с изобарой Р_к в точке 2, которая определяет состояние пара в конце сжатия.

6. Точка 4 находится на пересечении линии постоянной энтальпии, проходящей через точку 3, с изотермой t_о и изобарой Р_о в области влажного пара. Точка 4 характеризует состояние хладагента после дросселирования в регулирующем вентиле.

Процессы, изображенные в диаграмме:

4-1’ – кипение в испарителе при t_о и Р_о. Принято, что из испарителя выходит сухой насыщенный пар;

1’-1 – перегрев пара на всасывании от t_о до t_вс при постоянном давлении Р_о;

1-2 – адиабатное сжатие в компрессоре;

2-3’ – процесс отвода тепла в конденсаторе, который можно разделить на два процесса:

2-2’ – охлаждение пара до состояния насыщения (сбив перегрева) при постоянном давлении Р_к;

2’- 3’ – конденсация хладагента при t_к и Р_к;

3’- 3 – переохлаждение жидкого хладагента в конденсаторе, переохладителе или теплообменнике от t_к до t_по при давлении Р_к;

3 - 4 – дросселирование хладагента в регулирующем вентиле от Р_к до Р_о по линии постоянной энтальпии.

По таблицам насыщенных паров, в зависимости от типа хладагента определяют параметры точек, находящихся на пограничных кривых (для сухого насыщенного пара и для насыщенной жидкости) и в области переохлажденной жидкости:

1’– при t_о для сухого насыщенного пара;

2’ – при t_к для сухого насыщенного пара;

3’ – для жидкости при t_к;

3 – для жидкости по t_по.

Параметры точек 1, 2 и 4 определяют по диаграмме согласно построению:

1- в области перегретого пара на пересечении линий Р_о и t_вс;

2- в области влажного пара на пересечении линий S₁=соnst и Р_к;

4- в области влажного пара на пересечении линий i₃=сonst и t_о, Р_о.

 

 

2- Введение

Процесс передачи тепла является важным условием осуществления любого термодинами­ческого цикла, т. к. в соответствии со 2-м законом термодинамики, любой термодинамический цикл должен иметь процессы подвода и отвода тепловой энергии. Многие технологические процессы также включают теплообмен, например процессы подогрева и охлаждения продукта, процессы сушки, выпарки и т. д. Теплообмен многократно осуществляется в системах промышленного и коммунально-бытового теплоснабжения, в системах отопления, вентиляции и горячего водоснабжения. Из изложенного следует, что теория теплообмена имеет большое практическое значение для правильного применения процессов получения, использования и преобразования тепловой энергии.

Перенос тепла от одного тела к другому происходит под воздействием разности температур, от большей температуры к меньшей, и может быть осуществлен тремя способами.

1. Теплопроводность

Теплопроводностью называется процесс распространения тепла путем непосредственного соприкосновения частиц тела (молекул, атомов, электронов), неподвижных относительно друг друга. Таким путем тепло передается в твердых телах или неподвижных тонких слоях жидкости или газа.

Из определения видно, что теплопроводность является процессом малой интенсивности. Скорость передачи тепловой энергии при теплопроводности невелика и зависит от разности температур между соседними частицами, обменивающимися энергией, т. е. от интенсивности изменения температуры в направлении распространения тепловой энергии.

2. Конвекция

Конвекцией называется перенос тепла в пространстве движущимися частицами жидкости, газа или твердых тел. Конвекция бывает свободной (естественной) и вынужденной. Конвекция всегда сопровождается теплопроводностью. На заключительном этапе, когда движущиеся частицы жидкости или газа передают тепловую энергию неподвижным частицам твердого тела при непосредственном соприкосновении. Такой комбинированный процесс переноса тепла, включающий конвекцию в жидкости и теплопроводность на границе между жидкостью и твердой стенкой, называется конвективным теплообменом или теплоотдачей. Теплоотдача является основным видом переноса тепловой энергии от жидкости или газа к твердой поверхности и обратно.

Конвекция является процессом переноса тепловой энергии большей интенсивности, скорость которого зависит от скорости движения частиц жидкости или газа в пространстве, т. е. при вынужденной конвекции эта скорость практически ничем не ограничена.

Интенсивность процесса конвективного теплообмена ограничивается процессом теплопроводности на границе жидкости с твердой поверхностью и в пограничном слое относительно неподвижных частиц жидкости, прилегающем к твердой поверхности. Интенсивность конвективного теплообмена может быть увеличена при увеличении скорости движения жидкости относительно твердой поверхности, что способствует уменьшению толщины пограничного слоя.

3. Тепловое излучение

Тепловым излучением называется процесс переноса тепла в пространстве в форме энергии (электромагнитных колебаний) без непосредственного соприкосновения тел. Лучистая энергия, испускаемая одним телом, проходит сквозь прозрачную среду, поглощается другим телом, превращаясь в тепло. При переносе тепла за счет теплового излучения происходит двойное преобразование энергии.

На первом этапе тепловая энергия на поверхности первого тела в результате сложных внутриатомных процессов (переход электронов на более низкий энергетический уровень и т. д.) частично преобразуется в энергию электромагнитных колебаний, которая излучается с поверхности первого тела в пространство и распространяется в нем со скоростью света. На втором этапе энергия электромагнитных колебаний (энергия излучения) попадает на поверхность другого тела и вновь преобразуется в тепловую энергию.

Интенсивность теплового излучения определяется количеством излучаемой энергии с поверхности тела, которое, в свою очередь, увеличивается с увеличением температуры тела. Поэтому процесс теплового излучения наиболее эффективно может быть использован при высоких температурах тел (топки котлов, печей и др.).

На практике, когда разные виды переноса тепла встречаются одновременно, такие процессы переноса тепла называются сложным теплообменом.

В зависимости от характеристики течения процессы теплообмена происходят при установившемся (стационарном) режиме, когда температуры во всех точках постоянные во времени и неустановившемся (нестационарном) режиме.

Теплообмен обычно рассматривают при установившемся режиме, за исключением процессов нагревания и охлаждения тел.

 

Теплопроводность

 

2.1.1 Основные определения

 

Процесс распространения тепловой энергии (теплопроводность) в твердом теле есть функция изменения температуры внутри этого тела.

В свою очередь, температура в любой точке тела при установившемся режиме есть функция координат этой точки .

Температурным полем называется совокупность всех значений температур во всех точках рассматриваемого тела.

Изотермической поверхностью называется поверхность, соединяющая в пространстве две точки с одинаковой температурой. Изотермические поверхности не пересекаются между собой, не имеют разрывов и скачков и в общем случае имеют произвольную форму.

Температурное поле в общем случае трехмерное.

В простейшем случае температурное поле одномерное, то есть температура изменяется в направлении одной оси; изотермические поверхности есть плоскости, перпендикулярные оси; температурный градиент направлен вдоль оси, температурный градиент направлен вдоль оси в положительную сторону.

Распространение тепла идет всегда в сторону убывания температуры.

Характеристиками температурного поля в любой его точке являются две величины:

– градиент температуры , характеризующий интенсивность изменения температуры по расстоянию;

– удельный тепловой поток , характеризующий интенсивность переноса тепловой энергии по направлению.

Температурным градиентом называется вектор, показывающий интенсивность изменения температуры в направлении нормали к изотермической поверхности в данной точке А, равный:

 

, (2.1)

 

где – изменение температуры;

– соответствующее этому температурному перепаду изменение расстояния.

Этот вектор направлен в сторону увеличения температуры.

Расчетная схема температурного поля к определению градиента температуры представлена на рисунке 2.1.

 

Рисунок 2.1 – Расчетная схема градиента температурного поля

 

Удельным тепловым потоком или поверхностной плотностью теплового потока называется вектор, определяющий количество тепловой энергии, проходящей в единицу времени через единицу площади изотермической поверхности в направлении нормали в данной точке. В общем случае величина удельного теплового потока будет равна:

 

 

Этот вектор направлен в сторону понижения температуры.

 

1.1.2 Основной закон теплопроводности – закон Фурье

Закон Фурье устанавливает связь между характеристиками температурного поля в любой его точке.

Удельный тепловой поток при теплопроводности пропорционален градиенту температуры и направлен в обратную сторону по отношению к градиенту температуры. Математическое выражение закона Фурье имеет вид:

 

. (2.2)

 

Знак (–) учитывает, что вектор теплового потока направлен противоположно вектору градиента температур.

Коэффициент пропорциональности называется коэффициентом теплопроводности (Вт/м×град) и является важной характеристикой способности тел передавать или задерживать тепло при теплопроводности. = 400 – 500 Вт/м×град для металлов (медь – сталь), применяемых в теплообменниках, = 0,2 ¸ 0,05 Вт/м×град – для теплоизоляционных материалов.

Уравнение Фурье дает математическое описание произвольного температурного поля в дифференциальной форме.

Для получения расчетных зависимостей процесса теплопроводности в конкретных условиях необходимо дифференциальное уравнение Фурье дополнить математическим описанием всех частных особенностей конкретного процесса.

Таковыми особенностями являются условия однозначности (размеры, форма, физические характеристики тела, температурные условия и т. д.) и краевые условия (начальные и граничные условия).

В качестве примера рассматривается решение задачи теплопроводности для наиболее простых, но практически важных случаев – теплопроводность плоской и цилиндрической стенки в стационарных условиях.

2.1.3 Теплопроводность плоских стенок

 

а)Теплопроводность в однослойной плоской стенке

 

Рассмотрим однородную плоскую стенку с толщиной , м и коэффициентом теплопроводности материала стенки , представленную на рисунке 2.2.

Температурное поле в плоской стенке одномерное, а его градиент направлен по нормали к стенке, совпадающей с осью Х. Изотермические поверхности в этом температурном поле представляют собой плоскости, параллельные наружным поверхностям стенки. Температура на левой поверхности стенки во всех точках равна t_ст1, на правой – t_ст2 . Поток тепла направлен от t_ст1 к t_ст2, и его величина постоянна для всей стенки, так как площадь всех изотермических поверхностей одинаковая.

 

 

Рисунок 2.2 – Схема температурного поля однослойной плоской стенки

 

Установим начало координат на левой поверхности стенки и выделим на расстоянии две изотермические поверхности на расстоянии друг от друга при изменении температуры на .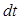

Уравнение теплопроводности (закон Фурье) для слоя будет иметь вид:

.

 

Разделяя переменные, получим:

 

.

Интегрируя полученное дифференциальное уравнение, будем иметь:

 

.

 

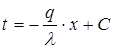Из полученного уравнения следует, что, при температура в плоской стенке изменяется по линейному закону (рисунок 2.2).

Постоянная интегрирования находится из граничных условий:

– при Х = 0 t = t_ст1;

– при Х = t = t_ст2.

Подставляя первое граничное условие, имеем:

 

С = t_ст1 и .

 

Подставляя второе граничное условие, получим уравнение вида:

 

.

 

Решая полученное уравнение относительно величины , получим зависимость для определения теплового потока в плоской стенке:

 

. (2.3)

 

Обозначим величину , К·м²/Вт и назовем ее термическим сопротивлением плоской стенки, тогда уравнение теплового потока для плоской стенки примет вид:

 

. (2.4)

 

Уравнение теплопроводности в таком виде аналогично закону Ома для проводника, где тепловой поток соответствует силе тока, – разности потенциалов – движущей силе процесса, а R – электрическому сопротивлению.

Строительные и теплоизоляционные материалы имеют низкий коэффициент теплопроводности, зависящий от температуры материала. Обычно эту зависимость представляют в следующем виде:

 

. (2.5)

 

В этом случае уравнение теплопроводности будет иметь вид:

 

.

 

Разделяя переменные, получим выражение:

 

,

 

что после интегрирования дает:

 

.

 

Определяем постоянную интегрирования из принятых граничных условий. После подстановки приходим к выражениям вида:

 

;

 

;

.

 

Если представить величину , то приходим к выражению:

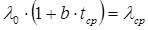, и . (2.6)

 

б) Теплопроводность в многослойной плоской стенке

 

На практике плоская стенка встречается наиболее часто в виде многослойной конструкции с параллельными плотно прилегающими слоями.

Рассмотрим многослойную плоскую стенку, состоящую из однородных параллельных слоев с толщиной и коэффициентом теплопроводности в каждом слое. Температура на наружной поверхности первого слоя во всех точках равна , на поверхности последнего слоя – . Тепловой поток – постоянная величина для всех слоев и направлен в сторону понижения температуры.

Схема температурного поля такой многослойной плоской стенки представлена на рисунке 2.3.

 

 

Рисунок 2.3 – Схема температурного поля многослойной плоской стенки

 

Запишем уравнения теплопроводности для каждого слоя в отдельности и представим их в виде системы:

 

 

Решая полученные уравнения относительно разности температур и складывая почленно их левые и правые части, после сокращения одинаковых температур с разными знаками, будем иметь:

 

 

Тогда уравнение теплового потока можно представить в виде:

 

Обозначим выражение в знаменателе как – термическое сопротивление многослойной стенки. Тогда уравнение теплового потока окончательно примет вид:

 

(2.7)

 

По аналогии с последовательным соединением электрических проводников, термическое сопротивление многослойной стенки равно сумме термических сопротивлений всех ее отдельных слоев.

Для определения температуры в любом промежуточном слое t_i+1 используем условие постоянства теплового потока при любом числе слоев:

 

,

 

откуда получаем выражение:

 

(2.8)

 

2.1.4 Теплопроводность цилиндрических стенок

 

а) Теплопроводность в однослойной цилиндрической стенке

 

Рассмотрим однородную однослойную цилиндрическую стенку, коэффициент теплопроводности материала которой l, радиусы внутренней и внешней поверхности r₁ и r₂, а температуры в каждой точке этих поверхностей соответственно равны t₁ и t₂. Схема температурного поля однослойной цилиндрической стенки представлена на рисунке 2.4.

Температурное поле в такой стенке двухмерное, а изотермические поверхности представляют собой цилиндры, соосные с внутренней и наружной поверхностью. Удельный тепловой поток q направлен от t₁ до t₂ и является переменной величиной, так как площадь изотермической поверхности увеличивается с ростом радиуса r.

Полный тепловой поток через стенку есть величина постоянная для всех сечений при стационарном режиме:

 

Q = q×F= const. (2.9)

 

 

 

 

Рисунок 2.4 – Схема температурного поля однослойной цилиндрической стенки

 

Для анализа теплопроводности в цилиндрической стенке выделим внутри стенки на радиусе r от центральной оси две изотермические поверхности на расстоянии dr друг от друга при изменении температуры между ними на dt.

Уравнение Фурье для элементарного слоя цилиндрической стенки толщиной dr будет иметь вид:

.

 

Так как величина q зависит от r, то для решения полученного дифференциального уравнения необходимо установить вид этой зависимости.

Из условия Q = const имеем:

,

 

где l – длина цилиндрической ст

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: