 |
Ставка процента, учитывающая инфляцию. Формула Фишера.
|
|
|
|
ИНВЕСТИЦИИ
Учебное пособие
Санкт-Петербург
ББК У263я7
Печатается по решению
Редакционно-издательского совета СЗАГС
Клоков В. И. Инвестиции: Учебное пособие. – СПб.: Изд-во СЗАГС, 2009. –
212 с.
Рецензенты:
доктор технических наук, профессор, заслуженный деятель науки и техники РФ В. А. Курзенев;
кандидат экономических наук, профессор А. К. Нещерет.
Учебное пособие рассматривает количественные методы оценки эффективности инвестиций. Приведены показатели эффективности инвестиционных проектов, оценки доходности и риска портфеля ценных бумаг. Описаны методы построения оптимального портфеля ценных бумаг, разработанные Г. Марковицем,
Д. Тобиным и У. Д. Шарпом. Имеются многочисленные примеры экономических расчетов, в том числе и в Excel.
Пособие предназначено для студентов (бакалавров, магистров) и аспирантов, специализирующихся в экономике, моделировании социальных и экономических процессов, а также для всех желающих повысить свою финансовую грамотность.
© СЗАГС, 2009
© Клоков В. И.
ISBN 978-5-89781-348-3
СОДЕРЖАНИЕ
РАЗДЕЛ I. ВЫПИСКА ИЗ ОРАЗОВАТЕЛЬНОГО СТАНДАРТА……6
РАЗДЕЛ II. ЛЕКЦИИ.. 8
Введение. 8
1. ТОВАРЫ ФИНАНСОВОГО РЫНКА.. 11
2. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ.. 17
2.1. Основные понятия. 18
2.2. Кредитование. 20
2.3. Дисконтирование. 35
2.4. Эффективная ставка. 40
2.5. Непрерывная ставка (сила роста) и непрерывный дисконт. 45
3. ПОТОКИ ПЛАТЕЖЕЙ.. 53
3.1. Однонаправленные потоки платежей. 53
3.2. Финансовая рента (аннуитет) 56
3.3. Двусторонние потоки платежей. Эффективная ставка операции. 71
3.4. Эффективная ставка кредита. 76
3.5. Финансовые вычисления по ценным бумагам.. 81
3.6. Вероятностные характеристики платежей. 90
|
|
|
4. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА.. 103
4.1 Критерии оценки эффективности инвестиционного проекта. 103
4.2. Чистое современное значение NPV (net present value) 104
4.3. Эффективная ставка, внутренняя эффективность, внутренняя норма доходности (internal rate of return, IRR) 106
4.4. Срок (время) окупаемости инвестиционного проекта (discount payback period, DPP) 108
4.5. Норма рентабельности, индекс доходности инвестиционного проекта (profitability index, pi) 111
5. МОДЕЛИРОВАНИЕ РИСКОВ НА РЫНКЕ ЦЕННЫХ БУМАГ. 118
5.1. Финансовый риск. 118
5.2. Неравенство Чебышева. 119
5.3. Хеджирование. 121
6. ПОРТФЕЛЬ ЦЕННЫХ БУМАГ. 123
6.1. Характеристики портфеля ценных бумаг. 123
6.2. Оценка доходности и риска портфеля ценных бумаг. 130
6.3. Портфель из независимых ценных бумаг. Диверсификация портфеля 132
6.4. Портфель из коррелированных ценных бумаг. 133
6.5. Портфель из антикоррелированных ценных бумаг. 133
7. ОПТИМАЛЬНЫЙ ПОРТФЕЛЬ ПРИ РИСКОВАННЫХ ВЛОЖЕНИЯХ (H. MARKOWITZ)…………………………………..135
8. ОПТИМАЛЬНЫЙ ПОРТФЕЛЬ ЦЕННЫХ БУМАГПРИ БЕЗРИСКОВЫХ И РИСКОВАННЫХ ВЛОЖЕНИЯХ (J. TOBIN)..148
9. СТАТИСТИКА ФОНДОВОГО РЫНКА.. 170
ЗАКЛЮЧЕНИЕ.. 174
ПРИЛОЖЕНИЕ.. 175
РАЗДЕЛ Ш. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ... 186
РАЗДЕЛ IV. ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.. 189
Занятие № 1. Тема «финансовые вычисления». 189
1.1. Основные понятия. 189
1.2. Кредитование. 189
1.3. Дисконтирование. 191
1.4. Эффективная ставка. 191
1.5. Непрерывная ставка (сила роста) и непрерывный дисконт. 192
Занятие № 2. Тема «потоки платежей». 193
2.1. Однонаправленные потоки платежей. 193
2.2. Финансовая рента (аннуитет) 193
2.3. Двусторонние потоки платежей. 193
2.4. Эффективная ставка операции. 194
Занятие № 3. Тема «Финансовые вычисления по ценным бумагам». 195
Занятие № 4. Тема «Оценка эффективности инвестиционного проекта». 196
Занятие № 5. Тема «Финансовый риск». 197
Занятие № 6. Тема «Портфель ценных бумаг». «Построение оптимального портфеля ценных бумаг при рискованных вложениях». 198
|
|
|
РАЗДЕЛ V. СЛОВАРЬ ОСНОВНЫХ ПОНЯТИЙ.. 200
РАЗДЕЛ VI. ПРИМЕРНЫЕ ТЕМЫ КУРСОВЫХ РАБОТ.. 207
РАЗДЕЛ VII. ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ВОПРОСОВ К ИТОГОВОЙ АТТЕСТАЦИИ 209
РАЗДЕЛ I.
ВЫПИСКА ИЗ ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА
Инвестиции
Экономическая сущность и виды инвестиций. Инвестиционный процесс. Финансовые институты. Финансовые рынки. Участники инвестиционного процесса. Типы инвесторов. Экономическая сущность, значение и цели инвестирования. Понятие инвестиционного проекта, содержание, классификация, фазы развития. Критерии и методы оценки инвестиционных проектов. Состоятельность проектов. Критические точки и анализ чувствительности. Бюджетная эффективность и социальные результаты реализации инвестиционных проектов. Инвестиционные качества ценных бумаг. Формы рейтинговой оценки. Доходность и риск в оценке эффективности инвестиций в ценные бумаги. Понятие инвестиционного портфеля. Типы портфеля, принципы и этапы формирования. Доход и риск по портфелю. Модели формирования портфеля инвестиций. Оптимальный портфель. Стратегия управления портфелем. Инвестиции, осуществляемые в форме капитальных вложений: объекты и субъекты, права, обязанности и ответственность. Формы и методы государственного регулирования инвестиционной деятельности, осуществляемой в форме капитальных вложений. Государственные гарантии и защита капитальных вложений. Организация подрядных отношений в строительстве. Источники финансирования капитальных вложений. Собственные, привлеченные и заемные средства. Условия предоставления бюджетных ассигнований. Иностранные инвестиции. Режим функционирования иностранного капитала в России. Бюджетное финансирование, самофинансирование, акционирование. Методы долгового финансирования. Внешние финансовые рынки. Долгосрочное кредитование. Лизинг, виды и преимущества. Проектное финансирование. Венчурное финансирование. Ипотечное кредитование.
Рынок ценных бумаг
Рынок ценных бумаг как альтернативный источник финансирования экономики. Понятие ценной бумаги. История появления ценных бумаг. Классические виды ценных бумаг и их характеристика (акции, частные облигации, государственные ценные бумаги). Производные ценные бумаги и их характеристика (конвертируемые акции и облигации, варранты, опционы и фьючерсы). Финансовые инструменты на рынке ценных бумаг (векселя, депозитные, сберегательные, инвестиционные сертификаты, секъюритизация частных долгов). Международные ценные бумаги (евроноты, еврооблигации, евроакции). Рынок ценных бумаг и его структура (западная модель). Первичный рынок ценных бумаг и его характеристика. Методы размещения ценных бумаг. Участники первичного внебиржевого рынка ценных бумаг. Вторичный биржевой рынок ценных бумаг (фондовая биржа). Организационная структура и функции фондовой бирже. Основные операции и сделки бирже. Биржевая информация (биржевые индексы и их характеристика). Участники вторичного рынка. Брокерские компании (организации, функции, механизм операций). Торговая регистрация, сопоставление и расчетный процесс. Механизмы принятия решений на рынке ценных бумаг (фундаментальный и технический анализ). Эмиссия ценных бумаг. Инвестиционная деятельность кредитно-финансовых институтов на рынке ценных бумаг (западная и российская модели) – банков, страховых компаний, инвестиционных компаний, пенсионных фондов и прочих институтов. Рынок ценных бумаг Российской Федерации.
|
|
|
РАЗДЕЛ II. ЛЕКЦИИ
Введение
Несмотря на то, что в последнее время появилось достаточно много работ, посвященных рыночной экономике, до сих пор учебно-методических пособий, рассматривающих вопросы финансовой математики, в том числе, вопросы построения методов оценки финансовых рисков и способов формирования оптимального портфеля ценных бумаг, явно недостаточно.
Данное пособие составлено на основании курса лекций «Инвестиции» и «Финансовый рынок: расчет и риск», читаемых в СЗАГС.
В работе рассмотрены следующие вопросы.
В главе 1 представлены общие свойства финансового рынка и основные товары финансового рынка: облигации, акции, векселя, государственные финансовые обязательства, опционы, фьючерсы, варранты и т. д.
Глава 2 посвящена финансовым вычислениям: кредитованию, дисконтированию и оценке эффективной ставки. Наряду с дискретными вычислениями приведены методы расчета в непрерывном случае, когда процент кредитования или дисконтирования начисляется непрерывно.
|
|
|
В главе 3 приведены более сложные схемы расчетов финансовых потоков, когда имеются односторонние и двусторонние потоки платежей. Рассмотрены методы расчета для потока платежей эффективной ставки, которая оценивает целесообразность использования данного потока платежей. Подробно изложены способы расчета частного случая потока платежей: аннуента или финансовой ренты, когда выплаты производятся через равные промежутки времени. Приведены основные формулы и примеры их использования для расчетов по ценным бумагам. Рассмотрен вероятностный подход к оценке потоков платежей. Здесь содержатся необходимые для понимания этого раздела сведения из теории вероятности и математической статистики. Этот пункт лежит несколько в стороне от основного содержания пособия и при первом прочтении может быть опущен.
В главе4описаны методы оценки эффективности инвестиционного проекта. Рассмотрены показатели эффективности инвестиций: чистое современное значение NPV, эффективная ставка (внутренняя эффективности) IRR, срок окупаемости Pb, норма (индекс) рентабельности инвестиционного проекта H. Приведены основные расчетные формулы и примеры расчета показателей эффективности инвестиционного проекта с помощью функций Excel. Рассмотрен пример оценки окупаемости инвестиционного проекта.
Основные элементы финансовой математики, приведенной в главах 2, 3 носят универсальный характер и могут быть использованы как для финансовых расчетов по ценным бумагам, так и для финансовых расчетов производственной деятельности.
Последующие разделы посвящены, в основном, описанию процессов, происходящих на фондовом рынке.
В главе5 вводятся понятия финансового риска и хеджирования. Приведен пример использования неравенства Чебышева для оценки вероятности разорения инвестора.
В главе 6 приведены основные характеристики портфеля ценных бумаг. Оценены эффективность и риск портфеля ценных бумаг для случаев, когда ценные бумаги некоррелированные, коррелированные и антикоррелированые.
В главе 7 рассмотрена задача Г. Марковица (H. Markovitz) оптимизации портфеля ценных бумаг. Приведено аналитическое решение задачи для случая, когда нет ограничений в виде неравенства, и описаны численные методы решения задач оптимизации в общем случае.
В главе8 рассмотрена задача Д. Тобина (D. Tobin) оптимизации портфеля инвестора в случае, когда ценные бумаги разбиты на две группы: безрисковых и рискованных ценных бумаг. Приведены аналитическое и численное решение задачи. Приведены примеры расчета коэффициентов Шарпа.
|
|
|
В главе 9описаны статистические методы анализа фондового рынка: прямой статический подход и метод ведущего фактора.
В приложении приведены сведения из теории вероятности и математической статистики необходимые для понимания пунктов 3.6 и 4.5 и разделов с 5 по 9.
ТОВАРЫ ФИНАНСОВОГО РЫНКА
Инвестиции в широком смысле слова означают «расстаться с деньгами сегодня, чтобы получить большую их сумму в будущем». Точнее инвестиция (англ. investment) – долгосрочное вложение капитала инвестором в объекты предпринимательской и других видов деятельности, в результате которого образуется прибыль (доход) и достигается социальный эффект. Инвестиция может осуществляться как внутри страны, так и за границей.
Реальные инвестиции – инвестиции в какой – либо тип материально осязаемых активов, таких, как земля, оборудование, заводы и т.д.
Финансовые инвестиции – инвестиции в какие – либо ценные бумаги.
Значительная часть пособия посвящена количественным методам оценки финансовых инвестиций. Рассмотрим основные товары финансового рынка.
Финансовый рынок – это рынок, где товарами являются сами деньги, банковские кредиты, ценные (денежные) бумаги и финансовые услуги.
Финансовый рынок соответственно делится на денежный рынок и рынок капитала, который делится на кредитный и фондовый рынок. Основным предметом нашего исследования будет фондовый рынок (security packet), т. е. рынок ценных бумаг.
Ценная бумага – это юридический документ на право собственности, на доход или совершение какой-либо сделки.
Ценные бумаги могут быть: на предъявителя, именные и ордерные (в этом случае фиксированы, кто выдал и кто предъявляет ценную бумагу). Среди ценных бумаг выделяют две группы: первичные и вторичные ценные бумаги.
Первичные ценные бумаги являются правами на имущество, денежные средства, продукцию, землю и другие первичные ресурсы. К первичным ценным бумагам относят облигации, акции, государственные долговые обязательства, векселя, депозитные сертификаты.
Облигации или долговые обязательства (от лат. obligatio – обязательства) – ценная бумага, удостоверяющая отношение займа между кредитором, владеющим облигацией, и должником – эмитентом облигации. Облигация удостоверяет внесение ее владельцем денежных средств и подтверждает обязательство возместить ему номинальную стоимость облигации в заранее установленный срок, с уплатой фиксированного процента (fixed income securities) или иное предусмотренное условиями выпуска.
Выпускаются облигации внутренних государственных и местных займов и облигации предприятий. Они могут быть именными, на предъявителя, процентными и беспроцентными, свободно обращающими или с ограниченным кругом обращения. В зависимости от длительности действия существуют облигации краткосрочные (до 3 лет), среднесрочные (от 3 до 7 лет), долгосрочные (от 7 до 20 лет), бессрочные. Облигации бывают обычными или конвертируемыми, которые могут быть обменены в любой момент на акции. Способы обеспечения облигаций: имущественный залог, залог от доходов будущей деятельности, залог гарантийных обязательств.
Доход по облигации выплачивается путем оплаты их купонов или при погашении займов начислением процентов к номиналу. Точнее, по способу формирования дохода облигации подразделяются на облигации, у которых:
‑ фиксированная процентная ставка (стоимость облигации 1000 руб., доход ‑ 4 %, доход по полугодовому купону – 2 %);
‑ плавающая купонная ставка (обычно привязана к доходности каких - либо других ценных бумаг);
‑ равномерно растущая ставка (на пример для учета инфляции);
‑ нулевой купон (бескупонная, нуль купонная, дисконтная облигация) - пример такой облигации ГКО, МКО.
Чем чаще выплаты, тем выше доходность облигации.
Пример
Номинальная стоимость облигации 1000 руб., срок действия -- 5 лет, годовая процентная ставка 5 %. В этом случае доход при годовой процентной ставке: S1 = 1000 (1+0.05)5 = 1276,3.
При полугодовом купоне имеем S1/2 = 1000 (1+0.025)10 = 1280,1.
Существуют рейтинги корпоративных облигаций со специальными оценками: А++-- - высшего качества, А+-- - очень хорошие, А - хорошие, В++-- - средние, В-- - плохие и пр.
Наибольший интерес для фондового рынка представляют долговые обязательства, которые кредитор может свободно продавать другим лицам. Именно они составляют основную массу средств, обращающихся на фондовом рынке.
Акции (от фр. action) – это ценные бумаги, удостоверяющие право их владельца на долю собственности акционерной кампании, включая право на участие путем голосования в принятии основных решений и право на получение дивидендов из прибылей компании. Акции имеют номинальную, эмиссионную, балансовую, ликвидационную и рыночную (курсовую) цену. Номинальная цена указана на бланке акции, она отражает долю уставного капитала, приходящуюся на одну акцию в момент учреждения общества. Эмиссионная цена – цена, по которой акция продается при первичном размещении. Балансовая цена – это цена, рассчитанная по балансу, как отношение стоимости чистых активов к общему числу выпущенных акций. Ликвидационная цена определяется в момент ликвидации акционерного общества. Рыночная (курсовая) цена – та цена, по которой акция котируется на фондовом рынке.
По условиям выплаты дивидендов акции бывают:
- привилегированными, они не дают акционеру право на участии в управлении АО и дают акционеру преимущественное право на получение фиксированных дивидендов, которые выплачиваются до того, как распределяют дивиденды по обычным акциям;
- обычными акциями, которые дают право на участие в управлении АО, при этом размер выплачиваемых дивидендов зависит от финансовых результатов деятельности АО и решений собрания акционеров.
Акции в отличие от облигаций выпускаются на бессрочный период. В случае банкротства АО акционеру возвращается ликвидационная стоимость акции.
Акции компаний открытого типа являются свободно продаваемыми и покупаемыми и представляют собой наиболее активную часть фондового рынка.
Пример
Уставной капитал АО равен 400 млн. Выпущено 1 млн обычных и 1 млн привилегированных акций с дивидендом 8 %. Чистая распределяемая прибыль АО равна 40 млн. На привилегированные акции приходится 200 млн уставного капитала. Тогда сумма выплат по привилегированным акциям составит 200*0,08 = 16 млн. Остаток 24 млн будет потрачен на выплаты по обычным акциям. Тогда доходность обычных акций равна 24 / 200 = 12 %.
Вексель (от нем. Wechsel) – ценная бумага, удостоверяющая безусловное денежное обязательство векселедателя уплатить по наступлении срока определенную сумму денег владельцу векселя. Участие банков в вексельном обращении заключается в предоставлении векселедержателю дисконтного кредита путем покупки векселя до срока.
Государственные долговые обязательства – ценные бумаги, удостоверяющие отношения займа, в которых должником выступает государство, органы государственной власти и управления.
Депозитный сертификат банка – обязательство банка по выплате размещенных у него депозитов.
Производные (вторичные) ценные бумаги – это ценные бумаги, удостоверяющие право владельца на покупку или продажу первичных ценных бумаг. К ним относятся: опционы, фьючерсы, варранты, подписные права и т. д.
Опцион (от нем. option – выбор) – привилегия, приобретаемая при уплате известной премии на бирже, на покупку или продажу товара по заранее установленной цене в определенный момент времени (европейский опцион) или вплоть до определенного времени (американский опцион). Товаром может быть что угодно (золото, иностранная валюта, акции и т. п.). Риск покупателя опциона ограничен премией, выплаченной за опцион, риск продавца опциона снижается на величину полученной премии.
Опцион дает право совершить определенную сделку, причем условия сделки не являются обязательными. Опционы бывают двух типов: опцион на право покупки - опцион колл (coll) и опцион на право продажи - опцион пут (put).
Пример
Инвестор А рассчитывает на повышение курса акций, инвестор В рассчитывает на понижение курса. Текущий курс акций $ 30. А покупает у В опцион на покупку через 3 месяца пакета из 100 акций по цене $ 35. За это право А платит В премию (цену опциона) в размере $ 200.
Если курс повышается и становится $ 40, то А покупает акции по $ 35 и имеет возможность продать их по $ 40. Тогда его чистая прибыль составит
(40 – 35)*100 – 200 = $ 300 при затратах $ 200. Доходность операции составит 300 / 200 = 150 %.
Если А не покупает опцион на покупку, а покупает акции по $ 30 в начале и продает по $ 40 через 3 мес., то прибыль равна (40 – 30) * 100=$1000, а доходность 1000/3000 = 33 %.
Если курс акций падает, то А их не покупает и теряет $ 200.
Таким образом, у покупателя опциона доходы могут быть сколь угодно большими, а расходы не превышают цены опциона. В то же время у продавца ситуация обратная: его возможный выигрыш не превосходит цены опциона, проигрыш может быть очень большим. Однако продавец опциона сознательно рисковал, надеясь на понижение курса акций.
Следует отметить, что опционы являются примерами стратегий хеджирования, так как купив пакет акций и опцион на их продажу можно обезопасить себя от значительных потерь, связанных с падением курса акций.
Контракт на поставку в будущем (фьючерс, от англ. futures) – это обязательство продавца поставить к определенной дате определенное количество товара в определенное место по ценам, фиксируемым в момент заключения сделки. Под товаром может пониматься реальный товар (зерно, мясо, нефть и т. д.), либо ценные бумаги, например, акции.
Вместе с тем, фьючерс сам по себе является товаром на фондовом рынке вплоть до даты его исполнения. В отличие от опциона фьючерс – ценная бумага, которая дает право совершить определенную сделку, условия которой обязательны. В связи с этим опцион всегда дороже фьючерса.
Варрант (от англ. warrant – полномочие) – доверенность (свидетельство), выдаваемая складом владельцу товара. Состоит из двух частей – квитанции и собственно варранта. Относится к ценным бумагам, так как он может быть продан, передан, заложен. С передачей варранта новый владелец приобретает право на товар. Товаром могут быть и акции.
Поскольку цены контрактов, опционов, варрантов и т. д. зависят от цен фигурирующих в них товаров, то их называют производными ценными бумагами. Число этих бумаг постоянно растет.
Действующими лицами на фондовом рынке являются:
- эмитенты (от лат. emittere – выпускать), т. е. организации, выпускающие ценные бумаги (обычно это обладатели средств производства);
- инвесторы (от англ. investment), т. е. владельцы, вкладывающие капитал в ценные бумаги;
- посредники – брокерские конторы (от англ. broker), фондовые биржи, инвестиционные фонды, банки, осуществляющие продвижение ценных бумаг от эмитентов к инвесторам.
Саморегуляцию и устойчивость фондовому рынку обеспечивают:
- спекулянты, играющие на «времени», т. е. получающие прибыль от правильного прогноза цен на ценные бумаги;
- арбитражеры, играющие на разнице цен одновременно на нескольких биржах;
- хеджеры, заключающие сделки с гарантией, страхующие клиентов от возможного разорения.
Целью каждого участника фондового рынка является приумножение капитала.
В настоящее время выбор правильной стратегии вложения денег в условиях разнообразия возможностей практически не возможен без использования специальной науки – финансового анализа, элементы которого будут рассмотрены в данной работе.
ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ
В финансовом анализе огромную роль играет время. Эта роль велика даже при малой инфляции, а при большой инфляции она является решающей. Все знают на собственном опыте, что 100 тыс. руб. сегодня и через месяц могут оказаться различными деньгами. Например, при запланированной инфляции 20 % приведенная выше сумма в 100 тыс. руб., если держать ее дома, через год превратится в 100(1-0,2)=80 тыс. руб. Второй пример, предположим, что вам должны вернуть долг в 100 тыс. руб. и рассматриваются два варианта возврата денег. В первом варианте предлагают его отдать по частям: 50 тыс. руб. через полгода и остальные 50 тыс. руб. через год. Во втором варианте предполагается возврат всей суммы сразу через год. Очевидно первый вариант для кредитора лучше.
С другой стороны, если у вас имеются накопления в рублях, долларах, евро, иенах, юанях и т. д. или в ценных бумагах, то в каждый момент времени эти накопления имеют разную курсовую стоимость. Последнее особенно ощутимо в условиях кризиса.
В связи с этим в финансовых вычислениях чрезвычайно важно учитывать время. Поэтому, в частности, в экономических расчетах денежные суммы нельзя просто так складывать, без учета зависимости капитала от времени. Ниже будут приведены методы, позволяющие учесть зависимость капитала от времени в финансовых вычислениях.
Ценная бумага удостоверяет определенную финансовую операцию (сделку). Не конкретизируя вид ценной бумаги, изложим основные математические методы, позволяющие оценить выгодность и эффективность данной операции (сделки). В примерах и задачах будут приведены варианты расчетов эффективности для основных видов ценных бумаг.
Основные понятия
Простейшей финансовой операцией является однократное предоставление в долг некоторой суммы. В этой сделке присутствуют два лица – кредитор и дебитор. Эта финансовая операция характеризуется следующими временными параметрами и денежными величинами.
Пусть функция S(t) описывает зависимость капитала S от времени t. Простейшая финансовая сделка сводится к однократному предоставлению в долг некоторой суммы S(t) с условием возврата суммы S(t+T) через время Т.
Для оценки эффективности операции используются два показателя:
- относительное приращение суммы или капитала (процентная ставка, процент, ставка процента, рост, норма прибыли, доходность, интерес, interest rate, return)
, (2.1)
отсюда
; (2.2)
- относительная скидка или относительное уменьшение конечного капитала (учетная ставка, дисконт, discount rate)
, (2.3)
отсюда
, (2.4)
где S(t) – капитал в начальный момент t (начальный вклад);
S(t+T) – капитал в конечный момент t+T (конечная сумма).
Таким образом, в любой финансовой операции присутствуют три величины, две из которых заданы, а одна неизвестна. В соответствии с этим возникают различные экономические задачи, которые будут рассмотрены ниже. Наличие двух показателей эффективности процентной ставки r и дисконта d связано с тем, что процесс наращивания и процесс дисконтирования отличаются направлением потока денежных средств.
 | |||
 |
Рис. 2.1
Если время сделки Т постоянно, то Т называют базовым периодом, а rT – часто называют процентной ставкой и dT – дисконтом. Очевидно, процентная ставка и дисконт не являются независимыми показателями эффективности сделки. Они связаны соотношениями:
. (2.5)
Вместо дисконта иногда используют математический дисконт фактор, равный
. (2.6)
Очевидно
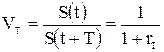. (2.7)
Рост и дисконт являются безразмерными величинами и обычно выражают в процентах.
Пример 1.
Ссуда в размере 2 млн руб. дана на 1 год с условием возврата 4 млн руб. В этом случае процентная ставка равна:
,
дисконт равен 
.
Пример 2.
Кредит выдан на 5 млн руб. с кредитной ставкой 50 % годовых. Тогда, через год следует вернуть:
млн руб.
Пример 3.
Кредит выдан с условием возврата через год 5 млн руб. и дисконтом 30 %. Тогда дебитор получит:
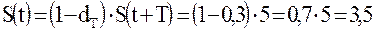млн руб.
При этом дисконт фактор равен 
.
Задача 1.
Предприниматель обратился в банк с просьбой о предоставлении ссуды в размере 1млн руб. на срок 1 год. Банк выделил ему эту ссуду с годовой учетной ставкой 20 %. Определить сумму, возвращаемую предпринимателем банку через год.
Ответ.
1,25 млн руб.
Для удобства сравнения финансовых операций процентные ставки, дисконт приводят к базовому периоду – обычно году. Отсюда возникает задача: имея процентные ставки и дисконт за базовый период Т, вычислить соответствующие величины за фактический период действия сделки.
Правила начисления процентов оговариваются при заключении сделки и сводятся к схемам простых процентов (simple interest), сложных процентов (compound interest) и смешанных процентов. Суть данных схем заключается в следующем.
Кредитование
Простые ставки процентов. Пусть начальный момент равен нулю, Т – базовый период, t – фактический период действия сделки, называемый конверсионным периодом или периодом начисления, S(o) – начальная сумма, S(t) – конечная сумма, получаемая кредитором в момент t. Если годовой интерес (ставка) равна r, то в конце фактического срока сделки t дебитор должен заплатить кредитору сумму
, (2.8)
где t и Т измеряются в днях. При этом согласно договору, используется либо точная длительность года – 365 или 366 дней (точные проценты), либо приближенная длительность года – 360 дней = 12 месяцев ´30 дней (обычные проценты).
В ряде случаев удобно использовать упрощенную форму записи формулы простых процентов в виде:
, (2.9)
где фактический период действия сделки t измеряются в годах. При этом переход от длительности сделки в днях к длительности сделки в годах производится по схемам обычных или точных процентов.
Таким образом, в формуле (2.9), описывающей финансовую операцию, присутствуют четыре параметра. Можно задать любые три параметра, а четвертый параметр считать неизвестным. Определить его можно из уравнения (2.9).
В соответствии с этим возникают различные экономические задачи, которые будут рассмотрены ниже.
Пример 4.
Выдан кредит на сумму 2 млн руб. с 15.01.2010 г. по 15.03. 2010 г. под
40 % годовых. В зависимости от договора сумма погасительного платежа различна. При точном расчете t=16 дней (январь) + 28 дней (февраль) +15 дней (март) = 59 дней согласно (2.8) имеем:
млн руб.
Приближенный расчет по обычным процентам дает согласно (2.8) t=60 дней:
млн руб.
Сумма платежа по обычным процентам всегда больше чем по точным процентам.
Пример 5.
Определить простую ставку процентов, при которой первоначальный капитал в размере 60 млн руб. достигнет 63 млн руб. через квартал.
Из формулы простых процентов (2.9) для ставки r имеем:
Подставляя соответствующие числовые значения, получим:
Пример 6.
Определить период начисления, за который первоначальный капитал в размере 38 млн руб. вырастет до 40 млн руб., если используется простая ставка процентов 12 % годовых.
Из формулы простых процентов (2.9) для времени t имеем:
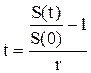
Тогда, подставляя соответствующие числовые значения, получим:
Пример 7.
Кредит выдается под простую ставку 16 % годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 50 млн руб.
Из формулы простых процентов (2.9) имеем:
Следовательно, сумма, получаемая заемщиком равна:
S(0)=50/(1+0,16·250/360)= 45 млн руб.,
Сумма процентных денег равна 5 млн руб.
Задача 2.
Ссуда в размере 50 тыс. руб. выдана на полгода по простой ставке процентов 28 % годовых. Определить наращенную сумму.
Ответ.
57 тыс. руб.
Задача 3.
Кредит в размере 10 млн руб. выдан 2 марта до 11 декабря под 30 % годовых, год високосный. Определить размер наращенной суммы для различных вариантов расчета процентов: точное число дней ссуды и точная длительность года 366 дней; точное число дней ссуды и приближенная длительность года 360 дней; приближенные число дней ссуды и длительность года.
Ответ.
12327868 руб.;
12366666 руб.;
12333333 руб.
Задача 4.
Определить период начисления, за который первоначальный капитал в размере 25 млн руб. вырастет до 40 млн руб., если используется простая ставка процентов 28 % годовых.
Ответ.
t=2,14 года.
Задача 5.
Определить простую ставку процентов, при которой первоначальный капитал в размере 24 млн руб. достигнет 30 млн руб. через год.
Ответ.
r=25 %.
Задача 6.
Кредит выдается под простую ставку 26 % годовых на 250 дней. Рассчитать сумму, получаемую заемщиком, и сумму процентных денег, если требуется возвратить 40 млн руб.
Ответ.
33,955857 млн руб.;
6,044143 млн руб.
Задача 7.
В течение первого месяца цена товара увеличилась на 25 %, а в течение следующего месяца цена товара возвратилась к первоначальному уровню. На сколько процентов уменьшилась новая цена товара?
Ответ.
На 20 %.
Задача 8. Переменная ставка простых процентов.
За время хранения вклада меняются величины процентных ставок. Пусть в периоды времени n1, n2, … nm процентные ставки составляют r1, r2,… rm. Найти наращенную сумму S(t), если начальный вклад равен S(0).
Ответ.
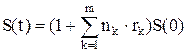
При расчетах по среднесрочным и долгосрочным кредитам используется схема сложных процентов.
Сложные проценты. Пусть длительность сделки t кратна базовому периоду Т, т. е. t целое число. При базовом периоде Т = 1 год, длительность сделки целое число лет t. Тогда наращенная сумма равна:
, (2.10)
где
S(0) – начальная сумма,
r – процентная ставка за год (интерес).
Очевидно, что зависимость суммы S(t) от времени t при расчете по схеме простых процентов (2.9) линейная, при расчете по схеме сложных процентов нелинейная (является показательной функцией от t), и, как будет показано ниже, в ряде случаев эта зависимость хорошо апроксимируется экспонентой.
Формула (2.10) может использоваться для расчета по сложным процентам при любой длительности сделки t так, как показательная функция определена при любых значениях t.
Пример 8.
Первоначальная вложенная сумма равна 200 тыс. руб. Определить наращенную сумму через пять лет при использовании простой и сложной ставки процентов в размере 28 % годовых. Рассмотреть случаи, когда сложные проценты начисляются ежегодно, по полугодиям и поквартально. Для простых процентных ставок имеем:
тыс. руб.
Для сложных годовых процентов:
тыс. руб.
Для сложных полугодовых начисленных процентов:
тыс. руб.
Для поквартального начисления сложных процентов:
тыс. руб.
Обобщая пример 5, рассмотрим задачу вычисления процентной суммы S(t) через t лет в случае, когда проценты начисляются m раз в год. Сумма S(o) выдана под r процентов годовых с начислением сложных процентов m раз в год. Воспользовавшись формулой (2.10), для этого случая очевидно имеем:
. (2.11)
Представляет интерес рассмотрения предельного случая при m®¥, тогда сложные проценты начисляются непрерывно. Используя замечательный предел
,
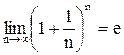где 
– основание натуральных логарифмов (число «е»), получим:
.
Таким образом, если сложные проценты начисляются непрерывно, наращенная сумма экспоненциально зависит от време
|
|
|
