 |
Непрерывная ставка (сила роста) и непрерывный дисконт
|
|
|
|
Дискретная процентная ставка – это ставка, при которой процент начисляется за заранее установленные, или определенные, периоды. Если уменьшить период начисления процентов до бесконечно малой величины (период, за который будут произведены начисления, стремится к нулю, а количество начислений процентов – к бесконечности), то проценты будут начисляться непрерывно. В этом случае процентная ставка называется непрерывной ставкой или силой роста.
В теоретических исследованиях и на практике, когда платежи производятся многократно, удобно использовать непрерывный способ начисления процентов. Переход к пределу может быть осуществлен аналогично тому, как это делалось в пункте 2.2 при выводе формулы (2.12) или следующим способом.
Непрерывная ставка может быть постоянной или изменяющейся. Рассмотрим случай, когда непрерывная процентная ставка в разные моменты времени различна.
Пусть, а(t) – функция, описывающая зависимость непрерывной ставки (силы роста) от времени t. Приращение капитала S(t) в момент t за промежуток времени Δt равно:
S(t + Δt) – S(t) = a(t) Δt S(t)
Тогда, имеем:
При Δt →0 получим, что скорость изменения капитала пропорциональна капиталу. Тогда, сумма платежа (капитал) S(t) удовлетворяет линейному однородному дифференциальному уравнению первого порядка:
, (2.28)
где
– скорость изменения платежа (скорость изменения капитала);
S(t) - сумма платежа (капитал);
a(t) – непрерывный процент начисления или сила роста.
В другом виде уравнение запишется:
dS = a(t) S dt, (2.29)
т. е. приращение платежа пропорционально самому платежу S и приращению времени dt. Коэффициент пропорциональности а(t) суть сила роста или процент начисления.
|
|
|
Возможна еще одна запись дифференциального уравнения:
, (2.30)
т. е. относительное приращение суммы платежа dS/S пропорционально приращению времени dt. Причем по-прежнему, а(t) определяется процентами начисления и в общем случае может зависеть от времени. Все три уравнения для капитала (2.28), (2.29), (2.30) эквивалентны.
Рассмотрим некоторые простейшие свойства капитала, описываемого дифференциальным уравнением (2.28)-(2.30). Если функция a(t)>0 положительна, то при положительном капитале S>0 производная от капитала dS/dt >0 также положительна и, следовательно, капитал S(t) растет. В этом случае a(t) называется непрерывным процентом начисления или силой роста.
В противном случае если функция a(t)<0 отрицательна, то при положительном капитале S>0 производная от капитала dS/dt<0 отрицательна и, следовательно, капитал S(t) убывает. В этом случае абсолютная величина |a(t)| называется непрерывным дисконтом.
Решение линейного дифференциального уравнения хорошо известно. Действительно, уравнение (2.30) является уравнением с разделяющимися переменными и его можно проинтегрировать:
Вычислив интеграл, получим:
,
где 
- неопределенный интеграл от a(t),
С1- произвольная постоянная.
Отсюда, имеем:
Окончательно, общее решение дифференциального уравнения запишется в виде:
, (2.31)
где 
- новая произвольная постоянная.
Для определения произвольной постоянной С нужно знать капитал хотя бы в один какой-нибудь момент времени. Если известно что в момент времени t=t0 капитал равен S = S0 (т. е. S(t0)=S0), то произвольная постоянная С легко определяется из (2.31):
,
или
Подставляя полученный результат в (2.31), имеем:
.
Воспользовавшись классической формулой связи определенного и неопределенного интеграла (формулой Ньютона – Лейбница):
,
получим решение дифференциального уравнения с начальными условиями S(t0)=S0 в виде:
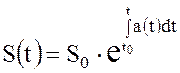
Часто отсчет времени можно производить от начального момент, тогда t0=0 и решение линейного дифференциального уравнения записывается в виде:
|
|
|
, (2.32)
где
S(0) – начальная сумма в момент 0;
S(t) – сумма платежа в момент t.
Очевидно, приведенные формулы при a(t)>0 соответствуют расчету кредитования, а при a(t)<0 – расчету дисконтирования.
Если сила роста постоянна на всем рассматриваемом промежутке времени, т. е. a(t)= r, то для конечного платежа в момент t имеем:
. (2.33)
Очевидно, эта формула совпадает с полученной ранее предельным переходом формулы для непрерывных процентов (2.12).
Рассмотрим некоторые примеры использования данных формул.
Пример 28.
Ссуда 200 тыс. руб. дана на 2,5 года под ставку 20 % годовых с ежеквартальным начислением. Найти сумму конечного платежа. Расчет произвести по дискретным и непрерывным процентам.
Решение.
Сумма конечного платежа удовлетворяет дифференциальному уравнению 
, где r=20 %=0,2 в соответствии с процентом ежегодного начисления и время t измеряется в годах. Решение линейного уравнения известно:
.
Тогда сумма конечного платежа равна:
тыс. руб.
Расчет для дискретного случая по формулам (2.11) дает:
тыс. руб.
Видно, что при многократных начислениях небольших процентов результаты расчетов сумм конечного платежа близки.
Рассмотрим теперь пример расчета дисконтирования в непрерывном случае.
Пример 29.
Вексель на 3 млн руб. с годовой учетной ставкой 10 % и дисконтированием 2 раза в год выдан на 2 года. Найти исходную сумму, которая должна быть выдана в долг под этот вексель. Расчет произвести по дискретным и непрерывным процентам.
Решение.
Одолженная под вексель сумма платежа удовлетворяет линейному дифференциальному уравнению, решение которого известно:
.
Тогда:
млн руб.
Расчет одолженной под вексель суммы по дискретным формулам (2.24) дает близкие результаты:
млн руб.
Таким образом, теоретические и практические вычисления по непрерывным формулам дают результаты, близкие к результатам расчета по дискретным формулам, если количество начислений велико, а процент начисления невелик.
|
|
|
