 |
Контрольные вопросы и задания. Тема 2.6. Изгиб. Классификация видов изгиба. Внутренние силовые факторы при изгибе. Основные определения
|
|
|
|
Контрольные вопросы и задания
1. Определите крутящий момент в сечении 2-2 (рис. 28. 6).
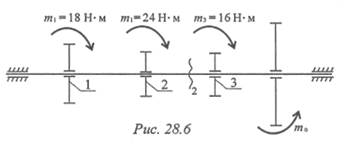
2. В каком порядке рациональнее расположить шкивы, чтобы получить минимальную нагрузку на вал? Использовать схему рис. 28. 6.
3. Как изменится напряжение в сечении, если диаметр вала уменьшить в два раза?
4. Проведены расчеты вала на прочность и жесткость. Получено: диаметр вала из расчета на прочность 65 мм, диаметр вала из расчета на жесткость 70 мм. Каким должен быть вал?
5. Как изменится угол закручивания вала, если крутящий момент увеличить в 4 раза, а диаметр уменьшить в 2 раза?
6. Напишите условия прочности и жесткости при кручении.
Тема 2. 6. Изгиб. Классификация видов изгиба 239
ЛЕКЦИЯ 29
Тема 2. 6. Изгиб.
Классификация видов изгиба.
Внутренние силовые факторы при изгибе
Иметь представление о видах изгиба и внутренних силовых факторах.
Знать методы для определения внутренних силовых факторов и уметь ими пользоваться для определения внутренних силовых факторов при прямом изгибе.
Основные определения
Изгибом называется такой вид нагружения, при котором в поперечном сечении бруса возникает внутренний силовой фактор —
изгибающий момент.
 Брус, работающий на изгиб, называют балкой.
Брус, работающий на изгиб, называют балкой.
Изображен брус, закрепленный справа (защемление), нагруженный внешними силами и моментом (рис. 29. 1).
Плоскость, в которой расположены внешние силы и моменты, называют силовой плоскостью.
Если все силы лежат в одной плоскости, изгиб называют плоским.
Плоскость, проходящая через продольную ось бруса и одну из главных осей его центральных поперечного сечения, называется главной плоскостью бруса.
|
|
|
240 Лекция 29
Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют прямым (рис. 29. 1).
Если силовая плоскость не проходит через главную плоскость бруса, изгиб называют косым изгибом (рис. 29. 2).

Внутренние силовые факторы при изгибе
Пример 1. Рассмотрим балку, на которую действует пара сил с моментом ти внешняя сила F (рис. 29. 3а). Для определения внутренних силовых факторов пользуемся методом сечений.
Рассмотрим равновесие участка 1 (рис. 29. 36).
Под действием внешней пары сил участок стремится развернуться по часовой стрелке. Силы упругости, возникающие в сечении 1, удерживают участок в равновесии.
Продольные силы упругости выше оси бруса направлены направо,
Тема 2. 6. Изгиб. Классификация видов изгиба 241
а силы ниже оси направлены налево. Таким образом, при равновесии участка 1 получим: Σ FZ = 0. Продольная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в сечении 1-1 относительно оси Ох:

Этот момент называют изгибающим моментом Мх = Ми.

Из схемы вала на рис. 29. 3b видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.
Такой слой называют нейтральным слоем (НС). Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.
Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.
|
|
|
Практически величина изгибающего момента в сечении определяется из уравнения равновесия: 
242 Лекция 29
Таким образом, в сечении 1-1 продольная сила равна нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29. 3в).
Запишем уравнения равновесия для участка бруса:
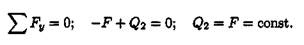
В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг. 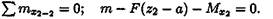
Изгибающий момент в сечении: МХ2 = т - F(z2 — a);
z2 — расстояние от сечения 2 до начала координат.
Изгибающий момент зависит от расстояния сечения до начала координат.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
|
|
|


