 |
Решение. Контрольные вопросы и задания. Тема 2.6. Изгиб. Определение внутренних силовых факторов. Реакция в опоре направлена в обратную сторону.
|
|
|
|
Решение
1. Определение реакций в опорах. Уравнения равновесия:
Σ mA = 0; -F1 · 6 + m- RB · 10 + F2 · 12 = 0; -35 · 6 + 80 - RB · 10 + 70 · 12 = 0;
250 Лекция 30

Реакция в опоре направлена в обратную сторону.
Проверка: Σ Fy = 0;
-RA + F1 + RB - F2 = 0; -36 + 35 + 71 - 70 = 0.
Реакции определены верно.
2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.
Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр. -
Участок 1 (от точки А до точки С).
Тема 2. 6. Изгиб 251
В точке А приложена реакция Ra, направленная вниз. Поперечная сила на участке постоянна: Q1 = Ra = - З6кН.
Момент в точке А равен нулю.
Точка С (слева). Приложена внешняя сила F1 = З5кН, направленная вверх, — здесь возникнет скачок вверх на величину З5кН. Момент в точке С (слева) может быть рассчитан по известной зависимости МСслева =-RA · 6; МСслева =-36·6 =-216 кН· м.
Участок 2 (от точки С справа до точки В).
Поперечная сила в точке С (справа) равна Qc = -Ra + F1; Qc = -36 + 35 = -1кН.
В точке С приложена внешняя пара сил с моментом 80кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: Мcсправа = МСслева+ m; Мcсправа = -216 + 80 = 136кН·м.
Поперечная сила на втором участке постоянна: Q2 = Qcсправа.
Момент в точке В определяется по зависимости
МB = -RA • 10 + F1 • 4 + m; MB = -36 • 10 + 35 • 4 + 80 = -140 кН•м.
|
|
|
Справа и слева от точки В момент имеет одинаковые значения.
Участок 3 (от точки В (справа) до точки D).
В точке В приложена внешняя сила Rb. Здесь появляется скачок на величину 71 кН, QB = -1 + 71 = 70 кН.
Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т. к. здесь не приложена внешняя пара сил: MD = 0.
Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.
По полученным значениям сил и моментов строим эпюры (эпюры под схемой вала, рис. 30. 4).
Контрольные вопросы и задания
1. Определите величины поперечных сил в сечении 1 и в сечении 2 (рис. 30. 5).

2. Напишите формулу для расчета изгибающего момента в сечении 3 (рис. 30. 6).
252 Лекция 30

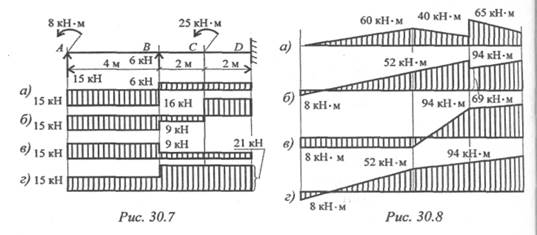
3. Из представленных эпюр выберете эпюру поперечной силы для изображенной балки (рис. 30. 7).
Пояснения.
A. Обратить внимание на знак силы в сечении 1 (знак +).
Б. Обратить внимание на величину скачков в местах приложения внешних сил.
B. Приложение момента пары сил не должно отражаться на
эпюре Q.
4. По рис. 30. 8 выбрать эпюру изгибающего момента для изображенной на рис. 30. 7 балки.
Пояснения.
A. На конце бруса приложен момент пары, следовательно, в этом
месте изгибающий момент должен быть равен этому же значению.
Б. Обратить внимание на знак момента в сечении 1.
B. В точке А приложена также и сила, поэтому линия, очертившая
Тема 2. 6. Изгиб 253
эпюру, должна быть наклонной.
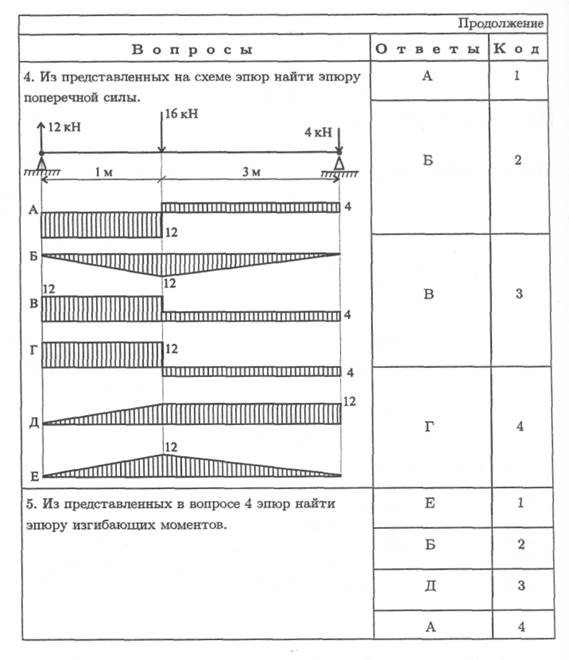
5. Ответьте на вопросы тестового задания.
Тема 2. 6. Изгиб.
Определение внутренних силовых факторов
|
|
|

254 Лекция 30
 Тема 2. 6. Изгиб 255
Тема 2. 6. Изгиб 255
ЛЕКЦИЯ 31
Тема 2. 6. Изгиб.
Построение эпюр поперечных сил и изгибающих
моментов. Приложены сосредоточенные и распределенные
нагрузки
Знать дифференциальные зависимости между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом, основные правила построения эпюр.
Уметь строить эпюры поперечной силы и изгибающего момента в случае приложения сосредоточенных и распределенных нагрузок.
Примеры решения задач
Пример 1. Одноопорная балка нагружена сосредоточенными силами и распределенной нагрузкой (рис. 31. 1). Построить эпюры поперечных сил и изгибающих моментов.
|
|
|


