Построение эпюр.   Контрольные вопросы и задания. Тема 2.6. Изгиб. Нормальные напряжения при изгибе. Расчеты на прочность

Построение эпюр

Анализируем схему балки.

Рассмотрим участок 1 до сечения 1.

В опоре А действует сосредоточенная сила Ra = 7, 2 кН. На участке 1 поперечная сила остается постоянной: Q1 = Ra = 7, 2 кН (рис. 31. 3).

         

Изгибающий момент в точке А равен нулю, т. к. здесь нет мо­мента внешней пары сил: Ма = 0.

Момент в точке С (граница участка, z — 4м) Мс = Ra • 4; М_с = 7, 2 -4 = 28, 8кН • м.

Эпюра очерчивается прямой линией, наклонной к оси Oz (рис. 31. 3).

260                                                                  Лекция 31

Рассмотрим участок 2 (рис. 31. 3). Здесь действует распределен­ная нагрузка интенсивностью q = 4кН/м. При перемещении вдоль оси балки направо распределенная нагрузка суммируется. Эпюра Q2— прямая линия, наклонная к оси Oz. Распределенная нагруз­ка направлена вниз (см. Основные правила построения эпюр, п. 4), здесь эпюра изгибающего момента очерчена параболой, обращенной выпуклостью вверх.

Реакция в опоре Ra и распределенная нагрузка направлены в разные стороны. Следовательно, возможна точка, в которой, по пра­вилу 2, Q2 = 0, а изгибающий момент экстремален.

Для построения эпюры моментов необходимо составить уравне­ние поперечной силы на участке 2 и приравнять величину попереч­ной силы нулю. Из уравнения можно определить координату точки, в которой изгибающий момент экстремален.

Проводим необходимые расчеты, определяем величины попереч­ных сил и изгибающих моментов в характерных точках.

Рассмотрим участок 2, сечение 2 (рис. 31. 3).

Уравнение поперечной силы Q2 = Ra — q(z2— 4) = 0.

Откуда: 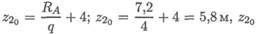  — координата

точки, где изгибающий момент экстремален, т. к. Q2 = 0.

  Уравнение момента на участке 2:

Максимальное значение изгибающего момента на участке 2                                    

                      

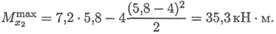
Значения    поперечной    силы    и    изгибающего    момента    в    точке  В:   Q_B = R_B = 16, 8 кН; М_В = 0.

Строим эпюру поперечной силы. Первый участок — прямая ли­ния, параллельная оси Oz. В точке С эпюра становится наклонной. Строим эпюру изгибающих моментов (рис. 31. 3).

Участок 1 эпюра — прямая линия; Ма = 0; Мс — 28, 8 кН • м.

Участок 2 эпюра — парабола с    экстремумом    в    точке  z = 5, 8 м;

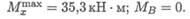
                                                                         Тема 2. 6. Изгиб                                                           261

               

           Контрольные вопросы и задания

1. Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?

2. Как определить положение экстремального значения изгиба­ющего момента при действии распределенной нагрузки на участке балки?

3. Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?

4. Определите координату z, в которой поперечная сила равна нулю (рис. 31. 4).

 

 

5. Определите величину изгибающего момента в точке С (z = 5 м), используя схему рис. 31. 4.

262                                                                                 Лекция 32

ЛЕКЦИЯ 32

Тема 2. 6. Изгиб.

Нормальные напряжения при изгибе.

Расчеты на прочность

Знать распределение нормальных напряжений по сечению бал­ки при чистом изгибе, расчетные формулы и условия прочности.

Уметь выполнять проектировочные и проверочные расчеты на прочность, выбирать рациональные формы поперечных сечений.

Деформации при чистом изгибе

При чистом изгибе в сечении возникает только один внутренний силовой фактор — изгибающий момент.

Рассмотрим деформацию бруса, нагруженного внешней парой сил с моментом m (рис. 32. 1а).

При чистом изгибе выполняются ги­потезы плоских сечений и ненадавливаемости слоев.

   Сечения бруса, плоские и перпенди­кулярные продольной оси, после дефор­мации остаются плоскими и перпенди­кулярными продольной оси.

   Продольные волокна не давят друг на друга, поэтому слои испытывают простое растяжение или сжатие.

   Действуют только нормальные на­пряжения.

   Поперечные размеры сечений не ме­няются.

   Продольная ось бруса после дефор­мации изгиба искривляется и образует  дугу

окружности радиуса р (рис. 32. 16). Материал подчиняется закону Гука.

   Можно заметить, что слои, расположенные выше продольной оси, растянуты, расположенные ниже оси — сжаты (рис. 32. 16). Так как деформации по высоте сечения меняются непрерывно, имеется

                                                                  Тема 2. 6. Изгиб                                                                263

слой, в котором нормальные напряжения а равны нулю; такой слой называют нейтральным слоем (НС). Доказано, нейтральный слой проходит через центр тяжести сечения; р — радиус кривизны ней­трального слоя.

Относительное удлинение прямо пропорционально расстоянию слоя до нейтральной оси.

Используем закон Гука при растяжении: σ = Еε.

Получим зависимость нормального напряжения при изгибе от положения слоя:                                                

⇐ Предыдущая50515253545556575859Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: