Контрольные вопросы и задания.   Тема 2.7. Сочетание основных деформаций. Гипотезы прочности. Понятие о сложном деформированном состоянии

Контрольные вопросы и задания

1. Какие внутренние силовые факторы возникают в сечении балки при чистом и поперечном изгибах?

2. Почему при поперечном изгибе в продольных сечениях балки
возникают касательные напряжения?

3. Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?

4. В какой точке поперечного сечения (рис. 33. 8) касательные
напряжения при поперечном изгибе максимальны?

Варианты ответов:

1. А. 2. В. 3. С. 4. D.

5. Выберите верную эпюру распределения нормальных напряжений при изгибе (рис. 33. 9). Напишите формулу для расчета нормальных напряжений при изгибе. Изгибающий момент действует в вертикальной плоскости.

 

              

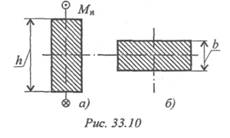
6. Как изменится максимальное нормальное напряжение в сечении (рис. 33. 10а), если   балку  прямоугольного   сечения   положить плашмя (рис. 33. 10б)?  b= 20 мм; h = 100 мм.

7. Во сколько раз увели­чится прогиб балки, если рас­пределенную по всей длине на­грузку заменить сосредоточен­ной, приложенной в середине пролета? Использовать форму­лы для определения прогибов, приведенные в таблице 33. 1.

                      

 

 

278                                                                   Лекция 34

ЛЕКЦИЯ 34

         Тема 2. 7. Сочетание основных деформаций. Гипотезы прочности

Иметь представление о напряженном состоянии в точке упругого тела, о теории предельных напряженных состояний, об эквивалентном напряженном состоянии, о гипотезах прочности.

Знать формулы для эквивалентных напряжений по гипотезам наибольших касательных напряжений и энергии формоизменения.

         Напряженное состояние в точке

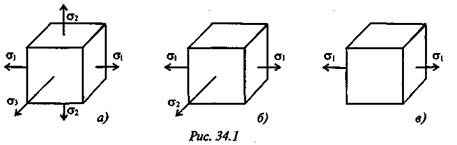
Напряженное состояние в точке характеризуется нормальны­ми и касательными напряжениями, возникающими на всех площад­ках (сечениях), проходящих через данную точку. Обычно достаточ­но определить напряжения на трех взаимно перпендикулярных пло­щадках, проходящих через рассматриваемую точку. Точку принято изображать в виде маленького элемента в форме параллелепипеда (рис. 34. 1).

Положения теории напряженного состояния:

1. Напряженное состояние в данной точке полностью определе­но, если известны напряжения по любым трем взаимно перпендику­лярным площадкам.

2. Среди множества площадок, которые можно провести через данную точку, есть три такие взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения, эти площадки называются главными, а нормальные напряжения, возникающие на них, называются главными напряжениями: σ 1; σ 2; σ 3 (рис. 34. 1).

Одно из этих напряжений — максимально, одно — минимально. Максимальное обозначают σ 1, минимальное — σ 3.

Классификация видов напряженного состояния производится по главным напряжениям:

— если все три главных напряжения не равны нулю, то напря­женное состояние называют объемным (трехосным) (рис. 34. 1а);

— если одно из главных напряжений равно нулю, напряженное состояние называют плоским (двухосным) (рис. 34. 1б);

— если два из главных напряжений ( σ 2= 0 ) противоположны

          Тема 2. 7. Сочетание основных деформаций                              279

 

по знаку, напряженное состояние называют упрощенным плоским состоянием;

— если лишь одно из главных напряжений не равно нулю, на­пряженное состояние линейное (рис. 34. 1в).

            

          Понятие о сложном деформированном состоянии

Совокупность деформаций, возникающих по различным напра­влениям и в различных плоскостях, проходящих через точку, опре­деляют деформированное состояние в этой точке.

Сложное деформированное состояние возникает, если деталь од­новременно подвергается нескольким простейшим нагружениям.

Такие состояния возникают в заклепочных соединениях (срез и смятие), в болтовых соединениях (растяжение и скручивание), при поперечном изгибе бруса (изгиб и сдвиг).

Часто одним из нагружений (незначительным) пренебрегают.

Например, длинные балки рассчитывают только на изгиб.

В ряде случаев нормальные и касательные напряжения, возни­кающие в детали, имеют одинаковый порядок и ими нельзя прене­брегать. Тогда расчет проводят при сложном деформированном со­стоянии.

Сложность расчета заключается в отсутствии эксперименталь­ных данных о предельных напряжениях, т. к. провести испытания из-за множества вариантов нагружения практически невозможно.

Для упрощения расчетов в этом случае применяют теории прочности. Смысл теорий заключается в замене реального слож­ного деформированного состояния равноопасным простым.

Опасное состояние может быть вызвано различными фактора­ми: нормальные напряжения могут достигнуть предела текучести

280                                                Лекция 34

или предела прочности, касательные напряжения могут достигнуть опасного значения или накопленная энергия деформирования может стать слишком большой и вызвать разрушение.

Универсального критерия, позволяющего рассчитать предель­ное состояние для любого материала, нет. Разработано несколько различных гипотез предельных состояний, при расчетах использу­ют наиболее подходящую гипотезу. Расчеты по гипотезам прочности позволяют избегать дорогостоящих испытаний конструкции.

В настоящее время для расчета валов при совместном действии изгиба и кручения используют только третью и пятую теории проч­ности.

Сравнение разнотипных состояний производится с помо­щью эквивалентного {простого) напряженного состояния. Обычно сложное напряженное состояние заменяют простым растяжени­ем (рис. 34. 2).

Расчетное напряжение, соответствующее выбранному од­ноосному растяжению, называют эквивалентным напряжением (рис. 34. 26).

          

Полученное расчетным путем эквивалентное напряжение для точки сравнивают с предельным (рис. 34. 2в).

Напряженное состояние в точке равноопасно эквивалентному напряженному состоянию. Условие прочности получим, сопоста­вив эквивалентное напряжение с предельным, полученным экспе­риментально для выбранного материала:

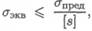где [s] — допускаемый запас прочности.

Как известно, предельным напряжением для пластичных мате­риалов является предел текучести σ _т, а для хрупкого — предел проч­ности σ _в. Предельное    напряженное    состояние    у    пластичных    материалов

        Тема 2. 7. Сочетание основных деформаций                                    281

наступает в результате пластических деформаций, а у хруп­ких — в результате разрушения.

Для пластичных материалов расчет может выполняться по ги­потезе максимальных касательных напряжений: два напряженных состояния равноопасны, если максимальные касательные напря­жения у них одинаковы (третья теория прочности).

Расчет можно проводить и по теории потенциальной энергии формоизменения: два напряженных состояния равноопасны, если энергия формоизменения у них одинакова (пятая теорема прочно­сти).

Для хрупких и хрупко-пластичных материалов применяют тео­рию прочности Мора.

Расчет эквивалентного напряжения для точки по теории макси­мальных касательных напряжений выполняется по формуле

                 

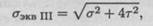
а по теории энергии формоизменения по формуле

                 

где σ — действующее в точке нормальное напряжение; τ — действу­ющее в точке касательное напряжение.

⇐ Предыдущая54555657585960616263Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: