Особенность расчета валов. Примеры решения задач. Решение. Особенность расчета валов

Особенность расчета валов

Большинство валов испытывают сочетание деформаций изгиба и кручения. Обычно валы — прямые брусья с круглым или кольце­вым сечением. При расчете валов касательные напряжения от дей­ствия поперечных сил не учитывают из-за их незначительности.

           Тема 2. 7. Расчет бруса круглого поперечного сечения                        285

Расчеты проводят по опасным поперечным сечениям. При про­странственном нагружении вала пользуются гипотезой независимо­сти действия сил и изгибающие моменты рассматривают в двух взаимно перпендикулярных плоскостях, а суммарный изгибающий момент определяют геометрическим суммированием.

Примеры решения задач

Пример 1. В опасном поперечном сечении круглого бруса воз­никают внутренние силовые факторы (рис. 35. 1) М_х; М_у; M_z.

М_х и М_у — изгибающие моменты в плоскостях уОх и zOx со­ответственно; M_z — крутящий момент. Проверить прочность по ги­потезе наибольших касательных напряжений, если [σ ] = 120 МПа. Исходные данные: М_х = 0, 9 кН∙ м; М_у = 0, 8 кН•м; M_z = 2, 2 кН • м; d = 60 мм.

Решение

Строим эпюры нормальных напряжений от действия изгибаю­щих моментов относительно осей Ох и Оу и эпюру касательных напряжений от кручения (рис. 35. 2).

             

 

Максимальное касательное напряжение возникает на поверхно­сти. Максимальные нормальные напряжения от момента М_х возни­кают в точке А, максимальные нормальные напряжения от момента М_у в точке В. Нормальные напряжения складываются, потому что изгибающие моменты во взаимно перпендикулярных плоскостях геометрически суммируются.

286                                                                                                                       Лекция 35

Суммарный изгибающий момент: Ми  = √ Мx² + Мy² ;

М_и = √ 0, 9² + 0, 8² = 1, 2 кН • м.

Рассчитываем эквивалентный момент по теории максимальных касательных напряжений:

                   

  Условие прочности:           Мэкв

                                    σ _экв = --------- ≤ [σ ], Wосевое = Wх = Wу.

                                                    Wосевое

Момент сопротивления сечения: Woceeoe = 0, 1 • 60³ = 21600 мм³.

Проверяем прочность: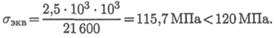

Прочность обеспечена.

Пример 2. Из условия прочности рассчитать необходимый диа­метр вала. На валу установлены два колеса. На колеса действуют две окружные силы Ft1 = 1, 2 кН; F_t2 = 2 кН   и  две   радиальные  силы  в  вертикальной  плоскости   F_r1 = 0, 43 кН; F_r2 = 0, 72 кН (рис. 35. 3). Диаметры колес соответственно равны d1 = 0, 1м; d2 = 0, 06м.

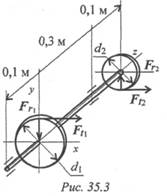Принять для материала вала [σ ] = 50МПа.

Рассчитать размеры вала кольце­вого сечения при с = 0, 8 (с =dВН/ d). Рас­чет провести по гипотезе максималь­ных касательных напряжений. Весом вала и колес пренебречь.

Решение

Указание. Используем прин­цип независимости действия сил, соста­вляем расчетные схемы вала в вертикальной и горизонтальной плоскостях. Определяем реакции в опорах в горизон­тальной и вертикальной плоскостях в отдельности. Строим эпюры изгибающих моментов (рис. 35. 4). Под действием окружных сил вал скручивается. Определяем действующий на валу крутящий момент.

                 Тема 2. 7. Расчет бруса круглого поперечного сечения                     287

 

Составим расчетную схему вала (рис. 35. 4).

1. Крутящий момент на валу:

    

 

2. Изгиб  рассматриваем   в   двух   плоскостях: горизонтальной (пл. Н)   и  вертикальной (пл. V).

В горизонтальной плоскости определяем реакции в опоре:

 

          

288                                                                                    Лекция 35

Определяем изгибающие моменты в точках С и В:

    Н                                                              Н

Мс = 400 • 0, 1 = 40Н • м; МВ = -2000 • 0, 1 = 200Н • м.

 

В вертикальной плоскости определяем реакции в опоре:                             

      

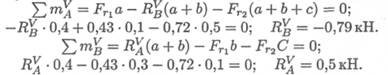
Определяем изгибающие моменты в точках С и В:

                          

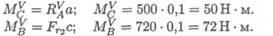
Суммарные изгибающие моменты в точках С и В:  

          

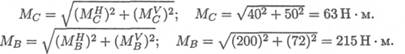
В точке В максимальный изгибающий момент, здесь же дей­ствует и крутящий момент.

Расчет диаметра вала ведем по наиболее нагруженному сечению.

3. Эквивалентный момент в точке В по третьей теории
прочности

                   

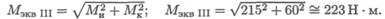
4. Определяем диаметр вала круглого поперечного сечения из
условия прочности

                

Округляем полученную величину: d — 36 мм.

Примечание. При выборе диаметров вала пользоваться стандартным рядом диаметров (Приложение 2).

5. Определяем необходимые размеры вала кольцевого сечения

                         dВН

при с = 0, 8; с = —, где d — наружный диаметр вала.

                          d

            

                    Тема 2. 7. Расчет бруса круглого поперечного сечения                 289

                

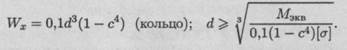
Диаметр вала кольцевого сечения можно определить по формуле

           

Примем   d = 42 мм.

Перегрузка незначительная. d_BH = 0, 8d = 0, 8 • 42 = 33, 6 мм.

Округляем до значения d_BH = 33 мм.

6. Сравним затраты металла по площадям сечения вала в обоих случаях.

Площадь поперечного сечения сплошного вала

                              

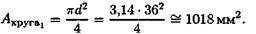
Площадь поперечного сечения полого вала

                 

Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения:

                

⇐ Предыдущая56575859606162636465Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: