 |
Примеры решения задач. Решение. 1. Гибкость стержня определяется по формуле . 2. Определяем минимальный радиус инерции для круга.
|
|
|
|
Примеры решения задач
Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37. 1.
Решение

1. Гибкость стержня определяется по формуле
λ = μ l / imin.
2. Определяем минимальный радиус инерции для круга.
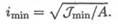
Тема 2. 10. Устойчивость сжатых стержней 297
Подставив выражения для Jmin и А (сечение — круг)
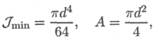
получим 
3. Коэффициент приведения длины для данной схемы крепления μ = 0, 5.
4. Гибкость стержня будет равна 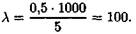
Пример 2. Как изменится критическая сила для стержня, если изменить способ закрепления концов? Сравнить представленные схемы (рис. 37. 2)

Решение

Критическая сила увеличится в 4 раза. FKP2 = 4FKPl.
Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37. 3а, двутавр № 12) заменить стержнем прямоугольного сечения той же площади (рис. 37. 3b)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.
298 Лекция 37
Решение

1. Определим ширину сечения прямоугольника, высота сечения
равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:
площадь сечения А1= 14, 7 см2;
минимальный из осевых моментов инерции Jy = 27, 9 см4.
По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.
|
|
|
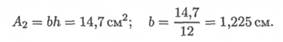
2. Определим минимальный из осевых моментов инерции.
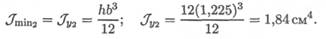
3. Критическая сила определяется по формуле Эйлера:

4. При прочих равных условиях отношение критических сил равно отношению минимальных моментов инерции:
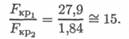
5. Таким образом, устойчивость стержня с сечением двутавр
№ 12 в 15 раз выше, чем устойчивость стержня выбранного прямоугольного сечения.
Тема 2. 10. Устойчивость сжатых стержней 299
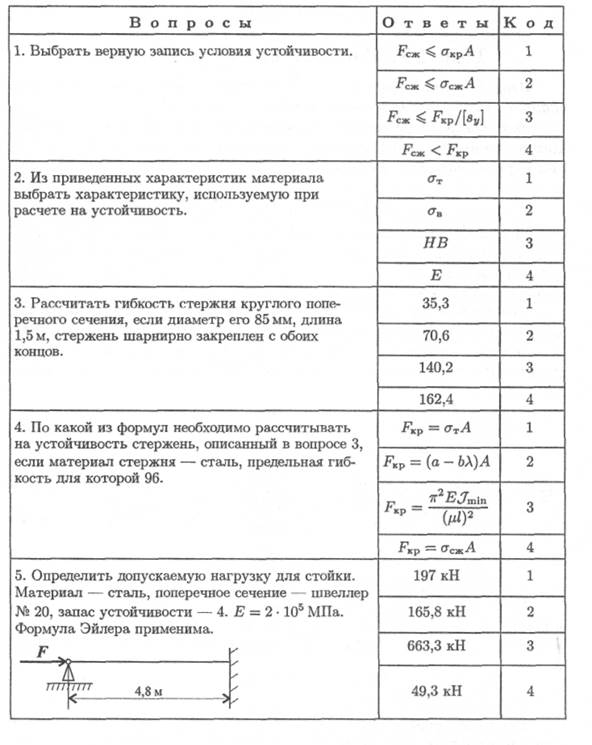
Пример 4. Проверить устойчивость стержня. Стержень длиной 1м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжимающей силой 82 кН (рис. 37. 4).
 Решение
Решение
1. Определяем основные геометрические пара метры сечения стержня по ГОСТ 8240-89.
Швеллер № 16: площадь сечения 18, 1см2; минимальный осевой момент сечения 63, 3 см4; минимальный радиус инерции сечения imin = 1, 87 см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала СтЗ λ пред = 100.
Расчетная гибкость стержня при длине l = 1м = 1000мм

Рассчитываемый стержень — стержень большой гибкости, расчет ведем по формуле Эйлера.

3. Допускаемая нагрузка на стержень [F] = FKp / [sy].

4. Условие устойчивости F ≤ [Fy];
82 кН < 105, 5 кН. Устойчивость стержня обеспечена.
300 Лекция 37
Тема 2. 10. Устойчивость сжатых стержней
 Тема 2. 8. Сопротивление усталости 301
Тема 2. 8. Сопротивление усталости 301
ЛЕКЦИЯ 38
Тема 2. 8. Сопротивление усталости
Иметь представление об усталости материалов, о кривой усталости и пределе выносливости.
|
|
|
Знать характер усталостных разрушений, факторы, влияющие на сопротивление усталости, основы расчета на прочность при переменном напряжении.
Основные понятия
Многие детали машин работают в условиях переменных во времени напряжений. Так, вращающиеся валы и оси, нагруженные постоянными изгибающими силами, работают при переменных нормальных напряжениях изгиба.
Совокупность последовательных значений переменных напряжений за один период процесса их изменения называется циклом.
Обычно цикл представляют в виде графика, в котором по оси абсцисс откладывается время, а по оси ординат — напряжения (рис. 38. 1).

Цикл характеризуется максимальным σ mах, минимальным σ тiп и средним напряжениями. Рассчитывается среднее значение напряжений σ т, амплитуда цикла σ а и коэффициент асимметрии цикла R

Все приведенные определения и соотношения можно записать и для касательных напряжений.
302 Лекция 38
Цикл, при котором максимальное и минимальное напряжения равны по величине и обратны по знаку, называют симметричным циклом (рис. 38. 2).

Остальные циклы называют асимметричными. Часто встречается отнулевой, или пульсирующий, цикл, минимальное напряжение при этом цикле равно нулю, среднее напряжение равно амплитуде (рис. 38. 3).
Переменные напряжения возникают в осях вагонов, рельсах, рессорах, валах машин, зубьях колес и многих других случаях.
Под действием переменных напряжений в материале возникает микротрещина, которая под действием повторяющихся напряжений растет в глубь изделия. Края трещины трутся друг о друга, и трещина быстро увеличивается. Поперечное сечение детали уменьшается, и в определенный момент случайный толчок или удар вызывает разрушение.
Появление трещин под действием переменных напряжений называют усталостным разрушением.
Усталостью называют процесс накопления повреждений в материале под действием повторно-переменных напряжений.
Характерный вид усталостных разрушений — трещины и часть поверхности блестящая в изломе. Такой характер излома вызван многократным нажатием, зашлифованностью частей детали.
|
|
|
Опыт показывает, что усталостное разрушение происходит при напряжениях ниже предела прочности, а часто и ниже предела текучести.
Способность материала противостоять усталостным разрушениям зависит от времени действия нагрузки и от цикла напряжений. При любой деформации нагружение с симметричным циклом наиболее опасно.
Тема 2. 8. Сопротивление усталости 303
Опытным путем установлено, что существует максимальное напряжение, при котором материал выдерживает, не разрушаясь значительное число циклов.
Наибольшее (максимальное) напряжение цикла, при котором не происходит усталостного разрушения образца из данного материала после любого большого числа циклов, называют пределом выносливости.
Для определения предела выносливости изготавливают серию одинаковых образцов и проводят испытания при симметричном цикле изгиба. Образцы имеют цилиндрическую форму, гладкую поверхность (полированную) и плавные переходы.
Образцы устанавливают на испытательную машину и нагружают так, чтобы напряжение составляло примерно 80% от предела прочности. После некоторого числа циклов образец разрушается. Фиксируют максимальное напряжение и число циклов до разрушения.
Испытания повторяют, постепенно снижая нагрузку на каждый последующий образец и фиксируя число циклов до разрушения образцов.
По результатам испытаний строят график зависимости между максимальным напряжением и числом циклов нагружений до разрушения. График называют кривой усталости (рис. 38. 4). В большинстве случаев после числа циклов нагружений более 107 кривая приближается к прямой, параллельной оси абсцисс.

п — число циклов нагружения;
σ R — предел выносливости:
σ -1 — предел выносливости при симметричном цикле (R = -1);
σ о — предел выносливости при от нулевом цикле (R = 0);
nбаз - число циклов, при котором определяют предел выносливости (базовое число циклов).
|
|
|
Если провести испытания при асимметричном цикле, кривая ляжет выше, т. е. выносливость материала повысится.
Предел выносливости, определенный путем стандартных испы-
304 Лекция 38
таний, является одной из механических характеристик материала.
|
|
|


