 |
Парный линейный и нелинейный регрессионный анализ
|
|
|
|
Парный линейный и нелинейный регрессионный анализ
Любую форму связи можно выразить уравнением общего вида y=f(x), где у – зависимая переменная (функция), а х – независимая переменная (аргумент).
Изменение зависимой переменной от одной или нескольких независимых называется регрессией. Известны эмпирические методы выравнивания (например, методом скользящей средней) и аналитические (линейное сглаживание и др. ).
Линейная регрессия
При одной независимой переменной и корреляции уравнение линейной регрессии имеет вид:
y=a0+a1x1 - прямая линия!
где y – ожидаемое значение функции,
а0 – свободный член в уравнении регрессии,
а1 – угловой коэффициент или коэффициент регрессии,
х1 – значение независимой переменной.
 |
Y
y=a0+a1x1
a1a1=rxy 
а0
׀ ׀ ׀ ׀ ׀
0 1 2 3 4 5 X1
Рис. 1. График прямолинейной регрессии
Нахождение уравнения линейной регрессии – это вычисление а0 и а1 на ПК. Оба этих параметра при корреляционной связи оцениваются с определенными статистическими ошибками, позволяющими установить значимость параметров а0 и а1.
Нелинейная регрессия
Полиномы второго и более высоких порядков
Уравнение прямой линии – частный случай полинома, это полином первой степени.
Полиномы больших степеней оказываются подчас лучше соответствующими исходным данным, и потому тоже используются.
Полином второй степени это квадратичная парабола
y=a0+a1x1 + a2x22.
В этом случае необходимо найти a0, a1 и a2 на ПК.
Прямая линия – частный случай квадратичной параболы, когда a2=0.
Y
Х
|
|
|
Рис. 2. Квадратичная парабола
В биологии, сельском и лесном хозяйствах квадратичная парабола обычно неплохо описывает связи: густота посева – урожайность, глубина заделки семян – урожайность и др. Во всех подобных случаях производственники должны найти оптимум фактора, обеспечивающего максимальную урожайность. Это так называемый поиск экстремума (рис. 2).
Парабола (полином ) третьего порядка описывается уравнением
y=a0+a1x1 + a2x22+ a3x33.
Она используется еще реже, а полиномы еще больших степеней в наших областях знаний практически не используются.
Гиперболы. Для аналитического сглаживания эмпирических рядов служат также гиперболы разных порядков с различным числом неизвестных.
Наиболее простая из них гипербола первого порядка вида:
В ряде случаев именно так изменяется загрязнение почвы продуктами выхлопных газов автомобилей при изменении расстояния от автотрассы – источника загрязнения.
Y
Х
Рис. 3. Гипербола первого порядка
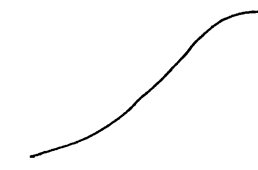
Регрессия, выражаемая уравнением логистической кривой
Логистическая кривая, называемая иногда S-образной, сигмоидной или кривой Сакса изображена на рис. 4.
Y
X
Рис. 4. Логистическая кривая
Описывается уравнением Ферхлюста, которое здесь не приводится. Такие кривые хорошо описывают изменения во времени (Х – время) высоты растений (в т. ч. деревьев), их массы, числа особей популяции в замкнутом пространстве и т. п. Эти кривые называют поэтому также кривыми роста.
Периодическая регрессия
Ее описывают обычно тригонометрическим уравнением регрессии, которое здесь не приводится.
Называют ее также циклической. Продолжительность периода (цикла) на рис. 5 обозначена буквой t.
|
|
|
В естественных популяциях периодически изменяется численность зайцев, рысей и ряда других животных. Периодически (с циклом в 14 лет) изменяется урожайность озимой пшеницы и ряда других с. -х. культур. Обнаружен вековой (~100-летний) цикл в динамике температуры и осадков на юго-востоке Украины.
В подобных случаях, когда независимой переменной является время (здесь годы), а зависимой какой-либо признак ряд называется рядом динамики или временным рядом.
t 
Анализ временных рядов производится с использованием парного корреляционного и регрессионного анализов так же, как это делают по любым парам других признаков.
Y
X (t)
Рис. 5. Периодическая кривая
В нашей программе REGAN предусмотрено аналитическое сглаживание следующими шестнадцатью функциями:
1. линейная,
2. периодическая
3. гипербола вида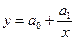 
4. степенная
5. показательная
6. экспоненциальная
7. логарифмическая
8. квадратичная парабола
9. логистическая
10. экспоненциальная вида y=a0× exp (a1× x2)
11. экспоненциальная видаy=a0× exp (a1× x4)
12. гипербола второго порядка
13. гипербола третьего порядка
14. гипербола первого порядка с тремя неизвестными
15. гипербола второго порядка с тремя неизвестными
16. гипербола третьего порядка с тремя неизвестными.
|
|
|
