2. Задачи для контрольных работ

2. ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ

2. 1. Физические основы механики

Кинематика

1. Определить модуль скорости материальной точки в момент времени  t = 2 c,  если точка движется по закону 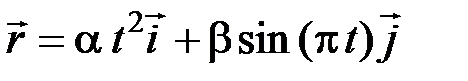,  где  a = 2 м/с² ;  b = 3 м.

2. Материальная точка движется по закону ,  где  a = 2 м;  b = 3 м.  Определить вектор скорости, вектор ускорения и траекторию движения материальной точки.

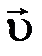3. Радиус-вектор частицы изменяется со временем по закону: (м).  Найти:  а) скорость   и ускорение   частицы;
б) модуль скорости  u  в момент  t = 1 c;  в) приближенное значение пути  S,  пройденного частицей за 11-ю секунду движения.

4. Частица движется со скоростью , где  a = 1 м/с².  Найти:  а) модуль скорости  u  частицы в момент времени t₁ = 2 c;  б) ускорение частицы   и его модуль;  в) путь  S,  пройденный частицей с момента  t₁ = 2 c  до момента  t₂ = 3 c.

5. Зависимость пройденного телом пути от времени задается уравнением  S = A + B t + C t² + D t³ (C = 0, 1 м/с²,  D = 0, 03 м/с³). Определить: 1) время после начала движения, через которое ускорение  а  тела будет равно 2 м/с²;  2) среднее ускорение  á аñ  тела за этот промежуток времени.

6. Тело брошено с высоты 25 м вертикально вверх со скоростью 20 м/с. Найти путь и среднюю скорость движения тела (до момента падения).

7. Звук выстрела и пуля одновременно достигают высоты 990 м. Выстрел произведён вертикально вверх. Определить начальную скорость пули. Средняя скорость звука в воздухе 330 м/с.

8. Вертолёт летит горизонтально со скоростью 40 м/с на высоте 45 м. С вертолета нужно сбросить груз на баржу, движущуюся в том же направлении со скоростью 2 м/с. На каком расстоянии, не долетев до баржи, летчик должен освободить крепеж груза?

9. Тело брошено вертикально вверх с начальной скоростью  u₀ = 4 м/с.  Когда оно достигло верхней точки полета, из того же начального пункта, с той же начальной скоростью  u₀  вертикально вверх брошено второе тело. На каком расстоянии  h  от начального пункта встретятся тела? Сопротивление воздуха не учитывать.

10. Материальная точка движется прямолинейно с ускорением а = 5 м/с².  Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять u₀ = 0.

11. Две автомашины движутся по дорогам, угол между которыми a = 60°. Скорости автомашин  u₁ = 54 км/ч  и  u₂ = 72 км/ч.  С какой скоростью  u  удаляются машины одна от другой?

12. Скорость течения реки  u = 3 км/ч,  а скорость движения лодки относительно воды  u₁ = 6 км/ч.  Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки.

13. Два электропоезда проследовали со скоростью 60 км/ч мимо
одной платформы в одном направлении с интервалом в 20 мин. С каким интервалом по времени их встретит поезд, идущий по встречной колее, если его скорость 72 км/ч?

14. Пловец переплывает реку по прямой, перпендикулярной берегу. Во сколько раз скорость пловца относительно воды больше скорости течения реки, если угол между векторами скорости пловца относительно воды и относительно берега равен 45°.

15. Материальная точка движется прямолинейно с начальной скоростью  u₀ = 10 м/с  и постоянным ускорением  a = 5 м/с².  Определить, во сколько раз путь  DS,  пройденный материальной точкой, будет превышать модуль ее перемещения  Dr  спустя  t = 4 c  после начала отсчета времени.

16. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью  u₁ = 8 км/ч.  Далее половину оставшегося времени он ехал со скоростью  u₂ = 22 км/ч,  после чего до конечного пункта он шел пешком со скоростью  u₃ = 5 км/ч.  Определить среднюю скорость  á añ  велосипедиста.

17. Камень, брошенный по льду со скоростью  u₀ = 5 м/с,  останавливается на расстоянии  S = 25 м  от места бросания. Определить путь, пройденный камнем за первые  t₁ = 2 c  движения.

18. Тело падает с высоты  h = 1 км  с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определите, какое время понадобится телу для прохождения:  1) первых 10 м пути;  2) последних 10 м
пути.

19. Тело, брошенное вертикально вверх, находилось на одной и той же высоте  h = 8, 6 м  два раза с интервалом  Dt = 3 с.  Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

20. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета.

21. С башни высотой H = 40 м брошено тело со скоростью u₀ = 20 м/с  под углом  a = 45°  к горизонту. Пренебрегая сопротивлением воздуха, определить:  1) время движения тела;  2) на каком расстоянии от основания башни тело упадет на землю;  3) скорость падения тела на землю;  4) угол, который составит траектория тела с горизонтом в точке его падения.

22. Мяч брошен с поверхности Земли со скоростью  u₀ = 10 м/с  под углом  a = 60°  к горизонту. Определить радиус кривизны его траектории в верхней точке подъема  R₁  и в момент падения на Землю  R₂.

23. Тело брошено под углом  a = 30°  к горизонту со скоростью  u₀ = 30 м/с.  Каковы будут нормальное  a_n  и тангенциальное  a_t  ускорения тела через время  t = 1 c  после начала движения?

24. Из пушки выпустили последовательно два снаряда со скоростью u₀ = 250 м/с:  первый под углом  j₁ = 60°  к горизонту, второй – под углом j₂ = 45° (азимут один и тот же). Найти интервал времени между снарядами, при котором снаряды столкнутся друг с другом.

25. Под каким углом к горизонту надо бросить шарик, чтобы радиус кривизны в начале его траектории был в  h = 8, 0 раз  больше, чем в вершине?

26. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Уравнение движения автомобиля  s = 10 + 10t - 0, 5t² (м). Найти скорость автомобиля, а также его тангенциальное, нормальное и полное ускорение в момент времени  t = 5 c.

27. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние между которыми 30 м. Пробоина во втором листе оказалась на 10 см ниже, чем в первом. Определить скорость пули, если к первому листу она подлетела, двигаясь горизонтально.

28. Мяч, брошенный горизонтально, ударяется о стенку, находящуюся на расстоянии 5 м от места бросания. Высота места удара мяча о стенку на 1 м меньше высоты, с которой был брошен мяч. С какой скоростью был брошен мяч? Под каким углом он подлетел к поверхности
стенки?

29. Два тела брошены одновременно из одной точки: одно – вертикально вверх, другое – под углом  a = 60°  к горизонту. Начальная скорость каждого тела 25 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через 1, 7 с.

30. Колесо вращается с постоянной скоростью, соответствующей 100 об. /мин. С некоторого момента колесо тормозится и вращается равнозамедленно с угловым ускорением 3 рад/с². Через какое время колесо остановится?

31. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали груз и предоставили ему
возможность опускаться. Двигаясь равноускоренно, груз за время  t = 3 с  опустился на  h = 1, 5 м.  Определить угловое ускорение e цилиндра, если его радиус  R = 4 см.

32. Минутная стрелка часов в 3 раза длиннее секундной. Найти соотношение между линейными скоростями концов этих стрелок.

33. Колесо радиусом R = 0, 1 м вращается так, что зависимость угловой скорости от времени задается уравнением  w = 2A t + 5B t (A = 2 рад/с², B = 1 рад/с⁵). Определить полное ускорение точек обода колеса через t = 1 с  после начала вращения и число оборотов, сделанных колесом за это время.

34. Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением a_n = A + B t + C t², A = 1 м/с², B = 6 м/с³, C = 3 м/с⁴.  Определить:  1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время  t₁ = 5 с  после начала движения; 3) полное ускорение для момента времени  t₂ = 1 с.

35. Частота вращения колеса при равнозамедленном движении за t = 1 мин уменьшилась от 300 до 180 с ^{– 1}. Определить:  1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.

36. Диск радиусом  R = 10 см  вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением  j = A + B t + C t² + D t³ (B = 1 рад/с, C = 1 рад/с², D = 1 рад/с³). Определить для точек на ободе колеса к концу второй секунды после начала движения:  1) тангенциальное ускорение  a_t;  2) нормальное ускорение  a_n;  3) полное ускорение  a.

37. Материальная точка движется по окружности с постоянной угловой скоростью  w = p / 6 рад/с.  Во сколько раз путь  Ds,  пройденный точкой за время  t = 4 с,  будет больше модуля ее перемещения  Dr?  Принять, что в момент начала отсчета времени радиус-вектор  r,  задающий положение точки на окружности, относительно исходного положения был повернут на угол  j₀ = p / 3 рад.

38. Материальная точка движется в плоскости  x y  согласно уравнениям:  x = A₁ + B₁ t + C₁ t²  и  y = A₂ + B₂ t + C₂ t²,  где  B₁ = 7 м/с, C₁ = 2 м/с², B₂ = – 1 м/с, C₂ = 0, 2 м/с². Найти модули скорости и ускорения точки в
момент времени  t = 5 c.

39. По краю равномерно вращающейся с угловой скоростью w = 1 рад/с платформы идет человек и обходит платформу за время t = 9, 9 с. Каково наибольшее ускорение  a  движения человека относительно Земли? Принять радиус платформы  R = 2 м.

40. Точка движется по окружности радиусом  R = 30 см  с постоянным угловым ускорением. Определить тангенциальное ускорение  a_t  точки, если известно, что за время  t = 4 с  она совершила три оборота и в конце третьего оборота ее нормальное ускорение  a_n = 2, 7 м/с².

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: