 |
Раздел 1. общие понятия и определения. свободные и вынужденные колебания механических систем.
|
|
|
|
Раздел 1. общие понятия и определения. свободные и вынужденные колебания механических систем.
1. 1. Свободные колебания механических систем
Любая механическая система содержит элементы упругости и массы. Если механическую систему вывести из состояния покоя, например, разовым импульсом силы, то она начинает совершать колебательное движение. В зависимости от характера распределения элементов массы и упругости механические системы можно подразделить на системы с сосредоточенными и распределенными постоянными.
Примером системы с сосредоточенными постоянными может служить масса, подвешенная на пружине или пружинный маятник. В этой системе элементы упругости и массы отделены один от другого (рис. 1. 1. ).
|
|
|
|
Рис. 1. 1 Простейшая механическая система с сосредоточенными постоянными |
| Рис. 1. 2. Простейшая механическая система с распределенными постоянными |
Для пояснения гармонических колебаний рассмотрим рис. 1. 3.
| |
Рис. 1. 3. График гармонических колебаний
В механической системе в процессе свободных колебаний внешние силы не приложены, система находится в динамическом равновесии под действием внутренних сил: инерционной и упругой.
Согласно второму закону Ньютона инерционная сила
(1. 1)
где m - масса,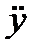 
- мгновенное значение колебательного ускорения.
Упругая сила
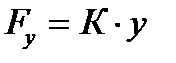, (1. 2)
где K - жесткость, y - мгновенное значение колебательного смещения.
Уравнение равновесия при свободных колебаниях имеет вид:
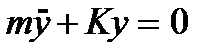, (1. 3)
|
|
|
Простейшая форма решения дифференциального уравнения (1. 3) - гармоническая функция от времени.
Чаще всего применяются две формы записи гармонической функции - синусоидальная и экспоненциальная
(1. 4)
(1. 5)
где 
- амплитудное значение смещения;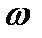 
- круговая частота, показывающая, какой угол в радианах пройдет радиус-вектор за единицу времени; t - время.
Важной характеристикой колебательного процесса является период колебаний Т - время одного колебания
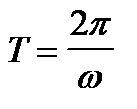, [c] (1. 6)
В акустике чаще применяется обратная величина - частота колебаний:
, [Гц] (1. 7)
Мгновенное значение колебательной скорости
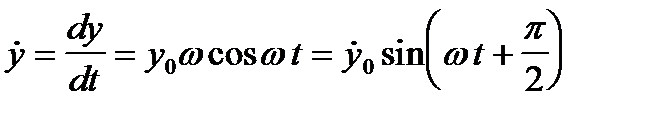(1. 8)
где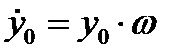 
- амплитуда колебательной скорости.
Из уравнений (1. 4), (1. 8) видно, что фаза колебательной скорости сдвинута относительно вектора колебательного смещения на угол p/2, то есть на 90°. Амплитуда скорости в 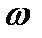раз больше амплитуды смещения.
Колебательное ускорение
(1. 9)
где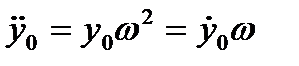 
амплитудное значение колебательного ускорения.
Численно амплитуда ускорения в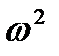 
раз больше амплитуды смещения и в 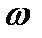раз больше амплитуды скорости. Знак минус в (1. 9) говорит о том, что фаза вектора ускорения сдвинута относительно вектора смещения на угол p или 180°, а относительно вектора скорости этот сдвиг составляет p/2 или 90о.
Подставим выражения (1. 4) и (1. 9) в (1. 3) откуда получим круговую частоту свободных колебаний
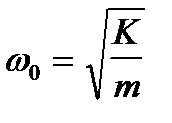(1. 10)
Линейная частота свободных колебаний
(1. 11)
|
|
|
Формула (1. 11) позволяет определять вертикальную частоту свободных колебаний (вдоль оси Z) механизма, установленного на амортизаторах. Реальные колебательные системы имеют шесть степеней свободы и, соответственно, шесть частот свободных колебаний - трех линейных 
по осям Х, У, Z и трех крутильных 
относительно осей X, Y, Z.
Принимая во внимание, что жесткость это физическая величина равная отношению силы, действующей на упругий элемент к деформации элемента под действием этой силы
[Н/м], (1. 12)
а для механизма, устанавливаемого на амортизаторы, эта сила есть сила тяжести F=mg, то с учетом (1. 11), (1. 12) получим:
(1. 13)
На практике в уравнение (1. 13) удобно подставить g = 981см/с2, тогда, частоту собственных колебаний можно определить по формуле
(1. 14)
где d - деформация упругого элемента в сантиметрах.
|
|
|
