 |
Резонанс наступает на частоте собственных колебаний системы, когда ее реактивное сопротивление равно нулю.
|
|
|
|
Резонанс наступает на частоте собственных колебаний системы, когда ее реактивное сопротивление равно нулю.
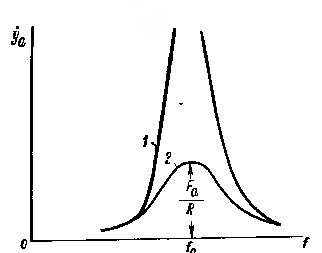
Рис. 1. 9
Так как для кругововой резонансной частоты ω 0 системы без трения справедливо:

Отсюда, резонансная частота системы без трения:
 (1. 34)
(1. 34)
частота такой системы получается равной частоте свободных колебаний системы. Частота резонансных колебаний в системе с трением несколько ниже частоты собственных колебаний в системе без трения; однако, в подавляющем большинстве случаев этим различием можно пренебречь.
На частоте резонанса системы её реактивное сопротивление равно нулю. Колебательная скорость массы из (1. 27):
 (1. 35)
(1. 35)
При отсутствии в системе сил трения колебательная скорость на резонансной частоте беспредельно увеличивается (кривая 1 на рис. 1. 9). Чем больше механические потери в системе, тем слабее выражен резонанс (кривая 2 на рис. 1. 9).
Примеры решения задач
Задача 1
Даны две колеблющиеся пластины. Частота колебаний первой пластины f1 = 20 Гц, амплитуда колебательного смещения ya1 = 0, 5 мм. Вторая пластина колеблется с частотой f2 = 1000 Гц и амплитудой ya2 = 0, 0005 мм. Определить колебательные ускорения обеих пластин.
Решение:
На основании формул (1. 7) и (1. 9) амплитуда колебательного ускорения первой пластины:
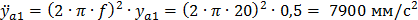
Колебательное ускорение второй пластины:

Ответ:  ;
; 
Задача 2
Механизм весом 2000 Н установлен на четырех пружинных амортизаторах. Каждый из них способен прогибаться на 1 мм под действием силы в 100 Н. Определить частоту собственных колебаний механизма на амортизаторах. Во сколько раз надо увеличить число амортизаторов, чтобы значение этой частоты удвоилось?
|
|
|
Решение:
Величину f0 можно найти по формуле (1. 10), выразив все величины в системе СИ.
Учитываем, что общая жесткость равна сумме жесткостей (упругостей).
Упругость каждого из амортизаторов:

Частота свободных колебаний амортизированного оборудования:
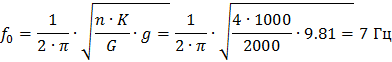
Для увеличения частоты в 2 раза, количество амортизаторов надо увеличить в 4 раза.
Ответ: 7 Гц, в 4 раза
Задача 3
В системе, изображенной на рис. 1. 1, вес груза равен 30 Н, а жесткость пружины 300 000 Н/м. Определить величину и характер механического сопротивления на частотах, лежащих на 20 Гц выше и ниже резонансной частоты.
Решение:
Резонансная частота системы из (1. 34):
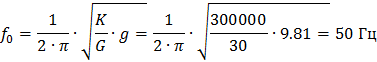
Величина механического сопротивления на частоте 70 Гц по (1. 30), (Н  с)/ м:
с)/ м:

Сопротивление системы на частотах выше резонансной имеет инерционный характер. Как было видно из уравнения (1. 30), инерционность системы отображается символом j перед значением сопротивления.
На частоте 30 Гц механическое сопротивление системы по (1. 30), (Н  с) / м:
с) / м:
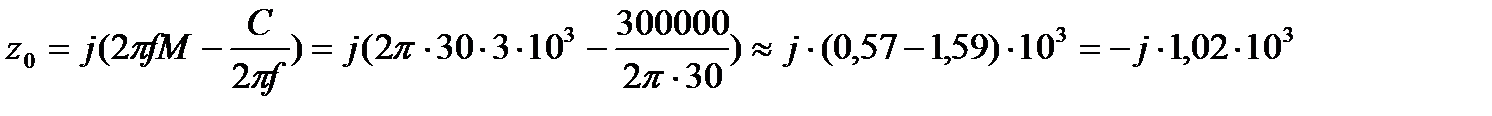
На частоте ниже резонанса сопротивление имеет упругий характер (символ – перед значением сопротивления, см. (1. 30)
Ответ: 

Задача 4
В систему, характеризуемую данными предыдущего примера, добавлен элемент трения. Сопротивление трения R = 100 (Н с)/м. Определить отношение амплитуды колебательной скорости системы при резонансе к амплитуде колебательной скорости на частоте 30 Гц.
Решение:
Так как сила трения невелика по сравнению с реактивными сопротивлениями, то резонансная частота системы не отличается заметно от частоты свободных колебаний системы без трения, а сопротивление системы на частоте 30 Гц практически равно её реактивному сопротивлению, т. е.:

Из формул (1. 28) и (1. 35) следует, что при постоянстве возмущающей силы отношение амплитуды колебательной скорости на резонансной частоте к амплитуде колебательной скорости на какой – либо другой частоте равно обратному отношению модулей механических сопротивлений системы на этих частотах. Механическое сопротивление системы на частоте резонанса определяется величиной трения (формула (1. 33)). Величина механического сопротивления системы на частоте 30 Гц была найдена в предыдущем примере. Взяв отношение этих величин, получим:
|
|
|

Амплитуда колебательной скорости на резонансе в 10 раз превышает амплитуду скорости на частоте, отличающейся от резонансной всего лишь на 20 Гц. Резкое возрастание скорости колебаний при резонансе объясняется относительно малой величиной трения в системе.
Ответ: в 10, 2 раза
|
|
|


