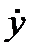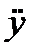|
1.2 Вынужденные колебания механических систем
|
|
|
|
|
|
Колебания механических систем называются вынужденными, если на систему действует внешняя периодическая возмущающая сила.
Напишем уравнение равновесия системы при вынужденных колебаниях с учетом сил трения. Силу трения считаем пропорциональной скорости колебательного движения.
Дифференциальное уравнение вынужденных колебаний запишется в виде:
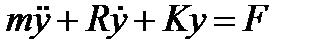 (1. 15)
(1. 15)
Периодическую возмущающую силу и колебательное смещение зададим в виде экспоненциальных функций
 (1. 16);
(1. 16);
 (1. 17);
(1. 17);
где  - амплитуда силы;
- амплитуда силы;
 - амплитуда перемещения;
- амплитуда перемещения;
е – основание натуральных логарифмов, е = 2, 718;
j = 
|
|
В основе этого метода лежит использование геометрической интерпретации комплексных чисел на комплексной плоскости (Рис. 1. 5).
Например, вектор А изображается в виде А=В+jС, где В, С - вещественная и мнимая составляющие вектора А.
Из рисунка 1. 5 видно, что:
 ,
,
где  - абсолютная величина или модуль комплексного числа А, j - фазовый угол
- абсолютная величина или модуль комплексного числа А, j - фазовый угол
Величина  (1. 17а)
(1. 17а)
Таким образом, вектор А может быть представлен в виде:

либо в виде:

Величину j называют оператором поворота фазы. Чтобы понять это название, продифференцируем дважды (1. 17):
Колебательная скорость
|
|
 (1. 18)
(1. 18)
где  (1. 19)
(1. 19)
| Рис. 1. 6. Векторная диаграмма колебательного процесса без трения |
|
|
|
Колебательное ускорение
 (1. 20)
(1. 20)
где  (1. 21)
(1. 21)
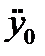 - амплитуда колебательного ускорения.
- амплитуда колебательного ускорения.
Умножение на j в (1. 20) показывает, что вектор колебательного ускорения повернут относительно вектора колебательной скорости на угол 90°, а относительно вектора колебательного смещения на угол 180°. При этом амплитуда вектора ускорения в w раз больше амплитуды вектора скорости и в w 2 раз больше амплитуды вектора смещения.
Общее решение уравнения (1. 15) содержит 2 члена: первый член соответствует свободным колебаниям системы, которые в данном случае являются затухающими, ввиду наличия трения; второй соответствует вынужденным колебаниям. Выраженгие колебательного смещения при вынужденных колебаниях может быть задано в виде формулы (1. 17). Подставив в формулу (1. 15) выражения смещения, скорости и ускорения из формул (1. 18) – (1. 21) и выражение F из формулы (1. 16), получим:
 (1. 22)
(1. 22)
то есть:

С учетом (1. 18) - (1. 21) перепишем (1. 22) в виде:

откуда
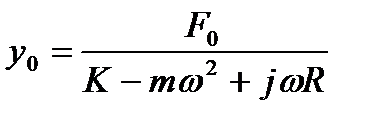 (1. 23)
(1. 23)
Для определения амплитуды колебательного смещения необходимо взять модуль комплексного выражения (1. 23). Тогда, на основании формулы (1. 17а) модуль равен:
 (1. 24)
(1. 24)
Теперь определим значение вектора и модуля амплитуды колебательной скорости. Ведь, именно колебательная скорость, а не колебательное смещение определяет величину энергии, излучаемой при колебаниях и степень звукоизоляции конструкций. Из формул (1. 18), (1. 20) следует
|
|
|
 (1. 25)
(1. 25)
После подстановки в формулу (1. 15), и сокращения 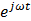 получаем:
получаем:
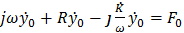 (1. 26)
(1. 26)
отсюда:
 (1. 27)
(1. 27)
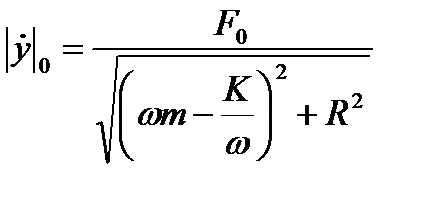 (1. 28)
(1. 28)
|
|
| Рис. 1. 7 |
Импеданс - есть физическая величина равная отношению возмущающей силы к колебательной скорости, вызванной воздействием этой силы
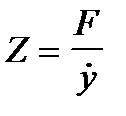 (1. 29)
(1. 29)
 (1. 30)
(1. 30)
Размерность механического сопротивления в системе СИ (Н  с)/м.
с)/м.
Рассмотрим три частных случая:
1. Колебательная система состоит из одной массы, т. е. К=0, R=0 (Пример: кусок пластилина, падающий на пол). Тогда из формулы (1. 30):
 (1. 31)
(1. 31)
Механическое сопротивление массы установившемуся колебательному движению пропорционально частоте колебаний. Таким образом, масса это фильтр высокочастотных колебаний.
2. Колебательная система обладает только упругостью, т. е. m =0, R=0 (Пример: стальная пружина в звукозаписывающей аппаратуре). Тогда из формулы (1. 30):
 (1. 32)
(1. 32)
Механическое сопротивление упругого элемента обратно пропорционально частоте колебаний.
3. Колебательная система обладает только внутренним трением, т. е. m =0, К=0 (Пример: гидравлический амортизатор, рессора). Тогда из формулы (1. 30):
 (1. 33)
(1. 33)
Механическое сопротивление элемента вязкого трения не зависит от частоты.
Из приведенных примеров, видно, что сопротивление массы и упругости откладываются по мнимой оси (первое – в положительном, а второе в отрицательном направлениях), а сопротивление трения – по вещественной оси.
| Рис. 1. 8. |
Графическая зависимость импеданса от частоты представлена на рис. 1. 8.
|
|
На рисунке обозначены Zm - инерционная составляющая импеданса, а Zk - жесткостная или упругая составляющая. При Zm = Zk в уравнении (1. 30) мнимая часть равна нулю (w m - K/w)=0 откуда определяется частота собственных колебаний 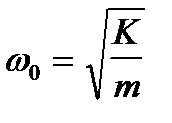 . Явление совпадения частоты собственных колебаний системы с частотой возмущающей силы называется резонансом. При резонансе импеданс принимает минимальное значение и численно равен активному сопротивлению R, которое откладывается по действительной оси. Сопротивления массы и упругости откладываются по мнимой оси (рис. 1. 8).
. Явление совпадения частоты собственных колебаний системы с частотой возмущающей силы называется резонансом. При резонансе импеданс принимает минимальное значение и численно равен активному сопротивлению R, которое откладывается по действительной оси. Сопротивления массы и упругости откладываются по мнимой оси (рис. 1. 8).
|
|
|
Умножение на j, как отмечалось выше, соответствует повороту фазы на 90°. Таким образом, сопротивление массы приводит к сдвигу фазы колебательной скорости относительно возмущающей силы на 90° в одну сторону, а сопротивление упругости - на 90° в другую сторону.
При действии только силы трения сдвиг фаз между силой и скоростью отсутствуют. Сопротивление трения, вызывающее необратимые потери колебательной энергии, называется активным сопротивлением.
Сопротивление массы и упругости не приводят к уменьшению колебательной энергии, а вызывают лишь сдвиг фазы между силой и скоростью. Эти сопротивления называются реактивными.
|
|
|