Уравнение прямой на плоскости, проходящей через две точки (с выводом).?

Пусть в пространстве заданы две точки M ₁ (x ₁, y ₁, z ₁) и M₂ (x ₂, y ₂, z ₂), тогда уравнение прямой, проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:

если х ₁ ≠ х₂ и х = х ₁, если х ₁ = х₂.

Дробь = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

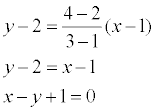
Общее уравнение прямой на плоскости и его исследование. Нормальный вектор прямой. Уравнение прямой «в отрезках» (с выводом).

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

 

Определение.

Нормальный вектор прямой - это любой ненулевой вектор, лежащий на любой прямой перпендикулярной данной.

Из определения нормального вектора прямой понятно, что существует бесконечное множество нормальных векторов данной прямой.

Пусть на плоскости задана прямоугольная декартова система координат Oxy. Одним из множества нормальных векторов координатной прямой Ox является координатный вектор . Действительно, вектор ненулевой и лежит на координатной прямой Oy, которая перпендикулярна оси Ox. Множество всех нормальных векторов координатной прямой Ox в прямоугольной системе координат Oxy можно задать как .

В прямоугольной системе координат Oxyz в трехмерном пространстве нормальным вектором прямой Oz является вектор . Координатный вектор также является нормальным вектором прямой Oz. Очевидно, что любой ненулевой вектор, лежащий в любой плоскости, перпендикулярной оси Oz, будет нормальным вектором прямой Oz.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или

, где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Условия коллинеарности векторов. Понятие направляющего вектора прямой. Каноническое уравнение прямой (с выводом).

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1.

Два вектора a и b коллинеарны, если существует число nтакое, что

a = n · b

Условия коллинеарности векторов 2.

Два вектора коллинеарны, если отношения их координат равны.

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

Условия коллинеарности векторов 3.

Два вектора коллинеарны, если их векторное произведениеравно нулевому вектору.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

 

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = {a_x; a_y; a_z} и b = {na_x; na_y; na_z}. Найдем их векторное произведение

a × b =	i	j	k	= i (aybz - azby) - j (axbz - azbx) + k (axby - aybx) =
ax	ay	az
bx	by	bz

= i (a_yna_z - a_zna_y) - j (a_xna_z - a_zna_x) + k (a_xna_y - a_yna_x) = 0 i + 0 j + 0 k = 0
Примеры задач на коллинеарность векторов

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: