Нормальное уравнение прямой на плоскости. Расстояние от точки прямой. Сделать чертеж.?

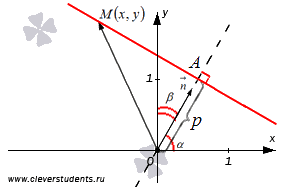
Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. Зададим прямую в этой системе координат, указав точку, через которую она проходит, и нормальный вектор прямой. В качестве нормального вектора нашей прямой возьмем вектор единичной длины , с началом в точке O. Его координаты равны соответственно и , где и - углы между вектором и положительными направлениями координатных осей Ox и Oy соответственно, то есть, . В качестве точки, через которую проходит прямая, возьмем точку А и будем считать, что она находится на расстоянии p единиц () от точки O в положительном направлении вектора (при p = 0 точка А совпадает с началом координат), то есть, .

Получим уравнение, которое задает эту прямую линию.

Очевидно, что точка лежит на рассматриваемой прямой тогда и только тогда, когда числовая проекция вектора на направление вектора равна p, то есть, при условии .

- радиус-вектор точки , следовательно, , что было показано в разделе координаты радиус-вектора точки. Тогда из определения скалярного произведения векторов мы получаем равенство , а это же скалярное произведение в координатной форме имеет вид . Следовательно, или . На этом вывод нормального уравнения прямой закончен.

Полученное уравнение вида называют нормальным уравнением прямой или нормированным уравнением прямой. Уравнение также называют уравнением прямой в нормальном виде.

Очевидно, нормальное уравнение прямой представляет собой общее уравнение прямой вида , в котором числа A и B таковы, что длина вектора равна единице, а число C неотрицательно.

Из вывода нормального уравнения прямой виден его геометрический смысл: нормальное уравнение прямой вида задает в прямоугольной системе координат Oxy на плоскости прямую с нормальным вектором единичной длины расположенную на расстоянии p единиц от начала координат в положительном направлении вектора .

Для примера приведем нормальное уравнение прямой . Оно в прямоугольной системе координат Oxy на плоскости задает прямую линию, нормальный вектор которой имеет координаты , и эта прямая удаленна от начала координат на 3 единицы в направлении, совпадающем с направлением нормального вектора .

Этот пункт статьи посвящен самому важному приложению нормального уравнения прямой – нахождению расстояния от заданной точки до заданной прямой на плоскости.

Обозначим расстояние от точки до прямой, заданной нормальным уравнением , буквой . Тогда расстояние может быть вычислено по формуле . То есть, для нахождения расстояния от точки до прямой следует подставить координаты заданной точки в левую часть нормального уравнения заданной прямой и взять абсолютную величину полученного значения. Вывод этой формулы показан в статье нахождение расстояния от точки до прямой. Там же дан альтернативный способ вычисления расстояния от точки до прямой на плоскости.

Приведем подробное решение примера.

Пример.

Найдите расстояние от точки до прямой, нормальное уравнение которой имеет вид .

Решение.

Из условия имеем . Воспользуемся формулой для вычисления расстояния от точки до прямой:

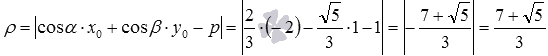
Ответ:

Пример.

Вычислите расстояние от точки 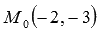до прямой .

Решение.

Приведем уравнение заданной прямой к нормальному виду. Для этого сначала получим общее уравнение прямой: 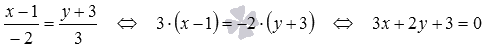. Вычислим нормирующий множитель . Умножим обе части общего уравнения прямой на нормирующий множитель: . Так мы получили нормальное уравнение прямой. Осталось для нахождения искомого расстояния подставить координаты заданной точки в левую часть нормального уравнения прямой и взять абсолютную величину: .

Ответ: