Уравнение прямой в пространстве, проходящей через две точки ( с выводом). ?

Прежде чем получить уравнение прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости, вспомним некоторые факты.

Одна из аксиом геометрии гласит, что через две несовпадающие точки на плоскости можно провести единственную прямую. Другими словами, задав две точки на плоскости, мы однозначно определяем прямую линию, которая через эти две точки проходит (при необходимости обращайтесь к разделу способы задания прямой на плоскости).

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy. В этой системе координат любой прямой линии соответствует некоторое уравнение прямой на плоскости. С этой же прямой неразрывно связан направляющий вектор прямой. Этих знаний вполне достаточно, чтобы составить уравнение прямой, проходящей через две заданные точки.

Сформулируем условие задачи: составить уравнение прямой a, которая в прямоугольной декартовой системе координат Oxy проходит через две несовпадающие точки и .

Покажем самое простое и универсальное решение этой задачи.

Нам известно, что каноническое уравнение прямой на плоскости вида задает в прямоугольной системе координат Oxy прямую линию, проходящую через точку и имеющую направляющий вектор .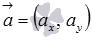

Напишем каноническое уравнение прямой a, проходящей через две заданные точки и .

Очевидно, направляющим вектором прямой a, которая проходит через точки М₁ и М₂, является вектор , он имеет координаты (при необходимости смотрите статью вычисление координат вектора по координатам точек его конца и начала). Таким образом, мы имеем все необходимые данные, чтобы написать каноническое уравнение прямой a – координаты ее направляющего вектора и координаты лежащей на ней точки (и ). Оно имеет вид 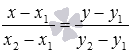(или ).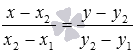

Также мы можем записать параметрические уравнения прямой на плоскости, проходящей через две точки и . Они имеют вид или .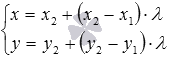

Разберем решение примера.

Пример.

Напишите уравнение прямой, которая проходит через две заданные точки .

Решение.

Мы выяснили, что каноническое уравнение прямой, проходящей через две точки с координатами и , имеет вид .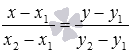

Из условия задачи имеем . Подставим эти данные в уравнение 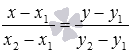. Получаем .

Ответ:

.

Если нам потребуется не каноническое уравнение прямой и не параметрические уравнения прямой, проходящей через две заданные точки, а уравнение прямой другого вида, то от канонического уравнения прямой всегда можно к нему прийти.

Пример.

Составьте общее уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через две точки и .

Решение.

Сначала напишем каноническое уравнение прямой, проходящей через две заданные точки. Оно имеет вид . Теперь приведем полученное уравнение к требуемому виду: .

Ответ:

.

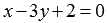На этом можно и закончить с уравнением прямой, проходящей через две заданные точки в прямоугольной системе координат на плоскости. Но хочется напомнить, как мы решали такую задачу в средней школе на уроках алгебры.

В школе нам было известно лишь уравнение прямой с угловым коэффициентом вида 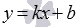. Найдем значение углового коэффициента k и числа b, при которых уравнение 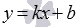определяет в прямоугольной системе координат Oxy на плоскости прямую линию, проходящую через точки и при . (Если же x₁=x₂, то угловой коэффициент прямой бесконечен, а прямую М₁М₂ определяет общее неполное уравнение прямой вида x-x₁=0).

Так как точки М₁ и М₂ лежат на прямой, то координаты этих точек удовлетворяют уравнению прямой 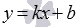, то есть, справедливы равенства и 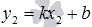. Решая систему уравнений вида относительно неизвестных переменных k и b, находим или . При этих значениях k и b уравнение прямой, проходящей через две точки и , принимает вид или .

Запоминать эти формулы не имеет смысла, при решении примеров проще повторять указанные действия.

Пример.

Напишите уравнение прямой с угловым коэффициентом, если эта прямая проходит через точки и .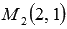

Решение.

В общем случае уравнение прямой с угловым коэффициентом имеет вид 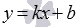. Найдем k и b, при которых уравнение 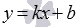соответствует прямой, проходящей через две точки и .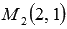

Так как точки М₁ и М₂ лежат на прямой, то их координаты удовлетворяют уравнению прямой 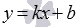, то есть, верны равенства и . Значения k и b находим как решение системы уравнений (при необходимости обращайтесь к статье решение систем линейных уравнений):

Осталось подставить найденные значения и в уравнение 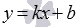. Таким образом, искомое уравнение прямой, проходящей через две точки и 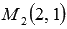, имеет вид .

Колоссальный труд, не так ли?

Намного проще записать каноническое уравнение прямой, проходящей через две точки и 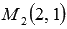, оно имеет вид , и от него перейти к уравнению прямой с угловым коэффициентом: .

Ответ:

.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: