Определение площади треугольника по заданным вершинам. Пример.?

Найти площадь треугольника, вершины которого находятся в точках A (2, -3), B (1, 1), C (-6, 5).

 

Решение.

Задачу очень просто решить, воспользовавшись формулой

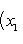
(1)

в которой нужно взять x ₁ = 2, x ₂ = 1, x ₃ = -6, y ₁ = -3, y ₂ = 1, y ₃ = 5.

Подставляя эти числа в (1), получим

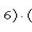
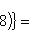
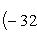
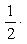
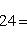
S = 12 кв. ед.

Понятие линейной комбинации матриц и пример ее определения.?

Линейной комбинацией (ЛК) строк матрицы называется выражение

ЛК называется тривиальной, если все коэффициенты равны нулю одновременно.

Пример

Замечание

Тривиальная ЛК равна нулевой строке.

Определение

ЛК называется нетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Пример

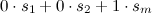
Замечание

Нетривиальная ЛК тоже может быть равной нулевой строке.

Пример

Определение

Система строк называется линейно зависимой (ЛЗ), если существует их нетривиальная ЛК, равная нулевой строке.

Пример

Система строк , линейно зависима, так как ЛК этих строк равна нулевой строке.

Определение

Система строк называется линейно независимой (ЛНЗ), если только тривиальная ЛК равна нулевой строке.

Пример

Задание. Показать, что система строк является ЛНЗ.

Решение. Составим ЛК заданных строк:

То есть ЛК данных строк равна нулевой строке, только если коэффициенты равны нулю одновременно.

Решение уравнений, содержащих неизвестную под знаком определителя.?

Пример

Задание. Вычислить определитель

Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ.

Решение неравенств, содержащих неизвестную под знаком определителя.?

Решить неравество 2 3х

>21.

−4 −5

Решение

Определитель второго порядка: a11=2, a12=3x, a21=−4 и a22=−5:

2 3x

−4 −5 = 2⋅(−5) −3x⋅(−4) = −10 + 12x.

Теперь заданное в условии неравенство станет таким: −10+12x>21. Отсюда следует, что 12x>31, x>31/12.

Ответ: x>31/12.

 

Вычисление угла между векторами, соединяющих данные точки. Пример.?

Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.

Решение: Найдем скалярное произведение векторов:

a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

|a| = √3² + 4² = √9 + 16 = √25 = 5
|b| = √4² + 3² = √16 + 9 = √25 = 5

Найдем угол между векторами:

cos α =	a · b	=		=		= 0.96
|a| · |b|	5 · 5

Составление общего уравнения прямой, проходящей через данную точку, с заданным направляющим вектором. Пример.?

р. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

х + у - 3 = 0

Составление общего уравнения прямой, проходящей через данную точку и параллельной другой прямой. Пример.?

Определение. Прямая, проходящая через точку М₁ (х₁, у₁) и перпендикулярная к прямой у = kx + b представляется уравнением:

Пример.

Напишите уравнение прямой, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 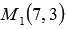параллельно прямой .

Решение.

Из параметрических уравнений прямой нам сразу видны координаты ее направляющего вектора . Этот вектор является направляющим вектором прямой, уравнение которой нам требуется составить. Уравнение прямой, проходящей через точку 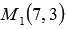и имеющей направляющий вектор с координатами , имеет вид .

Это и есть искомые уравнения прямой, проходящей через заданную точку 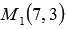параллельно заданной прямой .

Ответ:

⇐ Предыдущая567891011121314

Поделиться:

Воспользуйтесь поиском по сайту: