1.Множества, подмножества. Операции над множествами и их свойства. Диаграммы Эйлера – Венна

1. Множества, подмножества. Операции над множествами и их свойства. Диаграммы Эйлера – Венна

Множество – это совокупность объединенных по некоторым признакам различных объектов, называемых элементами множества. (Множества N натуральных чисел, Р – простых, Z - целых, К - вещественных )

Если объект х является элементом множества М, то говорят, что х принадле­ жит М. (х 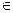М).

Множество, не содержащее элементов, называется пустым .

Обычно в конкретных рассуждениях элементы всех множеств берутся из неко­торого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсальным множеством (или универсумом).

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

перечислением элементов: М: ={a₁, a₂, ……, a_k}

характеристическим предикатом: М: = {х| Р(х)};

порождающей процедурой: М: = {x| x: = f}.

Характеристический предикат — это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадле­жит определяемому множеству, в противном случае — не принадлежит. Порождающая процедура — это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.

Два множества X и Y равны, т. е. , если они состоят из одних и тех же элементов.

Если каждый элемент x множества X,  является элементом множества Y, 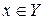, то X называется подмножеством множества Y, Y – надмножеством X ( ).

Мощность множества М обозначается как |M|. Для конечных множеств мощ­ность — это число элементов. Например, | | = 0, но |{ }| = 1.

Операции над множествами

Для двух множеств X и Y определяются следующие основные операции:

объединение: ;

пересечение: ;

разность:    ;

симметрическая разность: .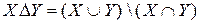

На рис. приведены диаграммы Эйлера, иллюстрирующие операции над мно­жествами.

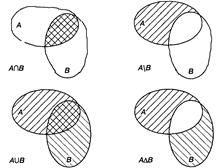
Свойства операций над множествами

Пусть задан универсум U. Тогда А, В, С  U выполняются следующие свойства

В справедливости перечисленных свойств можно убедиться различными спо­собами. Например, нарисовать диаграммы Эйлера для левой и правой частей равенства.

 

2. Покрытия и разбиения множеств. Биномиальные коэффициенты и числа Стирлинга второго рода. Перечисление элементов множеств.

Разбиения и покрытия

Пусть — некоторое семейство подмножеств множества

Семейство £ называется покрытием множества М, если каждый элемент М при­надлежит хотя бы одному из Ее

Семейство £ называется дизъюнктным, если элементы этого семейства попарно не пересекаются, то есть каждый элемент множества М принадлежит не более чем одному из множеств Ее

Дизъюнктное покрытие £ называется разбиением множества М.

Пример

Пусть М: ={1, 2, 3}. Тогда {{1, 2}, {2, 3}, {3, 1}} является покрытием, но не разби­ением; {{1}, {2}, {3}} является разбиением (и покрытием), а семейство {{1}, {2}} является дизъюнктным, но не является ни покрытием, ни разбиением.

Биномиальные коэффициенты

Число сочетаний С(m, n) — это число различных n-элементных подмножеств m-элементного множества. Числа С(m, n) встречаются в формулах решения многих комбинаторных задач.

Основная формула для числа сочетаний

позволяет получить следующие простые тождества.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: