 |
13. Подграфы. Остовные подграфы. Операции на графах.
|
|
|
|
Пример
Три внешне различные диаграммы являются диаграммами одного и того же графа
Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) — инварианты графа G.
Анализ графов на изоморфность целесообразно начинать со сравнениия значений их инвариантов. И только при их совпадении переходить к перебору допустимых вариантов нумерации вершин. Тривиальными инвариантами графа являются \V\ и \Е\. К числу инвариантов относится и степенная последовательность графа. Если, например, при совпадении степенных последовательностей двух графов в каждом из них есть одна вершина степени d, обозначенная в первом графе как v5 , то из всех возможных нумераций вершин второго графа следует рассмотреть только варианты, в которых вершина этой степени имеет такой же номер.
Существует множество других инвариантов, однако не известно системы инвариантов, позволяющей решать задачу изоморфизма для любых графов.
Пример
Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф. На рис представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны.
13. Подграфы. Остовные подграфы. Операции на графах.
Подграф H графа G – это граф H, содержащийся в графе G
Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и все рёбра, инцидентные данному подмножеству.
Остовы:
граф G = множество вершин P + множество рёбер Q.
Правило построения: существует подграф H такой, что V(H) = P, E(H) = Q 
двум вершинам V1, V2 из множества P соответствует (инцидентно) ребро из множества Q.
|
|
|
Подграф H графа G такой, что V(H) = V(G) – остов графа G. т. е.:
Остовом (неориентированного) связного графа G=(V, E) называется его частичный граф S=(V, T), являющийся деревом.
Операции на графах
Объединение графов.
Пусть G1(X1, E1) и G2(X2, E2) – произвольные графы. Объединением G1È G2 графов G1 и G2 называется граф с множеством вершин X1È X2, и с множеством ребер (дуг) E1È E2.
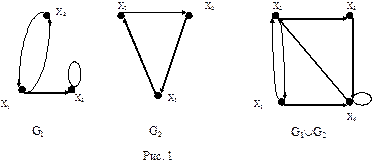
Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
G1È G2 = G2È G1 – свойство коммутативности;
G1È (G2È G3) = (G1È G2)È G3 – свойство ассоциативности.
Пересечение графов
Пусть G1(X1, E1) и G2(X2, E2) – произвольные графы. Пересечением G1Ç G2 графов G1 и G2 называется граф с множеством вершин X1Ç X2 с множеством ребер (дуг) E = E1Ç E2
Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
G1Ç G2 = G2Ç G1– свойство коммутативности;
G1Ç (G2Ç G3) = (G1Ç G2) Ç G3 – свойство ассоциативности.
Композиция графов
Пусть G1(X, E1) и G2(X, E2) — два графа с одним и тем же множеством вершин X. Композицией G1(G2) графов G1 и G2 называется граф с множеством вершин E, в котором существует дуга (xi, xj) тогда и только тогда, когда существует дуга (xi, xk), принадлежащая множеству E1, и дуга (xk, xj), принадлежащая множеству E2.
Декартово произведение графов. Пусть G1(X, E1) и G2(Y, E2) — два графа. Декартовым произведением G1(X, E1)´ G2(Y, E2) графов G1(X, E1) и G2(X, E2) называется граф с множеством вершин X´ Y, в котором дуга (ребро), идущая из вершины (xiyj) в (xkyl), существует тогда и только тогда когда существует дуга (xixk), принадлежащая множеству дуг E1 и j = l или когда существует дуга (yj, yl), принадлежащая множеству E2 и i = k.
Операция произведения графов. Пусть G1(X, E1) и G2(Y, E2) - два графа. Произведением G1× G2 графов G1 и G2 называется граф с множеством вершин X´ Y, а дуга из вершины (xi, yj) в вершину (xk, yl) существует тогда и только тогда, когда существуют дуги (xi, xk) Î E1 и (yj, yl) Î E2.
|
|
|
А также:
Удаление вершины v из графа G1(V1, E1) (обозначение G1(V1, E1)) — v, при условии v 
V1) дает граф G2(V2,. E2), где
Удаление ребра е из графа G1(V1, E1) (обозначение — G1(V1, E1) — е, при условии е E1 )дает граф G2(V2, E2), где
Добавление вершины v в граф G1(V1, E1) (обозначение —G1(V1, E1)). +-v, при условии v 
V1) дает граф G2{V2., E2), где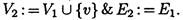 
Добавление ребра е в граф G1(V1, E1) (обозначение — G1(V1, E1)+e, при условии е . E1) дает граф , где G2(V2, E2), где 
Размножение вершины v графа G1(V1, E1) (обозначение — G1(V1, E1) ↑ v, при условии A 
V1, v Vi, v' V1) дает граф G2(V2, E2), где
|
|
|
