Бином Ньютона. 3.Представление множеств в ЭВМ. Коды Грея. Мультимножества. Алгоритм построения бинарного кода Грея. 4.Отношения и их основные свойства. Композиция отношений.

Бином Ньютона

Числа сочетаний С(m, n) называются также биномиальными коэффициентами Смысл этого названия устанавливается следующей теоремой, известной также как формула бинома Ньютона¹.

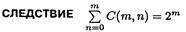
Свойства биномиальных коэффициентов

Из второй формулы вытекает эффективный способ реккурентного вычисления значений биномиальных коэффициентов, который можно предста­вить в графической форме, известной как треугольник Паскаля

В этом равнобедренном треугольнике каждое число (кроме 1 на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний C(m, n) находится в (m+1)-м ряду на (n+1)-м месте.

В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n-элементного множества на k непустых подмножеств.

S(n, n) = 1, для n ≥ 0,

S(n, 0) = 0, для n > 0,

 для 0 < k < n.

Следующие простые правила служат основными инструментами в теории перечислений элементов множеств:

правило равенства – при взаимно однозначном соответствии между элементами конечных множеств X и Y имеет место равенство ;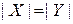

правило суммы – для любого разбиения конечного множества  имеет место равенство ;

правило произведения – для декартова произведения  семейства конечных множеств 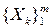 имеет место равенство .

3. Представление множеств в ЭВМ. Коды Грея. Мультимножества.

Задать представление какого-либо объ­екта (в данном случае множества) — значит описать в терминах используемой системы программирования структуру данных, используемую для хранения ин­формации о представляемом объекте, и алгоритмы над выбранными структура­ми данных, которые реализуют присущие данному объекту операции. Предполагается, что в используемой системе программирования доступны такие общеупотребительные структуры данных, как массивы, структуры (или записи) и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принад­лежности элементов множеству и описание алгоритмов для вычисления объеди­нения, пересечения и других введенных операций.

 

Алгоритм построения бинарного кода Грея

Данный алгоритм генерирует последовательность всех подмножеств п-элементного множества, причем каждое следующее подмножество получается из преды­дущего удалением или добавлением одного элемента.

Вход: п≥ 0 — мощность множества

Выход: последовательность кодов подмножеств В

i		В

 

Мультимножества. В множестве все элементы различны, а значит, входят в множество ровно 1 раз. В некоторых случаях оказывается полезным рассматривать совокупности элементов, в которые элементы входят по несколько раз.

Пример В штатном расписании одна и та же должность встречается несколько раз.

Пусть X = {x₁,..., х_п} — некоторое (конечное) множество и пусть а₁..., а_n — неотрицательные целые числа, Тогда мультимножеством (над множеством X) называется совокупность элементов множества X, в которую элемент x_i, входит a_i раз, a_i≥ 0. Мультимножество обозначается одним из следующих способов:

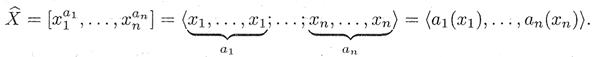
  ЗАМЕЧАНИЕ

Элементы мультимножества, равно как и элементы множества, считаются неупорядочен­ными.

 

4. Отношения и их основные свойства. Композиция отношений.

 

Прямым (декартовым) произведением двух множеств X и Y называется множество

,

где упорядоченная пара 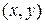 рассматривается как множество .

Степенью множества X называется множество

,

причем декартово произведение содержит n множителей.

По правилу произведения имеем: .

Бинарное отношение R из множества X в множество Y определяется как подмножество декартового произведения X и Y, т. е. выражением

,

что обычно описывается следующим образом:

.

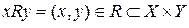Если , то говорят, что R есть отношение на множестве X. Для такого отношения вводятся следующие понятия:

обратное отношение:       ;

дополнение отношения:   ;

тождественное отношение: ;

универсальное отношение: .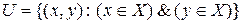

В соответствие с определением бинарного отношения n-арное отношение R определяется как множество упорядоченных n-арных наборов (кортежей)

.

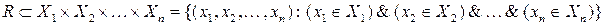Композицией двух отношений  и 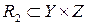 называется отношение 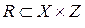, описываемое выражением

.

n-й степенью  отношения 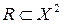 называется композиция n таких отношений, причем  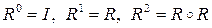и .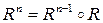

Справедливы следующие простые утверждения:

,

причем второе утверждение является следствием первого.

Отношение 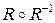 называется ядром отношения .

Отношение 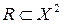 называется ( свойства отношений ):

рефлексивным          если ;

антирефлексивным, если ;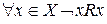

симметричным,         если ;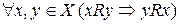

антисимметричным, если ;

транзитивным,          если ;

полным (линейным), если .

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: