 |
14. Компоненты графа, связность.
|
|
|
|
14. Компоненты графа, связность.
Связность. Две вершины в графе связаны, если существует соединяющая их (простая) цепь. (цепь – в следующем вопросе)
 Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует по крайней мере один путь.
Связный граф — граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует по крайней мере один путь.
Компонента связности графа — некоторое подмножество вершин графа такое, что для любых двух вершин из этого множества существует путь из одной в другую, и не существует пути из вершины этого множества в вершину не из этого множества.
Компонента сильной связности графа, слой — максимальное множество вершин ориентированного графа такое, что для любых двух вершин из этого множества существует путь как из первой во вторую, так и из второй в первую.
Связными компонентами графа называются подграфы данного графа, вершины которых являются классами эквивалентности отношения связности в данном графе.
15. Маршруты, цепи, циклы. Диаметр, радиус и обхват графа. Пути в орграфах.
Орграф, ориентированный граф G = (V, E) есть пара множеств, где V — множество вершин (узлов), E — множество дуг (ориентированных рёбер). Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v → w ведет от вершины v к вершине w, при этом вершина w смежная с вершиной v.
Маршрут – чередующаяся последовательность вершин и рёбер (для не орграфов). Если исходная и конечная вершины совпадают, маршрут называется циклическим.
Цепь – маршрут, у которого все рёбра различны.
Цикл – циклический маршрут-цепь.
Простая цепь (цикл) – цепь (цикл) у которого(-ой) все вершины различны.
|
|
|
Длина маршрута – число проходимых рёбер.
Расстояние между 2 вершинами – расстояние кратчайшей простой цепи. [d(v1, v2)]
Диаметр графа – 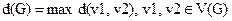
Обхват графа – длина произвольного кратчайшего простого цикла в графе. [girth(G)]
Для орграфа рассматривают ориентированные маршруты, цепи и циклы, проходящие согласно данной ориентации
Ориентированный цикл в орграфе = контур
Ориентированная цепь в орграфе = путь
В орграфе можно не принимать во внимание ориентацию
Путь в графе G = (V, E) — последовательность вершин  при
при 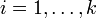 , таких, что две любые последовательные вершины соединены хотя бы одной дугой из E.
, таких, что две любые последовательные вершины соединены хотя бы одной дугой из E.
Число k вершин в пути называется его длиной. Каждая из пар двух последовательных вершин называется его звеном.
В орграфе зачастую этим термином называют не всякий, а только ориентированный путь, в котором у каждого из звеньев дуга идёт от вершины с меньшим номером к вершине с большим, т. е.:
Путь в орграфе — это последовательность вершин v1, v2, …, vn, для которой существуют дуги v1 → v2, v2 → v3, …, vn-1 → vn. Говорят, что этот путь начинается в вершине v1, проходит через вершины v2, v3, …, vn-1, и заканчивается в вершине vn.
| 
|
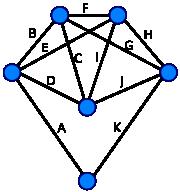
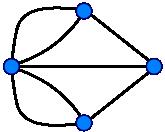
| Каждая вершина этого графа имеет чётную степень, поэтому этот граф — эйлеров. Обход рёбер в алфавитном порядке даёт эйлеров цикл. | Граф Кёнигсбергских мостов. Этот граф не является эйлеровым, поэтому решения не существует. |
Цепь / цикл, проходящая(-ий) через все рёбра графа (вершины могут повторяться) – эйлерова цепь (цикл)
Граф, имеющий эйлеров цикл – эйлеров граф. (т. е., граф, в котором существует цикл, содержащий все рёбра графа по одному разу (вершины могут повторяться))
16. Цикломатическое число и его свойства.
Определение: Цикломатическим числом графа(G) называется число связных компонент графа(p) плюс число рёбер минус число вершин

Пример: граф представлен множеством несвязных вершин. Тогда  =0,
=0, 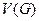 =p.
=p.  =0 -
=0 - 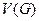 +
+ 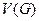 =0
=0
|
|
|
Свойство1: 
Свойство2:  - определяет число независимых циклов в графе. При
- определяет число независимых циклов в графе. При  равном нулю, граф не содержит циклов; если же оно равно единице, то граф имеет только один цикл.
равном нулю, граф не содержит циклов; если же оно равно единице, то граф имеет только один цикл.
Теорема: Цикломатическое число графа совпадает с максимальным числом независимых циклов этого графа. Максимальным числом независимых циклов называется - Базой
Док-во: Начнем с графа представленного изолированными вершинами и добавим по ребру.
Пусть имеется некоторая база 
 …. (*)
…. (*)
Добавим одно ребро => могут появиться новые циклы 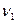
 …
…
Надо доказать что при добавлении ребра база циклов увеличивается на 1.
Оставшиеся циклы 
 … выражаем через предыдущие:
… выражаем через предыдущие:
 - m
- m 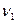 (1)(разность векторов циклов, м - некоторое число)
(1)(разность векторов циклов, м - некоторое число)
Тогда вектор (1) выраж. через базу(*). Т. е. максимальное число независимых циклов равно цикломатическому числу.
|
|
|


